Matematika_Praktikum

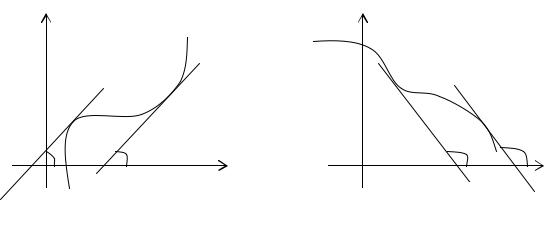
3.1. Промежутки монотонности и знакопостоянства

Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f / (x) 0.

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f /(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b] (рис. 3.1).

Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f /(x) 0 на этом отрезке. Если f (x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b] (рис. 3.2).

Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b). y y

	x		x

Рис. 3.1. Рис. 3.2.

3.2. Экстремумы функции

Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 + x) > f(x2) при любом х ( х может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

21

Точки максимума и минимума функции называются точками

экстремума.

(необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1

является точкой экстремума, то	производная функции
обращается в нуль в этой точке.

Но обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.

Пример: f(x) = x			Пример: f(x) = 3		х
	y		y

					x
	x
			Рис.		Рис. 3.4.
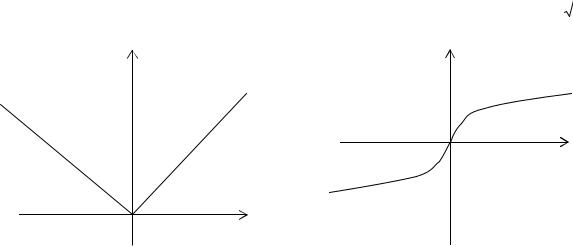
В точке х = 0 функция имеет				В точке х = 0 функция не
минимум, но не имеет				имеет ни максимума, ни
производной				минимума, ни производной

Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.

22

(Достаточные условия существования экстремума)

Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1).

Если при переходе через точку х1 слева направо производная функции f (x) меняет знак с “+” на “–“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “–“ на “+”, то функция имеет минимум.

Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:

1)Найти критические точки функции.

2)Найти значения функции в критических точках.

3)Найти значения функции на концах отрезка.

4)Выбрать среди полученных значений наибольшее и наименьшее.

3.3.Выпуклость и вогнутость функции. Точка перегиба

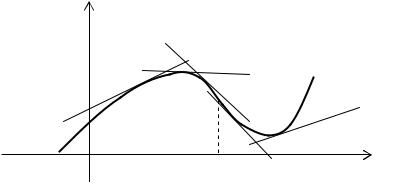
Опр. Кривая называется выпуклой на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая называется вогнутой на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале (рис. 3.5).

у

x

Рис. 3.5.

Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна (положительна), то кривая y = f(x) обращена выпукла (вогнута).

23

Точка, отделяющая выпуклую часть кривой от вогнутой,

называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Пусть кривая определяется уравнением y = f(x). Если вторая производная f (a) = 0 или f (a) не существует и при переходе через точку х = а меняет знак, то точка кривой с абсциссой х = а является

точкой перегиба.

3.4. Асимптоты

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты бывают вертикальные, наклонные и частный случай наклонных – горизонтальные.

Вертикальные асимптоты

Из определения асимптоты следует, что если lim f (x) или

x a 0

lim f (x) или lim f (x) , то прямая х = а – вертикальная

x a 0

x a

асимптота кривой y = f(x).

Наклонные и горизонтальные асимптоты

Наклонная асимптота задается уравнением прямой y = kx + b, где коэффициенты k и b вычисляются по следующим формулам:

k lim f (x) ,

x x

24

b lim f (x) kx

x

Если k =0, то получаем горизонтальную асимптоту.

3.5.Общая схема исследования функции и построение графиков

Графики функций строятся по точкам. Обычно из уравнения y=f(x) находят несколько точек графика функции y=f(x) и соединяют эти точки плавной кривой. Однако при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.

Для построения графика функции нужно исследовать ее свойства. Процесс исследования функции состоит из нескольких этапов.

1)Область определения функции.

2)Координаты точек пересечения с осями координат.

3)Четность, нечетность функции.

4)Асимптоты графика и пределы на ±∞. (Если они имеются).

5)Критические точки.

6)Интервалы монотонности и точки экстремума.

7)Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).

8)Дополнительные точки, если нет асимптот.

9)Построение графика.

10)Область значения функции.

3.6. Примеры

№1. Исследовать функцию на монотонность и экстремум

f( x) ( x 1)2( x 1)3 .

Решение.

25

1) D(f)=R

f'(x) 2(x 1)(x 1)3 3(x 1)2 (x 1)2 (x 1)(x 1)2 (5x 1)

2)5(x 1)(x 1)2 (x 1).

5

1

3) f '(x) 0 при x1 1, x2 5 , x3 1.

–1, 1 , 1 – критические точки, так как внутренние точки области

5

определения и f '(x) 0.

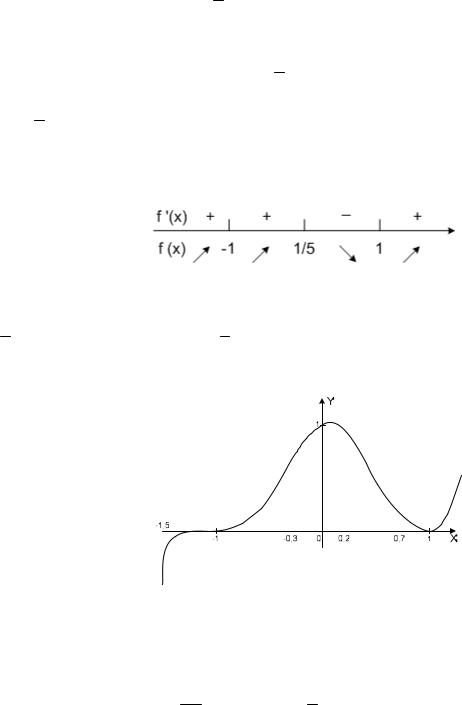
4) Выясним знаки производной:

Функция y=f(x) возрастает на промежутках (–∞; 1/5]; [1;+∞). Функция y=f(x) убывает на промежутке [1/5; 1].

1 – точка максимума, f(1 ) – максимум функции.

5

5

1 – точка минимума, f(1) – минимум функции (рис. 3.6.1).

Рис.3.6.

№2. Исследовать функцию на выпуклость и вогнутость. Найти

точки перегиба: y x3 2x2 3x 5 .

3 3

Решение.

1)D(f)=R

2)y'(x) x2 4x 3.

26

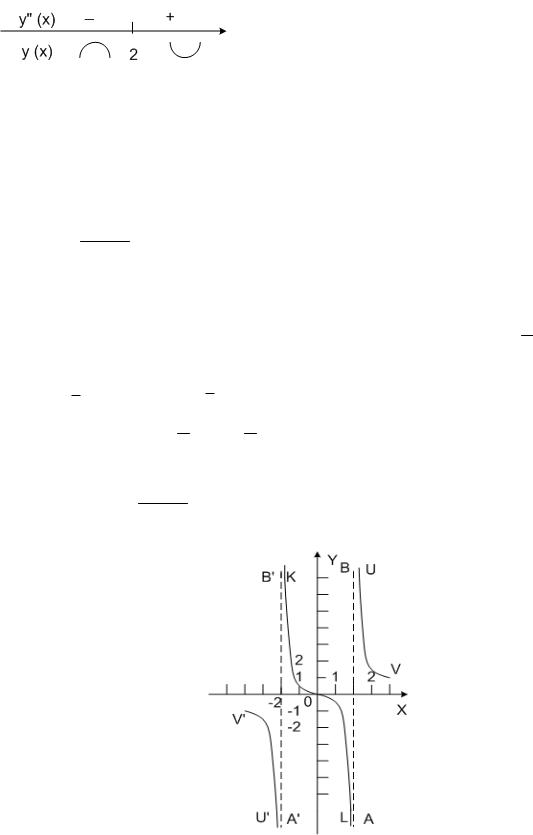
3) y (x) 2x 4 2(x 2).

y (x) 0 при x 2.

Функция y=f(x) выпуклая на промежутке (–∞; 2]. Функция y=f(x) вогнутая на промежутке [2; +∞). (2;–1) – точка перегиба.

№3. Найти вертикальные асимптоты линии:

а) y=tgx;

б) y 2x . x2 4

Решение.

а) Так как данная функция имеет разрыв в точках x= , то

2

lim tgx ,

x

2

lim tgx .

x

2

Следовательно, x , x – вертикальные асимптоты.

2 2

б) Функция 2x имеет бесконечный предел при х 2 и х -

x2 4

2.

Рис.3.7.

27

Значит, прямые х=2 и х= -2 (АВ и А′В′ на рис. 3.6.2) – асимптоты. Прямая АВ служит асимптотой для двух ветвей, UV и KL. Вдоль первой бесконечное удаление направлено вверх, вдоль

второй – вниз (ибо lim	2x		и lim	2x	. Аналогично
x 2 0 x2 4			x 2 0 x2 4

для прямой А′В′.

Заметим, что прямая х=0 служит горизонтальной асимптотой (для ветвей UV и U′V′).

	№4. Исследовать функцию y	x3		и построить ее график.
		x2 1

Решение.

1.Находим область определения функции: (– ; –1) (–1; 1) (1; ).

2.Точки пересечения с осью ОХ: у=0, тогда

	x3		0,
	x2 1

х=0, => (0; 0) – точка пересечения с осью ОХ. Точки пересечения с осью ОУ: х=0, тогда

y		03		0,
		2 1
0

у=0, => (0; 0) – точка пересечения с осью ОУ.

3. Область определения симметрична относительно нуля

	y( x)	( x)3			x3		y(x)
		( x)2 1			x2 1

Таким образом, функция является нечетной.

4.Так как точки х = 1, х = –1 являются точками разрыва, то вычислим следующие пределы:

28

lim

x2

;

1

x 1 0 x

2

lim

x2

;

1

x 1 0 x

2

lim

x2

;

x 1 0 x2

1

lim

x2

.

x 1 0 x2

1

Значит х = 1, х = –1 – вертикальные асимптоты.

Теперь найдем наклонные асимптоты.

k lim

x2

lim

1

1;

1

x x2

1

x

1

x2

1

x3

x3 x3 x

x

x

b lim

x

lim

lim

lim

0

x2 1

1

x x

2 1

x

x x2 1

x

1

x2

Итого, уравнение наклонной асимптоты – y = x. 5. Находим критические точки.

Найдем производную функции

y

3x2 (x2 1) 2x x3

3x4 3x2 2x4

x4 3x2

(x2 1)2

(x2 1)2

(x2 1)2

Критические точки: x = 0; x = –

; x =

; x = –1; x = 1.

3

3

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

x < – 3,						y > 0, функция возрастает
–			< x < –1,			y < 0, функция убывает
		3
–1 < x < 0,						y < 0, функция убывает
0	< x < 1,					y < 0, функция убывает
1	< x <				,	y < 0, функция убывает
				3
		< x,				y > 0, функция возрастает
	3

29

Видно, что точка х = –3 является точкой максимума, а точка

х =

3 является точкой минимума. Значения функции в этих

точках равны соответственно: –

3

3

и

3

3

.

2

2

6. Найдем вторую производную функции

y

(4x3 6x)(x2 1)2 (x4 3x2 )4x(x2 1)

(x2 1)4

(4x3 6x)(x4 2x2 1) (x4 3x2 )(4x3

4x)

(x2 1)4

4x7 8x5 4x3 6x5 12x3 6x 4x7 4x5 12x5 12x3

(x2 1)4

2x5

4x3 6x

2x(x4 2x2 3)

2x(x2 3)(x2 1)

2x(x2 3)

.

(x2 1)4

(x2 1)4

(x2 1)4

(x2 1)3

Определим выпуклость и вогнутость кривой на промежутках.

x < –1,	y < 0, кривая выпуклая
–1 < x < 0,	y > 0, кривая вогнутая
0 < x < 1,	y < 0, кривая выпуклая
1 < x,	y > 0, кривая вогнутая

–1, 0, 1 – точки перегиба.

7. Построим график функции:

		4
		3
		2
		1
-2	-1	1	2
		-1
		-2
		-3
		-4
		Рис. 3.8
		30