Рис. 13.2. Гистограмма распределения
13.1. Варианты заданий
№13.1.Через каждый час измерялось напряжение тока в электросети. При этом были получены следующие значения (В):
227 219 215 230 232 223 220 222 218 219 222 221 227 226 226 209
211 215 218 220 216 220 220 221 225 224 212 217 219 220.
Построить статистическое распределение и начертить полигон.
№13.2.Наблюдения за сахаром крови у 50 человек дали такие результаты:
3.943.84 3.86 4.06 3.67 3.97 3.76 3.61 3.96 4.04
3.823.94 3.98 3.57 3.87 4.07 3.99 3.69 3.76 3.71
3.813.71 4.16 3.76 4.00 3.46 4.08 3.88 4.01 3.93
3.923.89 4.02 4.17 3.72 4.09 3.78 4.02 3.73 3.52
3.913.62 4.18 4.26 4.03 4.14 3.72 4.33 3.82 4.03
Построить по этим данным интервальный вариационный ряд с
равными интервалами (I - 3.45-3.55; II - 3.55-3.65 и т. д.) и |
|
изобразить его графически, начертить гистограмму. |
|
№13.3.Построить полигон частот распределения скорости |
|
оседания эритроцитов (СОЭ) у 100 человек: |
|
|
xi |
1 |
3 |
5 |
7 |
9 |
ni |
10 |
15 |
30 |
33 |
12 |
171
№13.4.Построить гистограмму распределения скорости оседания эритроцитов (СОЭ) у 50 человек:
Интервал |
ni |
2-5 |
9 |
5-8 |
10 |
8-11 |
25 |
11-14 |
6 |
13.2. Статистические оценки параметров распределения. Выборочные характеристики
13.2.1. Характеристики положения
Мода (M0 ) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости или M0 =xi , такое, что n(xi ) = max.
Для одномодальных распределений мода – это наиболее часто
встречающаяся варианта в данной совокупности. |
|
Например, для распределения: |
|
|
|
xi |
16 |
|
17 |
18 |
20 |
ni |
5 |
|
1 |
20 |
6 |
M0 =18=x3 , так как n3 =20=max.
Для определения моды интервальных рядов служит формула:
|
|
|
|
n2 |
n1 |
|
|
M0 xíèæ |
x |
|
|
|
|
|
2n |
2 |
n n |
|
|
|
|
|
|
|
1 |
3 |
где xíèæ - нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости n2 ;n2 - частота модального интервала; n1 - частота интервала, предшествующего модальному; n3 - частота интервала, следующего за модальным;x - ширина интервала.
Определить моду ряда распределения кальция (мг %) в сыворотке крови обезьян.
Интерва |
8,6- |
9,4- |
10,2- |
11,0- |
11,8- |
12,6- |
13,4- |
14,2- |

лы |
|
|
9,3 |
|
|
10,1 |
|
|
10,9 |
11,7 |
12,5 |
|
13,3 |
|
14,1 |
14,9 |
Частота |
|
|
2 |
|
|
6 |
|
|
15 |
23 |
25 |
|
17 |
|
7 |
5 |
ni |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Частота модального класса n2 = 25, его нижняя |
граница |
|
xíèæ |
11,8. |
|
Частота |
класса, |
предшествующего |
модальному, n1 = 23; частота класса, следующего за модальным, |
n3 = 17; x |
= 0,8. Подставим эти данные в формулу, находим: |
|
|
|
|
|
|
25 23 |
|
|
|
|
|
|
|
|
|
|
M0 11,8 0,8 |
|
|
|
|
|
11,8 0,16 |
11,96. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,25 23 17 |
|
|
|
|
|
|
|
|
|
Найдите моду распределения роста 1000 взрослых мужчин: |
|
|
Рост, см |
|
|
Число |
Рост, см |
|
|
|
Число |
|
|
|
|
|
|
|
|
|
мужчин |
|
|
|
|
|
мужчин |
|
|
143-145 |
|
|
|
|
|
1 |
167-169 |
|
|
|
170 |
|
|
146-148 |
|
|
|
|
|
2 |
170-172 |
|
|
|
120 |
|
|
149-151 |
|
|
|
|
|
8 |
173-175 |
|
|
|
64 |
|
|
152-154 |
|
|
|
|
|
26 |
176-178 |
|
|
|
28 |
|
|
155-157 |
|
|
|
|
|
65 |
179-181 |
|
|
|
10 |
|
|
158-160 |
|
|
|
|
|
120 |
182-184 |
|
|
|
3 |
|
|
161-163 |
|
|
|
|
|
181 |
185-187 |
|
|
|
1 |
|
|
164-166 |
|
|
|
|
|
201 |
|
|
|
|
|
|
|
|
|
Решение: |
3(201 181) |
|
|
|
|
|
|
|
|
|
|
|
|
M0 164 |
|
164,21. |
|
|
|
|
|
|
|
|
|
2 201 181 170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Медиана Ме – это значение признака, относительно которого ряд распределения делится на 2 равные по объему части.
Например, в распределении: 12 14 16 18 20 22 24 26 28
медианой будет центральная варианта, т.е. Ме = 20, так как по обе стороны от нее отстоит по 4 варианты.
Для ряда с четным числом членов 6 8 10 12 14 16 18 20 22 24 медианой будет полусумма его центральных членов, т.е.
Me 14 16 15. 2

Выборочная средняя – это среднее арифметическое значение вариант статистического ряда
x1 k xini.
n i 1
xесть оценка математического ожидания случайной величины
по выборке.
В выборке взрослых мужчин n = 50 определяли содержание гемоглобина в крови. У n1=30 оно оказалось равным в среднем 70%. Для другой группы мужчин n2 = 20 этот показатель составил 50%. Найти среднюю арифметическую из этих двух средних.
Решение:
|
|
|
|
|
1 |
k |
|
x |
B |
|
xini ; |
|
|
|
По формуле: |
|
|
n i 1 |
|
x |
|
|
1 |
(30 70 20 50) 62% |
|
50 |
|
|
|
|
|
13.2.2. Характеристики рассеяния вариант вокруг своего среднего
Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения:
|
|
|
1 |
k |
Исправленная дисперсия при малых |
|
Dx |
|
(xi |
x |
B )2 ni. |
|
|
|
|
|
n i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
выборках n<30 Sx2 |
1 |
xi |
|
|
B |
ni |
|
x |
|
|
|
|
|
|
|
|
|
n 1 i 1 |
|
|
|
|
Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:
Sx 
 Sx2 – исправленное значение (n<30). x
Sx2 – исправленное значение (n<30). x 
 Dx Коэффициент вариации СV – это отношение среднего
Dx Коэффициент вариации СV – это отношение среднего
квадратического отклонения к средней величине признака, выраженное в процентах:
CV Sx 100%. xB
Коэффициент вариации – это мера относительной изменчивости случайной величины, которая позволяет сравнивать разнородные величины, например, частоту сердечных
20 15 10 5
сокращений (ЧСС, уд/мин), артериальное давление (АД, мм. рт. ст.) и температуру (t , C) в единых единицах - процентах.
Пример 4.
Выборочная совокупность задана таблицей распределения:
Найти выборочную дисперсию. Решение: Найдем выборочную среднюю:
20 1 15 2 10 3 5 4
xB 2.
Найдем выборочную дисперсию:
|
20(1 2) |
2 |
15(2 2) |
2 |
10(3 2) |
2 |
5(4 2) |
2 |
|
Dx |
|
|
|
|
1 |
|
|
20 15 10 5 |
|
|
|
|
|
|
|
|
|
|
Сравните 2 варьирующихся признака. Один характеризуется средней xi = 2,4 кг и средним квадратическим отклонением S1 = 0,58 кг, другой - величинами x2 = 8,3 см и S2 = 1,57 см. Какой признак варьируется сильнее?
Решение:
CV |
S1 |
100%, |
CV |
|
0,58 |
100% 24,2%, |
CV |
|
|
1,57 |
100% 18,9%. |
|
|
|
|
|
|
|
1 |
x |
|
1 |
2,4 |
|
|
2 |
8,3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Ответ: первый, так как CV1 |
CV2. . |
|
|
|
|
|
13.3. Варианты заданий
Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение, если совокупность задана таблицей распределения:
№ 13.1.
x1 |
1 |
|
|
4 |
8 |
ni |
5 |
|
|
3 |
2 |
№ 13.2. |
|
|
|
|
|
|
xi |
|
2 |
|
4 |
5 |
|
6 |
ni |
|
8 |
|
9 |
10 |
|
3 |
№ 13.3.
xi |
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
4 |
ni |
|
|
|
20 |
|
|
|
15 |
|
10 |
|
|
|
5 |
№ 13.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
7 |
ni |
8 |
|
7 |
|
16 |
|
10 |
|
6 |
|
2 |
|
1 |
№ 13.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
6,68 |
|
|
6,70 |
|
6,72 |
|
|
|
6,74 |
ni |
|
|
|
2 |
|
|
|
15 |
|
17 |
|
|
|
44 |
№ 13.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
6,76 |
|
6,78 |
|
6,80 |
|
6,82 |
|
|
6,84 |
ni |
|
|
|
52 |
|
44 |
|
14 |
|
11 |
|
|
1 |
13.4. Оценка параметров генеральной совокупности по ее выборке
Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема n, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах в целом.
Числовые значения, характеризующие генеральную совокупность, называются параметрами. Одна из задач математической статистики - определение параметров большого массива по исследованию его части.
Статистическое оценивание может выполняться двумя способами:
1)точечная оценка – оценка параметра, которая дается в виде одного числа (точки); 2)интервальная оценка – по данным выборки оценивается
интервал, в котором лежит истинное значение с заданной вероятностью.
176

13.4.1. Точечная оценка параметров генеральной совокупности
Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Это функция результатов выборки, и она является точечной оценкой генерального параметра, т. е. принимает только одно значение.
Качество оценки устанавливается по трем свойствам: быть состоятельной, эффективной и несмещенной.
Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.
Точечную оценку называют несмещенной, если ее
математическое ожидание равно оценивающему параметру при любом объеме выборки.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя xB :
xB 1 k xini ,
n i 1
где xi - варианты выборки; ni - частота встречаемости вариант xi ; n - объем выборки.
Выборочная средняя является несмещенной оценкой генеральной средней, так как M(xB ) xãåí ,т.е. она эквивалентна истинной средней в генеральной совокупности (популяции).
Выборочная дисперсия SB2 не обладает свойством несмещенности. Это смещенная оценка генеральной дисперсии
ãåí2 .
M(S2 ) n 1 2 2 - это и означает, что выборочная дисперсия S2
b n ãåí ãåí b
является смещенной оценкой ãåí2 На практике используют исправленную выборочную дисперсию
Sb2 , которая является несмещенной оценкой дисперсии генеральной совокупности:
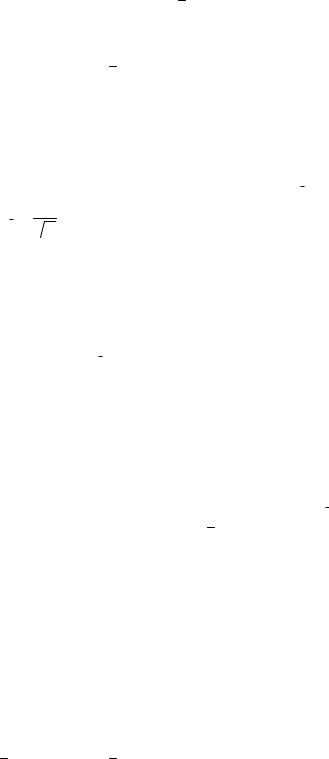
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
S2 |
|
n |
|
Sb2 |
n |
|
(xi |
|
x |
b )2 ni |
|
i 1 |
|
|
|
; |
n 1 |
n 1 |
|
|
|
|
|
|
n |
|
|
1 |
|
k |
|
|
|
|
|
|
|
|
|
S2 |
|
|
(xi |
|
x |
b )2 ni. |
|
|
|
|
|
|
|
|
|
|
|
|
n 1 i 1 |
|
|
|
|
|
|
|
|
|
Кроме того, в расчетах используют S - исправленное среднее квадратическое отклонение, называемое стандартным отклонением в выборке и ошибку выборочной средней (стандартную ошибку средней) mx :
mx S ,которая отражает точность оценки.
 n
n
Стандартная ошибка уменьшится, т. е. оценка станет более точной, если объем выборки n увеличится и данные имеют небольшое рассеяние S.
Рассмотрим разницу между S - стандартным отклонением в выборке и mx - стандартной ошибкой среднего.
На первый взгляд, они очень схожи, но их используют в разных целях. Среднее квадратическое отклонение S отражает вариабельность в значениях данных, и его указывают, если надо пояснить изменчивость в наборе данных, разброс данных.
Ошибка выборочной средней mx характеризует точность выборочного среднего xb и должна быть указана, если интерес представляет среднее значение выборки.
Из генеральной совокупности извлечена выборка объема n=50.
xi |
2 |
5 |
10 |
7 |
ni |
16 |
12 |
8 |
14 |
Найти несмещенную оценку генеральной средней.
Решение:
|
|
|
|
1 |
k |
|
|
|
16 2 5 12 7 8 10 14 |
|
|
x |
b |
|
xini ; |
x |
b |
|
5,76. |
|
|
|
|
|
|
|
n i 1 |
|
|
50 |
|
По выборке объема 30 найдена смещенная оценка Sb2 = 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение:

Эта несмещенная оценка равна исправленной дисперсии:
|
S2 |
n |
|
S2 |
, |
S2 |
30 |
3 3,1. |
|
n 1 |
29 |
|
|
b |
|
|
|
Найти несмещенную оценку генеральной средней, дисперсии генеральной совокупности и стандартное отклонение по выборке объема 12, описывающую продолжительность в секундах физической нагрузки до развития приступа стенокардии:
289,203,359,243,232,210,251,251,246,224,239,220,211.
Решение:
|
x |
b |
|
289 203 ... 211 |
244; |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
S2 |
|
|
1 |
|
(289 244)2 (203 244)2 |
... (211 244)2 1849; |
|
11 |
|
|
|
|
|
|
|
|
S2 |
1849; |
|
|
S 43. |
|
|
|
13.5. Варианты заданий
№13.1. При исследовании клинической оценки тяжести серповидноклеточной анемии была получена выборка объема 33. 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 4; 4; 5; 5;5;5;6;7;9;10;11.
Найдите среднюю, среднее квадртическое отклонение и медиану. Можно ли считать, что выборка извлечена из совокупности с нормальным распределением?
№13.2. Исследуя продолжительность (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца, получили следующие данные:
289;203; 359; 243; 232; 210; 215; 246; 224; 239; 220; 211. Найдите среднюю, среднее квадратическое отклонение, медиану. Можно ли считать, что данная выборка извлечена из совокупности с нормальным распределением?
№13.3. Найдите среднее число очков, выпадающих при бросании игральной кости. Опишите это распределение. Может ли оно быть нормальным?
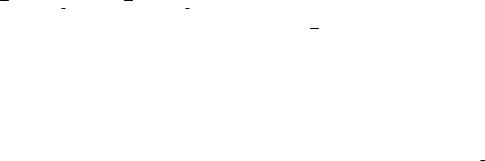
13.6. Интервальная оценка параметров генеральной совокупности
Точечные оценки параметров распределения не дают информации о степени близости к соответствующему теоретическому параметру. Поэтому построение интервала, в котором с заданной степенью достоверности будет находиться оцениваемый параметр, является более информативным способом оценивания неизвестных параметров.
Интервальная оценка – это числовой интервал, который определяется двумя числами-границами интервала, содержащий неизвестный параметр генеральной совокупности.
Доверительный интервал – это интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности.
Доверительная вероятность р - это такая вероятность, что
событие |
вероятности |
(1 - р) можно считать невозможным. |
1 p- |
это уровень |
значимости. (Обозначения могут быть |
любыми, часто обозначают наоборот). Обычно в качестве доверительных вероятностей используют вероятности, близкие к 1. Тогда событие, что интервал накроет характеристику, будет практически достоверным. Это p 0,95, p 0,99, p 0,999.
Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей. Обычно указывают 95% доверительный интервал.
Для выборки малого объема (n< 30) нормально распределенного количественного признака х доверительный интервал может иметь вид:
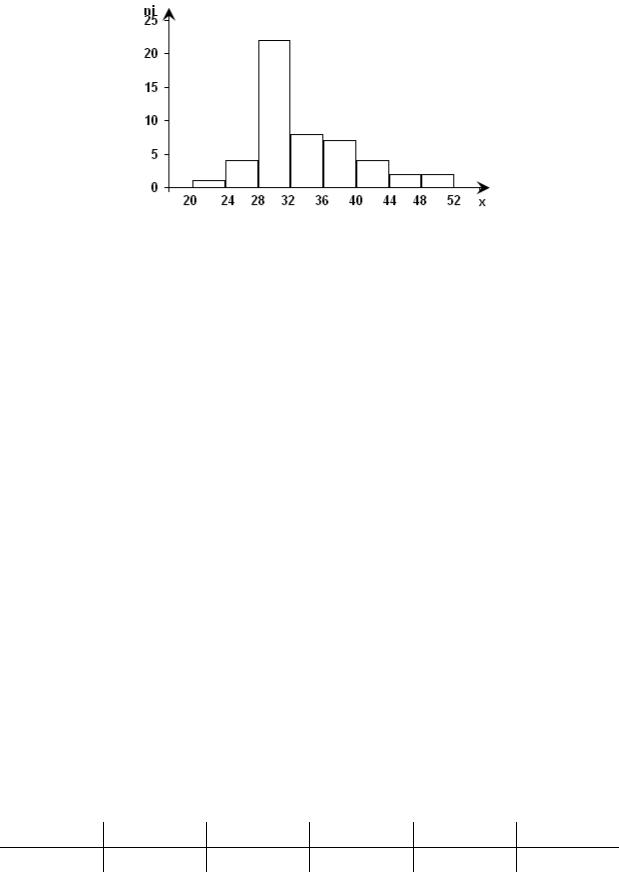
xB (mx )t xB (mx )t (p 0,95),
где | - генеральное среднее; xB - выборочное среднее; t - нормированный показатель распределения Стъюдента с (n - 1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал. Термин «степени свободы» означает, что их можно вычислить как объем выборки минус число ограничивающих условий; (mx ) — ошибка выборочной средней.





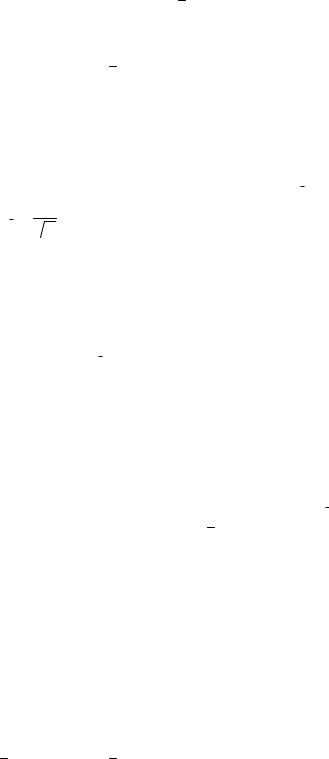






 n
n