Matematika_Praktikum

Решение:

( x

) ( y

)

r

x

y

.

( x

)2 ( y

)2

x

y

Средний рост

:

x

x ,

31 32 ... 46

369

36,9.

x

x

n

10

10

Средняя масса

:

y

y ,

7,8 8,3 ... 13,0

10,38.

y

y

n

10

Находим:

( x x) ( y y) (31 36,9) (7,8 10,38) ... (46 36,9) (13 10,38) 99,9;

(x x)2 (31 36,9)2 (32 36,9)2 ... (46 36,9)2 224,8;

( y y)2 (7,8 10,38)2 (8,3 10,38)2 ... (13,0 10,38)2 51,9.

Подставим полученные значения в формулу для r:

99,9

r 0,925.

224,8 51,9

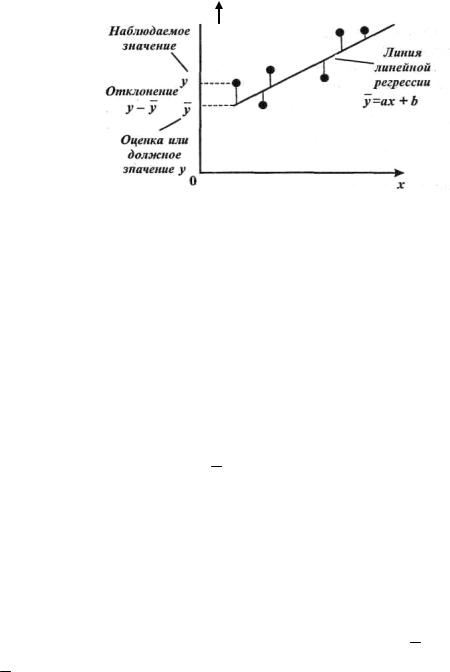
Величина r близка к 1, это говорит о тесной связи роста и массы.

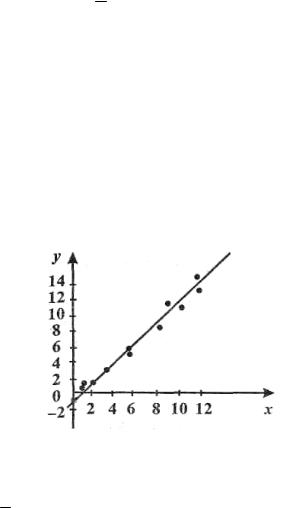
Построить корреляционное поле точек и найти коэффициент корреляции между производительностью труда Y (тыс. руб.) и энерговооруженностью труда X (кВт) (в расчете на одного рабочего) для 14 предприятий региона по следующим данным:

xi 2,8 2,2 3,0 3,5 3,2 3,7 4,0 4,8 6,0 5,4 5,2 5,4 6,0 9,0

yi 6,7 6,9 7,2 7,3 8,4 8,8 9,1 9,8 10,6 10,7 11,1 11,8 12,1 12,4

Решение:

x x , x 2,8 2,2 ... 9,0 64,2 4,6.

n

14

14

y y , y 6,7... 12,0 9,5.

n14

( x x) ( y y) (2,8 4,6) (6,7 9,5) ... 41,55.

(x x)2 (2,8 4,6)2 (2,2 4,6)2 ... 40,8.

191

( y y)2 (6,7 9,5)2 (6,9 9,5)2 ... 52,35.

Подставим в формулу для r:

		( x x ) ( y y )
r								0,898,
		( x		)2 ( y		)2
			x		y

что говорит о тесной связи между переменными.

14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции

Это ответ на вопрос: существует ли вообще эта связь. Эмпирический коэффициент корреляции, как и любой

другой выборочный показатель, служит оценкой своего генерального параметра. Выборочный коэффициент линейной корреляции rв - величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина, имеет ошибку тr.

Чтобы выяснить, находятся ли случайные величины X и Y генеральной совокупности в линейной корреляционной зависимости, надо проверить значимость rв. Для этого проверяют нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности H0: rген = 0, то есть линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза H1: rген ≠ 0, то есть эта линейная корреляционная связь имеется. Задается уровень значимости, например, α ≤ 0,05.

Критерием для проверки нулевой гипотезы является отношение выборочного коэффициента корреляции к своей ошибке:

r

tнабл mr ,

где тr - ошибка коэффициента корреляции.

Если объем выборки п < 100, то mr 1 r2 ;;

n 2

если объем выборки п > 100, то mr 1 r2 .

n

192

Число степеней свободы для проверки критерия равно f = п - 2. Гипотезу проверяют по таблицам распределения Стьюдента в соответствии с выбранным уровнем значимости.

По таблице критических точек распределения Стьюдента находим tкрит (α, f), определенное на уровне значимости α ≤ 0,05 при числе степеней свободы f = п - 2, где n - объем двумерной выборки.

Если tнабл > tкрит => H1 - отвергают нулевую гипотезу и принимают альтернативную: rген ≠ 0, имеется линейная корреляционная связь между признаками.

Если tнабл < tкрит - то нет оснований отвергать нулевую гипотезу, а rв статистически незначим. Эта связь случайна.

Проверить значимость коэффициента корреляции r = 0,74 между переменными X и Y для выборки объема n = 50.

Решение:

Проверяется нулевая гипотеза H0 об отсутствии линейной корреляционной связи между переменными X и Y в генеральной совокупности H0: rген = 0.

При справедливости этой гипотезы

tнабл

r

, где ошибка

mr

1 r2

r

коэффициента корреляции mr

и

tнабл

n 2

имеют

1 r2

n 2

распределение Стьюдента сf = n-2 степенями свободы.

	Рассчитаем: tнабл	0,74		50 2		7,62..
			1 0,742

По таблицам находим табличное значение t-критерия Стьюдента, определенное на уровне значимости α ≤ 0,05 и при

числе степеней свободы f = 50 - 2 = 48, tкрит(α ≤ 0,05; 48) = 2,02.

Поскольку tнабл > tкрит, 7,62 > 2,02, коэффициент корреляции значимо отличается от нуля.

Причем это справедливо и для уровня значимости: α ≤ 0,001 (t = 3,55).

193

По выборке объема п = 122, извлеченной из нормальной двумерной совокупности (X, Y), найден выборочный коэффициент линейной корреляции r = 0,4. При уровне значимости α ≤ 0,05 проверить нулевую гипотезу H0, которая заключается в том, что связь между признаками случайна.

Решение:

H0 : rген 0,	H1 : rген					0,	0,05,				tкрит 1,98,
		r						0,4				0,4 11
f 120, tнабл			n		,	tнабл			1221				5,24.
		1 r2						1 0,16				0,84

Сравниваем: tнабл > tкрит (α, f), 5,24 > 1,98 => H1 – отвергается нулевая гипотеза.

Вывод: имеется умеренная линейная корреляционная связь между признаками: r = 0,4 (α ≤ 0,05).

14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов

При проведении современных клинических исследований обычно нет недостатка в информации: каждому пациенту соответствует целое множество различных клинических показателей и данных.

В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа.

При этом задача регрессионного анализа состоит в подборе упрощенной аппроксимации этой связи с помощью математической модели.

Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватной для описания имеющихся данных.

Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных.

Выше указывалось, что результаты наблюдений,

приведенные в двумерной выборке:
xi	x1	x2	x3	x4	x5

194

yi

y1

y2

y3

y4

y5

можно представить в виде корреляционного поля точек (рис. 14.3), где каждая точка соответствует отдельным значениям х и у.

Рис. 14.3. Метод наименьших квадратов

Врезультате получается диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками. Довольно часто эта связь может быть аппроксимирована прямой линией (рис. 14.3).

Регрессия - это функция, позволяющая по величине одного признака X находить среднее ожидаемое (должное) значение другого признака Y, корреляционно связанного с X.

Влинейной математической модели уравнение линейной регрессии имеет вид:

y ax b,

где а и b - параметры линейной регрессии;

а - это коэффициент регрессии, показывающий, насколько в среднем величина одного признака Y изменяется при изменении на единицу меры другого признака X, корреляционно связанного с Y. Чем больше a - угловой коэффициент прямой а= tg α, тем круче прямая, то есть быстрее изменяется Y.

b - свободный член в уравнении, определяет y; при x = 0.

y - это предсказанное (должное) значение Y для данного х при определенных значениях регрессионных параметров.

Параметры линейной регрессии определяют методом наименьших квадратов - это способ подбора параметров регрессионной модели, согласно которому сумма квадратов отклонений вариант от линии регрессии должна быть минимальна:

195

yдолжн, наносят эти

n

( yi y )2 min.

i 1

Это эффективный метод, позволяющий уменьшить влияние ошибок измерений.

Теперь определяют должные величины точки и соединяют их прямой линией.

Достоинство корреляционно-регрессионного анализа - наглядное представление о форме и тесноте связи. Регрессия выражает корреляционную зависимость в виде функционального отношения и дает более полную информацию.

Была исследована зависимость между ростом (X) и массой (Y), у 200 животных и рост, и масса подчиняются нормальному закону распределения. На рис. 3а видно, что эта зависимость линейная: чем больше рост, тем больше масса.

Из этой совокупности выберем выборку объема п = 10 (рис. 13.4б). Сохранилась ли эта зависимость массы от роста? На рис. 13.4б изображены 4 прямые, аппроксимирующие эту зависимость. Какую прямую можно считать наилучшей?

Рис 14.4. Зависимость между ростом (X) и массой (Y) у животных

Ответ: Да, сохранилась. Прямая I - не годится - все точки оказались по одну сторону от нее. Прямая II – слишком круто устремляется вверх.

Лучше прямые III и IV, а из них лучше та, которая ближе ко всем точкам выборки, то есть относительно которой разброс точек минимален.

196

Согласно методу наименьших квадратов лучше представляет зависимость y от х прямая IV.

По данным примера № 2:

Xi 31 32 33 34 35 35 40 41 42 46

Yi 7,8 8,3 7,6 9,1 9,6 9,8 11,8 12,1 14,7 13,0

Рассчитать параметры уравнения регрессии y ax b по формулам:

a	n( xy ) x y			;
	n( x2 ) ( x )2
b	( y )( x2 ) ( x )( xy )							.
		n( x2 ) ( x )2
					Решение:
n 10;		x 369;			y 103,8;
x2 13841;			xy 3930,1;
a	10 3930,1 369 103,8				0,44;
	10 13841 3692
b	103,8 13841 369 3930,1					6;
		10 13841 3692

y 0,44x 6.

Именно это уравнение задает прямую IV в задаче № 6.

В примере № 2 был рассчитан коэффициент корреляции между ростом (X) и массой (Y) некоторых животных, а в примере № 7 было составлено уравнение линейной регрессии.

Как вы думаете, если поменять х и у, то изменится ли уравнение регрессии и коэффициент корреляции?

Ответ: r - останется прежним, r = 0,925 - он симметричен, а уравнение регрессии получится другим. Получается, что связь роста с массой одна, а роста с массой - другая. Регрессионный анализ асимметричен - это мешает его использовать для характеристики силы связи.

197

Провести корреляционно-регрессионный анализ. Построить корреляционное поле точек, проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными X и Y и построить линию регрессии.

Изучали зависимость между содержанием вещества X в ткани С и приростом концентрации вещества Y в крови у пациентов, получавших препарат А.

Результаты наблюдений приведены в виде двумерной выборки объема 10:

xi	1,15	1,9	3	5,34	5,4	7,7	7,9	9,03	9,37	10,1
										8
yi	0,99	0,98	2,6	5,92	4,33	7,68	9,8	9,47	10,6	12,9
									4

Результаты расчета на компьютере:

r = 0,94; tнабл = 6,17; y = 0,579 + 1,1354 ∙ х

	Решение:
Н0: rген = 0;	Н1: rген ≠ 0.

Найдем из таблицы tкрит = 2,31; α ≤ 0,05; f = 10 - 2 = 8.

Сравним: tнабл > tкрит(α, f); 6,17 > 2,31.

Отвергается H0 принимается H1.

Имеется очень сильная линейная корреляционная связь между признаками r = 0,94 (α ≥ 0,05).

Построим корреляционное поле точек (рис. 13.5).

Рис. 13.5. График решения задачи 9

Рассчитаем должные величины:

при x = 0, y = -0,576;

198

при х = 1, y = 0,556.

Нанесем линию регрессии на график.

14.5. Нелинейная регрессия

Если график регрессии y = f(x) изображается кривой линией (рис. 6), то это нелинейная регрессия.

Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, литературных источников, профессионального мнения и визуального наблюдения расположения точек корреляционного поля. Этот очень важный этап анализа называется спецификацией.

Наиболее часто встречаются следующие виды уравнений нелинейной регрессии:

y a0 a1 x ... an xn - полиномиальное уравнение;

y ax2 bx c - уравнение параболы второго порядка;

y ax3 bx2 cx d - уравнение параболы третьего порядка;

y a b - гиперболическое уравнение.

x

Для определения неизвестных параметров регрессии используется метод наименьших квадратов.

По данным таблицы исследовать зависимость урожайности зерновых культур Y (кг/га) от количества осадков X (см), выпавших в вегетационный период.

n:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15;
xi:	25	27	30	35	36	38	39	41	42	45	46	47	50	52	53;
yi:	23	24	27	27	32	31	33	35	34	32	29	28	25	24	25.

Построить корреляционное поле точек и предположить наиболее подходящий вид уравнения регрессии.

Решение:

Увеличение количества выпавших осадков приведет к увеличению урожайности до некоторого предела, после чего урожайность будет снижаться. Учитывая расположение точек

199

корреляционного поля, можно предположить, что наиболее подходящим уравнением регрессии будет уравнение параболы.

Рис. 14.6. Нелинейная регрессия

14.6.Варианты заданий

►Провести корреляционно-регрессионный анализ: построить корреляционное ноле точек; проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными Х и Y;

построить линию регрессии.

№ 14.1. Изучали зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества, возраст 36-50 лет).

Результаты наблюдений приведены в виде двумерной выборки объема 5:

xi:	13,98	15,84	7,26	7,74	8,82;
yi:	35,50	42,82	47,79	43,29	49,47.

Результаты расчета на компьютере:

r = - 0,85; тr = 0,3; tнабл = 2,84; y = -1,04 х + 58,97.

№ 14.2. Изучали зависимость между содержанием коллагена Y и эластина Х в магистральных артериях головы (г/100 г сухого вещества, возраст 51-75 лет).

Результаты наблюдений приведены в виде двумерной выборки объема 5:

	xi:	13,50	13,09		6,45			7,26		8,80;
	yi:	33,97	38,07		53,98			46,00		48,61.
	Результаты	расчета на компьютере:
r = -0,94; mr = 0,2; tнабл = 4,8;						= -2,3 х + 66,8.
					y

200