Matematika_Praktikum

D(X) = (0 5,36)20,15 + (1 - 5,36)20,11 +...+ (10-5,36)20,2 =13,6. D(Y) =(0 5,36)20,01 + (1 - 5,36)20,03 +...+ (10-5,36)20,02 =4,17.

Ответ: Дисперсия меньше у второго стрелка.

12.2.4. Плотность вероятности непрерывных случайных величин

Плотностью вероятности, или плотностью распределения f(x) непрерывной случайной величины Х, называется производная её функции распределения:

f(x) = F' (x).

Ее также называют дифференциальной функцией распределения. График плотности распределения f(x) называется кривой распределения.

Рис. 12.4. Плотность распределения

Свойства плотности вероятности: 1.f(х) 0 (свойство неотрицательности).

2.Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице (свойство нормированности).

3.Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b.

Геометрическая интерпретация:

Полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [а, b]. Непрерывная случайная величина описывается следующими числовыми характеристиками:

1. Математическое ожидание: M(X) x f (x)dx

161

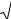
2. Дисперсия: D(X) (x M(X))2 f (x)dx или

D(X) x2 f (x)dx (M(X))2

Найдите математическое ожидание и дисперсию случайной величины X, если плотность распределения:

0,	ïðè			x 0;
	ïðè			0 x 1;
f (x) 1,
	ïðè			x 1.
0,
Решение:													1
0				1				1	x	2					1		.
M(X)	0 xdx 1 xdx 0 xdx xdx
				0		1		0	2				0	2
																					2				1
0		2		1	2		2			2				1		2			1			x3				1 1
D(X) 0 x			dx 1 x			dx 0 x		dx (M(X))					x					dx
																			2
				0		1								0								3			0	4 12

.

12.2.5. Нормальный закон распределения

Этот закон наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения. Нормальное распределение является одним из самых важных распределений в статистике. Обычно всё сравнивают с нормальным законом распределения.

Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами µ и σ2, если ее

плотность вероятности имеет вид:

		1			e	(x )2
f (x)						2 2	(см. рис. 12.5а).
			2

Свойства плотности распределения вероятностей:

Она колоколообразная ("колокол Гаусса"), иначе унимодальная. Плотность определяется двумя параметрами: математическим ожиданием (µ) и средним квадратическим отклонением (σ).

Симметричная относительно среднего.

Среднее и медиана нормального распределения равны.

162

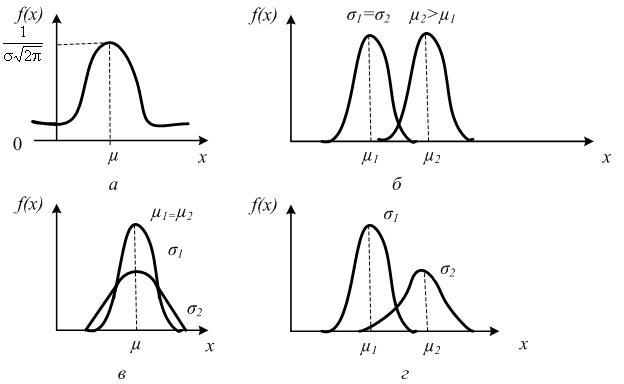
Кривая сдвигается вправо, если среднее увеличивается при постоянном квадратическом отклонении (рис. 11.56), и сдвигается влево, если среднее уменьшается.

Кривая расширяется, если среднее квадратическое отклонение σ увеличивается (если среднее постоянно).

Кривая становится более остроконечной с меньшей шириной основания колокола, σ если уменьшается при среднем постоянном (площадь под графиком всегда равна 1) (рис. 11.5в).

Рис. 12.5. Кривая нормального закона распределения и ее изменение при изменении параметров

Дополнительные свойства:

Вероятность того, что нормально распределенная случайная величина X со средним µ и средним квадратическим отклонением σ (стандартное отклонение) находится между (µ-σ) и (µ+σ), равна 0,68, т.е. 68% случайной величины X отличается от среднего не более чем на одно стандартное отклонение ± σ (рис. 11.6).

Вероятность того, что нормально распределенная случайная величина X находится между (µ-2σ) и (µ+2σ), равна 0,95, т.е. примерно 95% случайной величины X отличается от среднего на два стандартных отклонения ±2σ (рис.11.6).

Вероятность того, что нормально распределенная случайная величина X находится между (µ-3σ) и (µ+3σ), равна 0,99, т.е. 99%

163

(практически достоверно). Это свойство носит название правило трех сигм (рис. 12.6).

Рис. 12.6. Правило трех сигм

Пример 8.

Построить графики для случая µ2> µ1; σ2>σ1.

Решение. Рис. 11.5г.

12.3. Варианты заданий

№12.1. Случайная величина X задана законом распределения:

	2	3	10
	0,1	0,4	0,5

Найти математическое ожидание и среднее квадратическое отклонение. Построить многоугольник распределения.

№12.2. Найти дисперсию случайной величины X, зная закон ее распределения. Построить многоугольник распределения.

		-1			1			2	3
		0,48			0,01			0,09	0,42
№12.3. Дискретная случайная величина X имеет закон
распределения.
	0,2		0,4			0,6		0,8		1
	0,1		0,2			0,4		P4		0,1

Чему равна вероятность Р4(X=0,8)? Построить многоугольник распределения. Найти математическое ожидание и дисперсию. №12.4. Дискретная случайная величина X имеет закон

распределения.
	3	4	5	6	7
	P1	0,15	P3	0,25	0,35

164

Найти вероятность Р1(х = 3) и P3(х = 5), если известно, что Р3 в 4 раза больше Р1. Построить многоугольник распределения. Найти математическое ожидание и дисперсию.

№12.5. Дискретная случайная величина x – число мальчиков в семьях с 3 детьми. Предполагая равновероятными рождения мальчика и девочки: а) составьте ряд распределения числа рождений мальчиков; б) постройте многоугольник распределения.

№12.6. 2 стрелка стреляют по одной мишени, делая независимо друг от друга по 2 выстрела. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго – 0,6. Найдите закон распределения случайной величины x, равной общему числу попаданий в мишень.

№12.7. Дискретная случайная величина x задана таблицей распределения:

xi	-1	0	1
pi	0,25	0,5	0,25

Найдите функцию распределения F(x) и, используя ее, найдите вероятность события x 0. Постройте график функции F(x). №12.8. Случайная величина X имеет плотность вероятности

0, x 0 f(x) 3x2 ,0 x 1

0,x 1

Найдите функцию распределения F(x) и вероятность события

2 x 1 . 2

№12.9. Плотность вероятности случайной величины x, распределенной равномерно на отрезке a,b , имеет вид:

0, x a

1

f(x) ,a x bb-a

0,x b

Найдите математическое ожидание величины x.

№12.10. Даны все возможные значения дискретной случайной величины X: x1=1, x2=2, x3=3, а также известны M(X) 2,3, M X 2 5,9. Найдите закон распределения величины x.

165

№12.11. Найдите математическое ожидание и среднее квадратическое отклонение случайной величины x, имеющей плотность вероятности

		1				x 2 2
						18 .
f(x)					e
	3
			2

Пользуясь правилом «трех сигм», укажите интервал, симметричный относительно математического ожидания, в который попадает случайная величина x с вероятностью 0,9973.

Глава 13. Статистический анализ результатов исследований

13.1. Основные понятия математической статистики

Математическая статистика – это раздел математики, изучающий приближенные методы сбора и анализа данных по результатам эксперимента для выявления существующих закономерностей, т.е. отыскания законов распределения случайных величин и их числовых характеристик.

В математической статистике принято выделять два основных направления исследований:

1.Оценка параметров генеральной совокупности.

2.Проверка статистических гипотез (некоторых априорных предположений).

Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.

Генеральной совокупностью является набор всех мыслимых статистических данных при наблюдениях случайной величины.

ХГ = {х1, х2, х3, …, хN, } = { хi ; i=1,N }

Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность – есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой.

ХВ = {х1, х2, х3, …, хn, } = { хi ; i=1,n }

ХВ ХГ,

n N

166

Выборка – это совокупность случайно отобранных наблюдений (объектов) из генеральной совокупности для непосредственного изучения. Количество объектов в выборке называется объемом выборки и обозначается n. Обычно выборка составляет 5%-10% от генеральной совокупности.

Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным.

Например, популяция представляет собой множество индивидуумов. Изучение целой популяции трудоемко и дорого, поэтому собирают данные по выборке индивидуумов, которых считают представителями этой популяции, позволяющими сделать вывод относительно этой популяции.

Однако, выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Как сформировать репрезентативную (представительную) выборку? В идеале стремятся получить случайную (рандомизированную) выборку. Для этого составляют список всех индивидуумов в популяции и случайно их отбирают. Но иной раз затраты при составлении списка могут оказаться недопустимыми и тогда берут приемлемую выборку, например, одну клинику, больницу и исследуют всех пациентов в этой

клинике с данным заболеванием.
Каждый элемент выборки xi		называется вариантой. Число
повторений варианты xi	в выборке называется частотой
встречаемости ni . Величина	i		ni	называется относительной
			n

частотой варианты, т.е. находится как отношение абсолютной частоты варианты xi ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.

Рассмотрим три формы вариационного ряда: ранжированный, дискретный и интервальный.

Ранжированный ряд - это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака.

167

Дискретный вариационный ряд представляет собой таблицу, состоящую из граф, либо строк: конкретного значения признака хi и абсолютной частоты ni (или относительной частоты ωi) проявления i-го значения признака x.

Примером вариационного ряда служит таблица

Значение	xi	14	14,3	14,7	15,0	15,5
Частота	ni	0,08	0,16	0,29	0,34	0,13

Статистическое распределение – это совокупность вариант xi и соответствующих им частот ni . Для проверки правильности записи статистического распределения используют условие

n
нормировки: i		1.
i 1
Задано распределение частот выборки объема n=20.
xi		2	6		12
ni		3	10		7

Написать распределение относительных частот.

Решение: Найдем относительные частоты. Для этого разделим частоты на объем выборки:

	n1		3	0,15;	n2		10	0,5;	n3		7	0,35.
	n		20		n				n		20
						20
Распределение относительных частот имеет вид:
				xi				2					6		12
				i				0,15					0,5		0,35

Контроль: 0,15 + 0,5 + 0,35 = 1.

Дискретный ряд можно изобразить графически. В прямоугольной декартовой системе координат отмечаются точки с координатами (xi,ni ) или (xi, i ), которые соединяются прямыми линиями. Такую ломаную называют полигоном частот.

168

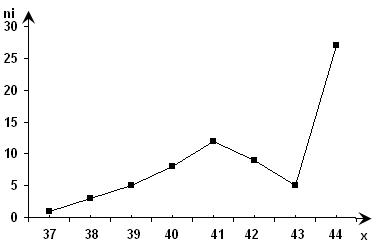
Построить дискретный вариационный ряд (ДВР) и начертить полигон распределения 45 абитуриентов по числу баллов, полученных ими на приемных экзаменах:

39 41 40 42 41 40 42 44 40 43 42 41 43 39 42 41 42 39 41 37 43 41

38 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 38 39 41 41

42.

Решение: Для построения вариационного ряда различные значения признака x (варианты) располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту.

xi	37	38	39	40	41	42	43	44
ni	1	3	5	8	12	9	5	27
Построим полигон этого распределения:

Рис. 13.1. Полигон частот

Интервальный вариационный ряд используется при большом числе наблюдений. Для построения такого ряда надо выбрать число интервалов признака и установить длину интервала. При большом числе групп величина интервала будет минимальна. Число групп в вариационном ряду можно найти по формуле Стерджеса: k 1 3,32lgn (k-число групп, n - объем выборки), а

	ширину интервала – xi		xmax xmin		R
			k		k

где xmax - максимальное; xmin - минимальное значения вариант, а их разность R носит название размаха вариации.

169

Исследуется выборка из 100 человек из совокупности всех студентов медицинского ВУЗа.

Решение: Рассчитаем число групп: k 1 3,32lg100 7,64. Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.

Для наглядного представления статистического распределения пользуются гистограммой.

Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высота равна или частоте попадания в интервал ni или относительной частоте ωi.

Наблюдения за числом частиц, попавших в счетчик Гейгера, в течение минуты дали следующие результаты:

21 30 39 31 42 34 36 30 28 30 33 24 31 40 31 33 31 27 31 45 31 34

27 30 48 30 28 30 33 46 43 30 33 28 31 27 31 36 51 34 31 36 34 37

28 30 39 31 42 37.

Построить по этим данным интервальный вариационный ряд с равными интервалами (I интервал 20-24; II интервал 24-28 и т.д.) и начертить гистограмму.

Решение: n=50

Интервал	20-	24-	28-	32-	36-	40-	44-	48-
	24	28	32	36	40	44	48	52
Частота ni	1	4	22	8	7	4	2	2

Гистограмма этого распределения имеет вид:

170