Matematika_Praktikum

10.Имеется 1000 относительных единиц радона. Сколько

действующих единиц радона останется СПУСТЯ 1 ч? Постоянная распада радона λ=2,1·10-6с-1

11.Определять, какая доля ядер 80Bi210 распадается за 1 ч, если постоянная распада 80Bi210 λ= 1,61·10-6с-1

10.9.Контрольные вопросы

1.Дайте определение дифференциального уравнения. Математическая запись ДУ. Примеры представления ДУ.

2.Что такое порядок ДУ? Приведите примеры записи ДУ различных порядков.

3.Дайте определение решения (интеграла) ДУ, общего решения, частного решения, начальных условий.

4.В чем состоит задача Коши?

5.В чем заключается интегрирование ДУ?

6.Что такое интегральная кривая? Чем отличаются графически общее решение ДУ и частное решение ДУ?

7.Дайте определение и приведите примеры ДУ с разделяющимися переменными.

8.Что такое однородная функция степени n?

9.Дайте определение и приведите примеры однородного ДУ.

10.Дайте определение линейного ДУ 1-го порядка.

11.Перечислите и объясните суть методов решений ЛНДУ 1-го порядка.

12.Приведите примеры применения дифференциальных уравнений в биологии и медицине.

Глава 11. Численные методы решения дифференциальных уравнений

Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса уравнений. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.

111

В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.

Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.

Рассмотрим некоторые из них.

11.1. Метод Эйлера

Известно, что уравнение y f (x, y) задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.

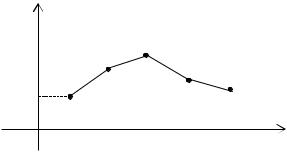
Если взять последовательность точек х0, х1, х2, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию (рис. 11.1).

При подстановке заданных начальных условий (х0, у0) в дифференциальное уравнение y f (x, y)получаем угловой коэффициент касательной к интегральной кривой в начальной точке

tg 0 y f (x0, y0).

Заменив на отрезке [x0, x1] интегральную кривую на касательную к ней, получаем значение

y1 y0 f (x0, y0)(x1 x0).

Производя аналогичную операцию для отрезка [x1, x2], получаем:

	y			y2 y1 f (x1, y1)(x2 x1).
				Продолжая подобные действия
	M1	M2	M3	далее, получаем ломаную кривую,
				которая	называется	ломаной
y0	M0		M4	Эйлера.
				Можно	записать	общую
0	x0 x1	x2	x3 x4 x	формулу вычислений:
	Рис. 11.1.

112

y0 f (x0, y0)

y1 y0 f (x0, y0)h

yn yn 1 f (xn 1, yn 1)(xn xn 1).

Если последовательность точек хi выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:

yn yn 1 f (xn 1, yn 1)h

Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.

Суть метода состоит в том, что в формуле вместо значения берется среднее арифметическое значений f(x0, y0) и f(x1, y1). Тогда уточненное значение:

y1(1) y0 f (x0, y0)2 f (x1, y1) h

Затем находится значение производной в точке (x1, y1(1)). Заменяя f(x0, y0) средним арифметическим значений f(x0, y0) и f (x1, y1(1)), находят второе уточненное значение у1:

y1(2) y0 f (x0, y0) 2 f (x1, y1(1)) h,

Затем третье:

y1(3) y0 f (x0, y0) 2f (x1, y1(2)) h,

и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М1 ломаной Эйлера.

Аналогичная операция производится для остальных значений

у.

Подобное уточнение позволяет существенно повысить точность результата.

10.2. Метод Рунге – Кутта

Метод Рунге – Кутта является более точным по сравнению с методом Эйлера.

113

Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора.

		yi yih yi	h2	yi	h3	IV	h4
	yi 1					yi		...
			2!		3!		4!

Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.

yi 1	yi yih yi	h2	yi	h3	yi yi.
	2!		3!

В методе Рунге – Кутта приращения yi предлагается вычислять по формуле:

yi	1	k(i)	2k	(i)	2k	(i)	k	(i)
				2		3
6		1						4

где коэффициенты ki вычисляются по формулам:

		k1(i) hf (xi , yi )
					h				(i)
k	(i)	hf x	i			; y	i		k1
	2
				2				2
					h				(i)
k	(i)	hf x	i			; y	i		k2
	3
				2				2

k4(i) hf xi h; yi k3(i)

10.3. Примеры

№1. Решить методом Рунге – Кутта дифференциальное уравнение y x y при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.

Решение.

Для i = 0 вычислим коэффициенты ki:

k1(0) hf (x0, y0) 0,1(x0 y0) 0,1(0 1) 0,1;

					h				k	(0)		0,1 0,05 1,05 0,11;
k	(0)	hf x	0			; y	0		1
					2
	2									2

114

					h				k	(0)
k	(0)	hf x	0			; y	0			2		0,1(0,05 1,055) 0,1105;
					2					2
	3

k4(0) hf x0 h; y0 k3(0) 0,1(0,1 1,1105) 0,1211;

1		(0)	(0)	(0)	(0)		1
y0		(k1	2k2	2k3	k4	)		(0,1 0,22 0,221 0,1211) 0,1104;
	6						6
x1 x0 h 0,1;
y1 y0		y0	1 0,1104 1,1104;

Последующие вычисления приводить не будем, а результаты представим в виде таблицы.

i	xi		k			yi	yi
		1			0,1000
0	0	2			0,1100	0,1104	1
		3			0,1105
		4			0,1211
		1			0,1210
1	0,1	2			0,1321	0,1325	1,1104
		3			0,1326
		4			0,1443
		1			0,1443
2	0,2	2			0,1565	0,1569	1,2429
		3			0,1571
		4			0,1700
		1			0,1700
3	0,3	2			0,1835	0,1840	1,3998
		3			0,1842
		4			0,1984
		1			0,1984
4	0,4	2			0,2133	0,2138	1,5838
		3			0,2140
		4			0,2298
5	0,5						1,7976
					115

№2. Решим предыдущий пример методом Эйлера.

Решение.

Применяем формулу yn yn 1 hf (xn 1, yn 1)

x0 0,	y0 1,		f (x0 , y0 ) x0 y0 1
hf (x0, y0) h(x0 y0) 0,1
y1 y0	hf (x0, y0) 1 0,1 1,1
x1 0,1	y1 1,1		f (x1, y1) x1 y1 1,2

hf (x1, y1) h(x1 y1) 0,12

y2 y1 hf (x1, y1) 1,1 0,12 1,22

Производя аналогичные вычисления далее, получаем таблицу значений:

i	0	1	2	3	4	5
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi	1	1,1	1,22	1,362	1,528	1,721

Применим теперь уточненный метод Эйлера (точность 0,001).

i	0	1	2	3	4	5
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi	1	1,111	1,243	1,400	1,585	1,799

Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.

Уравнение y y x является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.

y y 0;

y y;

dy

y;

dy

dx;

dy

dx;

dx

y

y

y

x lnC;

y

x;

y Cex;

ln

ln

C

Решение неоднородного уравнения имеет вид y C(x)ex .

y C (x)ex C(x)ex;

x

C(x)e

x

x C(x)e

x

;

C

x

x;

x

;

C (x)e

(x)e

C (x) xe

116

			dv e	x
С(x)		u x;			dx;		xe	x		e xdx
		xe xdx		x
			v e		;
		du dx;
xe x e x C;
Общее решение: y Cex x 1.
C учетом начального условия: 1 C 0 1;								C 2.
Частное решение: y 2ex x 1.

Для сравнения полученных результатов составим таблицу.

			yi
i	xi	Метод	Уточнен-		Метод	Точное
		Эйлера	ный метод		Рунге-	значение
			Эйлера		Кутта
0	0	1	1		1	1
1	0,1	1,1	1,111		1,1104	1,1103
2	0,2	1,22	1,243		1,2429	1,2428
3	0,3	1,362	1,4		1,3998	1,3997
4	0,4	1,528	1,585		1,5838	1,5837
5	0,5	1,721	1,799		1,7976	1,7975

Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем что, во-первых, полученное приближенное значение округляется на каждом шаге, а во-вторых – тем что, в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом, происходит накопление ошибки.

Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.

11.4. Варианты заданий

117

№11.1. Решить с помощью методов Эйлера, уточненного метода Эйлера, Рунге-Кутта и аналитически следующие дифференциальные уравнения при заданных начальных условиях, на заданном отрезке с шагом 0,2. Сравнить полученные результаты.

№

Уравнение

Начальные условия

Отрезок

варианта

y f (x, y)

(x0, y0)

[x0, xк]

1

y x 1

x0= –1, y0= 0

[–1, 1]

2

y y x

x0= 0, y0= 2

[0, 2]

3

y (y 1)2

x0= 1, y0= 0

[1, 3]

4

y x(y 1)

x0= 0, y0= 2

[0, 2]

5

y 1 2x

x0= 0, y0= 2

[0, 2]

6

y

x 1

x0= 1, y0= 1

[1, 3]

y

7

y

y

x0= 1, y0= 1

[1, 3]

x

8

y

2y

x0= 1,y0= 2

[1, 3]

x

9

y x2 y

x0= 0, y0= 2

[0, 2]

10

y 2x 3

x0= 2, y0= 0

[2, 4]

11

y y 2x

x0= 0, y0= 3

[0, 2]

12

y (y 1)2

x0= –3, y0= –2

[–3, –1]

13

y 2(x 2)y

x0= –2, y0= 1

[–2, 0]

14

y 1 4x

x0= –3, y0= 5

[–3, –1]

15

Y

X

X0= - 4,Y0= 4

[-4,-2]

Y 1

16

Y

1 Y

X0= 2,Y0= 2

[2,- 4]

X 2

17

Y

3(Y 1)

X0= 3,Y0= 0

[3,5]

X 2

2Y 6X

X0= 0,Y0= -2

[0,2]

18

Y

118

19

Y

1 Y2

X0= -3,Y0= 1

[-3,-1]

XY

20

Y 2

X0= 2,Y0= 9

[2,4]

Y

21

Y

X(1 2

X0= -2,Y0= -0.4

[-2,0]

1 X2

22

Y

Y

X0= - 4,Y0= -2

[-4,-2]

1 X

23

Y

Y

X0= 0,Y0= 2

[0,2]

2 1 X

24

Y

Y2

X0= 1,Y0= 1

[1,3]

X

2

11.4. Контрольные вопросы

1.Когда применяются численные методы решения дифференциальных уравнений?

2.Перечислите известные вам численные методы решения дифференциальных уравнений.

3.В чем заключается суть метода Эйлера?

4.В чем смысл уточненного метода Эйлера?

5.В чем смысл метода Рунге-Кутта?

6.Как рассчитать погрешность вычислений в приближенных методах?

Глава 12. Элементы теории вероятностей

12.1. Случайное событие

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.

Теория вероятности изучает случайные события и случайные величины.

119

Случайное событие – это любой факт, который в результате испытания может произойти или не произойти. Случайное событие – это результат испытания.

Испытание (опыт, эксперимент) – в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может проводиться человеком, но может осуществляться и независимо от человека. Человек в этом случае выступает в роли наблюдателя.

Событие обозначаются начальными прописными (заглавными) буквами латинского алфавита A, В, С.

1.Достоверное событие – это событие, которое в результате испытания обязательно должно произойти.

2.Невозможное событие – это событие, которое в результате испытания вообще не может произойти.

События называются несовместными, если наступление одного из них исключает появление другого. В противном случае события – совместные.

Противоположные события: два события A и A называются противоположными, если непоявление одного из них в результате данного испытания влечет появление другого. ( A читается "не А").

12.2. Комбинаторика

Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.

Размещениями из n различных элементов по m элементов (m ≤ n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком следования элементов.

Например, из трех элементов a, b, c можно составить по два элемента следующие размещения: ab, ас, bc, ba, ca, cb.

120