Matematika_Praktikum

.

	8. Область значения E(y)=R.
	3.7. Варианты заданий
№3.1. Найти интервалы монотонности следующих функций:
1.	y x2			4x 1;						4.	f (x)	sin x					на			0,				;
2.	f (x) x3 3x2 ;												x								2
						3				5.	y x(1				).
3.	f (x) x3							x2 6x;						x
					2
№3.7.2. Исследовать на экстремум следующие функции:
1.	y x2 2;									3.	f (x) x3 3x2 9x 6;
2.	y	1	x	3	2x		2		3x 1;	4.	y (x 5)ex ;
		3								5.	y 1 5							.
													(x 2)4

№3.3. Исследовать на выпуклость и вогнутость следующие функции:

1.	y 4x x2 ;											3.	y x5 ;
2.	1				3		5			2	6x;	4.	y x6 ;
	y			x					x
							2					5.	y x4 8x2 .
	3

№3.4. Найти наибольшее и наименьшее значения функции:

1.y x3 6x на отрезке [ 3, 4];

2.f (x) 2x3 6x 5 на отрезке [ 5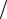2, 32];

3.f (x) 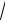100 x2 на отрезке [ 6, 8].

№3.5. Исследовать функции и построить их графики: 1. y=3x5–5x3+2;

	2.	y=	x		;
			x2 1
	3.	y=	x2	;
			x 2

31

4.	y=			1						1;
									2
		x 2
5.	y				4x2								4x 2
								x	2		1
6.	y
						x 1									x
7.	y							3
				2x										2 x
8.	y 3						3
						x							x 1

9. y 3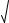(x 1)2 3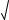x2 1

	10.	y cos xcos2x
	11.	y	cos2x
			cos x

12.y sin x cos2x

13.у = tg(x) – sin(x)

14.y = ctg(x) + cos(x)

3.8.Контрольные вопросы

1.Назовите основные пункты исследования графика функции.

2.Что называется областью определения функции?

3.Что называется областью значения функции?

4.Что является промежутками возрастания функции?

5.Что является промежутками убывания функции

6.Когда график функции имеетвыпуклость?

7.Когда график функции имеет вогнутость?

8.Чтоназывается асимптотами?

9.Какиебываютасимптоты?

10.Как найти асимптоты?

Глава 4. Функции нескольких переменных

4.1. Определение функции нескольких переменных

При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных,

32

т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

Обозначение z = f(x, y)

Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то –

многозначной.

Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию

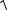
x x0 2 y y0 2 r .

Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие MM0 r , или условие f (x, y) A .

Записывают: lim f (x, y) A

x x0 y y0

4.2. Частные производные

Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х к

переменной х. Тогда величина xz = f(x + x, y) – f(x, y)

называется частным приращением функции по х.

Можно записать x z f (x x, y) f (x, y) .

x x

Тогда lim x z называется частной производной функции z =

x 0 x

f(x, y) по х. Обозначение:	z	;	zx ;	f (x, y)	;	fx (x, y).
	x			x

33

Аналогично определяется частная производная функции по у

z lim f (x, y y) f (x, y) .

y

y 0

y

4.3. Полный дифференциал

Для функции f(x, y) выражение z = f(x + x, y + y) – f(x, y)

называется полным приращением.

Выражение z	f (x, y)	x	f (x, y)	y 1 x	2 y называется
	x		y

полным приращением функции f(x, y) в некоторой точке (х, у), где 1 и 2 – бесконечно малые функции при х 0 и у 0 соответственно.

Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у часть приращения функции z в точке (х, у).

dz fx (x, y)dx fy (x, y)dy

Для функции произвольного числа переменных:

df (x, y,z,...,t)	f	dx	f	dy ...	f	dt
	x		y
					t

4.5. Примеры

№1. Найти частные производные функций:

а)

z

x

y

1

; в)

z cos

x2

y2

.

3

3

2

x3

y

x

6x

y

y3

б)

z

x2 2xy

;

y

2

2xy 1

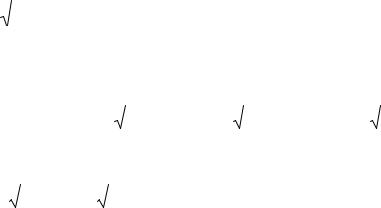
Решение.

а) Частные производные функции двух и более переменных определяются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаются постоянными.

34

																			1										n
Имеем: (напомним, что																																):
																												xn 1
																		xn
			1				1							1 1								1							3y						1
																																						;
z				(x) y
			y3											6y															x4					3x3 y
	x						x3								x2							y3
				1			1							1				1					3x								1				1
zy										(y)																														.
		x
					3			3																		4						3				2			2
				y			x							6x	2									y						x					6x			y
																		y

б) Воспользуемся правилом дифференцирования дроби:

zx			(2x 2y)(y2 2xy 1) (x2 2xy)2y		;
				(y2 2xy 1)2
zy			2x(y2	2xy 1) (x2 2xy)(2y 2x)		.
				(y2 2xy 1)2

в) Здесь имеем дело с производными сложной функции и дроби.

			2		2			2		2	/			2		2			3	3			2 2		2
z		x		y					y				x		y			2x(x		y ) 3x (x					y )
	sin						x					sin														.
			3		3			3		3						3					3	3		2
x		x		y					y				x	3	y					(x			)
						x					x											y

	Ввиду симметрии выражения	x2	y2
		x3	y3

относительно х и у

можно записать сразу

z	sin	x2 y2		2y(x3 y3 ) 3y2 (x2	y2 )	.
y		x3 y3		(x3 y3)2

№2. Найти полный дифференциал функций:

а)

u

x

;

б)

u xy2z .

y2 z2

Решение.

ux

1

,uy

xy

,uz

xz

а)

Так

как

, то

y2 z2

(y2 z2 )3

(y2 z2 )3

полный

дифференциал

имеет

вид

du

dx

xydy xzdz

.

y2 z2

(y2 z2 )3

35

б) Вычислим частные производные по х, у, z

u y2 z xy2z 1;

x

u xy2z ln x 2yz;

y

u xy2z ln xy2.

z

Таким образом, полный дифференциал

du y2zxy2z 1dx 2xy2z yzln xdy y2 xy2z ln xdz

4.6. Варианты заданий

№4.1. Найти частные производные, частные дифференциалы данных функций по каждой из независимых переменных (x, y, z, t, …) и полный дифференциал:

а) z ex2 y2

;

б)

u t5

sin3 z;

в)

z 5x2 y y3 7 3 ;

г)

z x

y

;

y

3

x

д)

z lntg

x

;

y

u x

y

е)

z

;

ж) u xy (xy)z zxy ;

з)	z x2		cos2xy y2 sin(x y)
;
и)	v x4		cos2		y y4 sin3 x5 ;
							.
к)	z ln			x2	y2
				x2	y2

4.7. Контрольные вопросы

Глава 5. Численное дифференцирование

При анализе медицинских, инженерных и научных данных часто возникает необходимость найти наклон кривой, которая задана таблицей значений.

Возможна и другая ситуация: f(x) известна, но имеет очень сложное аналитическое выражение.

36

В первом случае классические методы дифференциального исчисления просто неприемлемы, а во втором случае их использование вызывает значительные трудности. В таких задачах вместо функции f(x) рассматривают интерполирующую функцию P(x), а затем полагают f'(x) P'(x) на интервале a x b. Аналогично поступают при нахождении производных высших порядков функции f(x).

Если для интерполирующей функции P(x) известна погрешность интерполяции R(x)=f(x)–P(x), то погрешность производной равна производной от погрешности этой функции

r(x)=f '(x)–P'(x)=R'(x).

Такое утверждение справедливо и для производных высших порядков.

В целом же численное дифференцирование представляет собой операцию менее точную, чем интерполирование.

5.1. Формулы для вычисления первой производной

Численное дифференцирование весьма чувствительно к погрешностям, вызванным неточностью исходных данных. Значительно меньшую погрешность имеет дифференцирование многочленов наилучшего среднеквадратического приближения (методом наименьших квадратов). На практике часто применяются формулы безразностного дифференцирования для производной первого порядка:

По трем точкам:

1

y'0 2h( 3y0 4y1 y2)

		y'				1				( y				0		y		2	)				(5.1)
	1						2h
		y'					1				(y					4y					3y		)
				i			2h						i 2						i 1			i
По четырем точкам:
y'		1		( 11y					0			18y					9y					2y )
0		6h														1				2			3
y'	1		( 2y					0	3y						6y				2	y );			(5.2)
1	6h												1									3

37

1

y'2 6h(y0 6y1 3y2 2y3);

y'i		1	( 2yi 3 9yi 2 18yi 1 11yi ) .
		6h

По пяти точкам:

y'0

1

( 25y0 48y1 36y2 16y3 3y4 ) ;

12h

y'1

1

( 3y0 10y1 18y2 6y3 y4 ) ;

12h

y'2

1

(y0 8y1 8y3 y4 ) ;

(5.3)

12h

y'3

1

( y0 6y1 18y2 10y3 3y4 );

12h

y'i

1

(3yi 4 16yi 3 36yi 2 48yi 1 25yi ).

12h

5.2. Формулы второй производной

По четырем точкам:

yi//

1

(2y0 5y1 4y2 y3); (первое значение)

h2

yi//

1

(yi 1 2yi yi 1);

(внутренние точки)

(5.4)

h2

yi//

1

( yi 3 4yi 2 5yi 1 2yi ). (последнее значение)

h2

По пяти точкам:

y0//

1

(35yi 104yi 1 114yi 2 56yi 3 11yi 4 );

12h2

y1//

1

(11yi 1 20yi 6yi 1 4yi 2 yi 3 );

12h2

y2//

1

( yi 2 16yi 1 30yi

16yi 1 yi 2 );

(5.5)

12h2

y3//

1

( yi 3 4yi 2 6yi 1 20yi 11yi 4 );

12h2

yi//

1

(11yi 4 56yi 3 114yi 2 104yi 1 35yi ).

12h2

38

Заметим, что с ростом порядка производной резко падает точность численного дифференцирования. Поэтому на практике редко применяют формулы для производных второго порядка.

5.3. Примеры

№1. Пользуясь безразностными формулами по 3 точкам, определить первые производные для функции у=х2 на интервале [1; 3] с шагом 0,2 и сравнить их значения с аналитическими.

Решение.

Воспользуемся формулами (5.1):

y/					1				( 3 4 1,44 1,96)				0,8						2
					2 0,2
0												0,4
y/					1				( 1 1,96)		0,96	2,4
					2 0,2
1						0,4
y/					1				(1 4 1,44 3 1,96)					1,12									2,8
					2 0,2
2												0,4
y/					1				(1,44 4 1,96 3 2,56)											1,28									3,2
					2 0,2
3												0,4
y/					1				(1,96 4 2,56 3 3,24)												1,44								3,6
					2 0,2
4																						0,4
y/					1				(2,56 4 3,24 3 4)						1,6										4
					2 0,2
5												0,4
y/					1				(3,24 4 4 3 4,84)							1,76											4,4
					2 0,2
6												0,4
y/					1				(4 4 4,84 3 5,76)								1,92										4,8
					2 0,2
7												0,4
y/					1				(4,84 4 5,76 3 6,76)													2,08									5,2
					2 0,2																	0,4
8
y/					1				(5,76 4 6,76 3 7,84)														2,24								5,6
					2 0,2
9																						0,4
y/					1					(6,76 4 7,84 3 9)								2,4									6
10					2 0,2							0,4

Для сравнения этих значений с аналитическими составим таблицу:

39

		у=х2	Аналитические	Численные значения
i	хi		значения
			у΄=2х	у΄
0	1	1	2	2,0
1	1,2	1,44	2,4	2,4
2	1,4	1,96	2,8	2,8
3	1,6	2,56	3,2	3,2
4	1,8	3,24	3,6	3,6
5	2	4	4	4
6	2,2	4,84	4,4	4,4
7	2,4	5,76	4,8	4,8
8	2,6	6,76	5,2	5,2
9	2,8	7,84	5,6	5,6
10	3	9	6	6

Таким образом, мы видим, что все значения первой производной полностью совпадают с аналитическими.

№2. Пользуясь безразностными формулами по 4 точкам, определить первые производные для функции у=х3 на отрезке [1; 3] с шагом 0,2 и сравнить эти значения с аналитическими.

Решение.

Пользуемся формулами (5.2):

у	/				1		( 11 1 18 1,728 9 2,744 2 4,096)							3,6		3
	0				6 0,2
									1,2
у	/				1		( 2	1	3 1,728 6 2,744 4,096)		5,184				4,32
					6 0,2
1									1,2
у	/				1		(1 6 1,728 3 2,744 2 4,096)			7,056			5,88
	2				6 0,2
									1,2
у3/					1		( 2	1	9 1,728 18 2,744 11 4,096)				9,216				7,68 и т.д.
					6 0,2
									1,2

по формуле для yi/ .

Для сравнения полученных значений с аналитическими составим таблицу:

40