
- •Модуль 2. Молекулярная физика Лекция 1
- •2.1. Статистический и термодинамический методы описания свойств
- •Макроскопических систем
- •2.2. Функции распределения
- •2.2.1. Общий подход
- •2.2.2. Функция распределения молекул идеального газа по модулю скорости молекул
- •2.2.3. График функции распределения молекул идеального газа по модулю скорости для двух температур
- •2.2.4. Функция распределения молекул идеального газа по кинетическим энергиям поступательного движения молекул
- •2.2.5. Средние характеристики молекул
- •Лекция 2
- •2.3. Основное уравнение мкт идеального газа для давления
- •2.4. Молекулярно-кинетический смысл температуры
- •2.5. Распределение Больцмана
- •2.5.1. Функция распределения Больцмана
- •2.5.2. Барометрическая формула
- •*2.7. Экспериментальная проверка распределения молекул по модулю скорости. Опыт Ламмерта
- •*2.8. Опыты Перрена по определению постоянной Авогадро
- •2.9. Основные понятия равновесной термодинамики
- •Лекция 3
- •2.10. Внутренняя энергия системы, работа, теплообмен
- •2.10.1. Внутренняя энергия системы
- •2.10.2. Работа
- •2.10.3. Теплообмен, теплоемкость системы
- •2.11. Первый закон (начало) термодинамики
- •2.12. Второе начало (закон) термодинамики. Термодинамические формулировки
- •2.13. Энтропия в термодинамике
- •Лекция 4
- •2.14. Качественный пример изменения энтропии при неравновесном процессе
- •2.15. Коэффициент полезного действия (кпд) идеального теплового двигателя
- •2.16. Число степеней свободы молекулы. Закон о равномерном распределении энергии по степеням свободы. Теплоемкость идеального газа
- •2. Молекула, состоящая из двух атомов
- •2.17. Применение первого и второго закона термодинамики к изопроцессам в идеальном газе
- •Лекция 5 *2.18. Примеры расчета изменения энтропии для неравновесных процессов.
- •2.19. Термодинамическая вероятность. Статистический смысл понятия энтропии.
- •2.20. Оценка термодинамической вероятности неравновесного и равновесного состояний.
- •Лекция 6
- •2.23. Основы физической кинетики
- •2.23.1. Уравнения для явлений переноса. Линейная неравновесная термодинамика
- •2.23.2. Формулы для коэффициентов переноса в случае идеального газа
- •2. Формулы для коэффициентов переноса
- •2.23.3. Зависимость коэффициентов переноса от параметров состояния идеального газа при протекании различных изопроцессов в идеальном газе
- •Лекция 7
- •2.24. Реальные газы. Уравнение Ван – дер - Ваальса
- •2.25. Экспериментальные и теоретические изотермы для реальных газов. Критическая точка
- •2.26. Внутренняя энергия реального газа
- •2.27. Жидкое состояние. Строение жидкости
2.2. Функции распределения
2.2.1. Общий подход
Возьмем
случайную величину Х, которая принимает
конечный дискретный набор значений
![]() (
(![]() ).
Тогда вероятностью
).
Тогда вероятностью![]() выпадения в отдельном опыте какого-либо
значения
выпадения в отдельном опыте какого-либо
значения![]() этой величины называется предел отношения
числа опытов
этой величины называется предел отношения
числа опытов![]() ,
при которых выпадает это значение
,
при которых выпадает это значение![]() ,
к общему числу опытов
,
к общему числу опытов![]() ,
при стремлении общего числа опытов к
бесконечности
,
при стремлении общего числа опытов к
бесконечности
![]() =
=![]() .
(2.1)
.
(2.1)
При
конечном числе опытов отношение (![]() )
будет отличаться в ту или иную сторону
от значения
)
будет отличаться в ту или иную сторону
от значения![]() ,
и при возрастании общего числа
,
и при возрастании общего числа![]() опытов эти отклонения будут становиться
все меньше и меньше, приближаясь к
опытов эти отклонения будут становиться
все меньше и меньше, приближаясь к![]() .
.
Так,
например, вероятность выпадения “орла”
при бросании монеты равна
![]() .
Это означает, что при бросании монеты
в 50% опытов при стремлении их общего
числа к бесконечности будет выпадать
“орел”. При конечном числе опытов
величина
.
Это означает, что при бросании монеты
в 50% опытов при стремлении их общего
числа к бесконечности будет выпадать
“орел”. При конечном числе опытов
величина![]() будет отличаться от значения 0,5 и тем
существеннее, чем меньше общее число
опытов
будет отличаться от значения 0,5 и тем
существеннее, чем меньше общее число
опытов![]() .
.
Рассмотрим
теперь непрерывно распределенную
случайную величину Х,
которая принимает непрерывный набор
действительных чисел в диапазоне от
нуля до бесконечности. В этом случае
вероятность выпадения конкретного
значения случайной величины будет равна
нулю, так как число опытов (набор
натуральных чисел) не перекрывает всего
набора действительных чисел. Так,
например, вероятность выпадения значения
х =
200,00546 будет равна нулю
![]() .
.
В
связи с этим рассматриваются вероятности
попадания случайной величины в отдельном
опыте в определенный интервал значений.
Для этого вводится функция распределения
![]() ,она представляет
собой плотность вероятности или отношение
вероятности
,она представляет
собой плотность вероятности или отношение
вероятности
![]() попадания значения случайной величины
в отдельном опыте в бесконечно малый
интервал значений (
попадания значения случайной величины
в отдельном опыте в бесконечно малый
интервал значений (![]() )
к величине этого интервала
)
к величине этого интервала
![]()
![]() .
(2.2)
.
(2.2)
С
помощью этой функции можно получить
вероятность
![]() попадания значения случайной величины
Х в любой интервал значений (
попадания значения случайной величины
Х в любой интервал значений (![]() ,
,![]() )
)
![]() =
=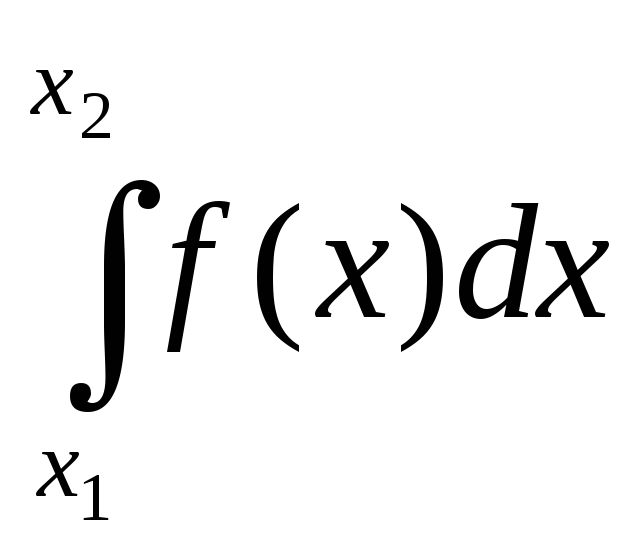 .
(2.3,а)
.
(2.3,а)
Для
малого интервала значений (![]() ),
в пределах которого с достаточной
степенью точности в условиях данной
конкретной задачи можно считать, что
функция распределения
),
в пределах которого с достаточной
степенью точности в условиях данной
конкретной задачи можно считать, что
функция распределения![]() не изменяется по величине, формула
(2.3,а) запишется таким образом
не изменяется по величине, формула
(2.3,а) запишется таким образом
![]() .
(2.3,б)
.
(2.3,б)
Если
взять интервал значений равным области
существования случайной величины
(например, в пределах от нуля до
бесконечности), то тогда вероятность
выпадения какого-то значения случайной
величины будет равна единице (![]() ),
так как это будет достоверным событием
),
так как это будет достоверным событием
![]() .
(2.4)
.
(2.4)
Выражение (2.4) получило название условия нормировки.
С
помощью функции распределения
![]() можно рассчитать величины, которые
характеризуют всю совокупность значений
случайной величиных,
такие, например, как среднее арифметическое
значение
можно рассчитать величины, которые
характеризуют всю совокупность значений
случайной величиных,
такие, например, как среднее арифметическое
значение
![]() ,
среднее квадратичное значение
,
среднее квадратичное значение![]()
![]() ,
,
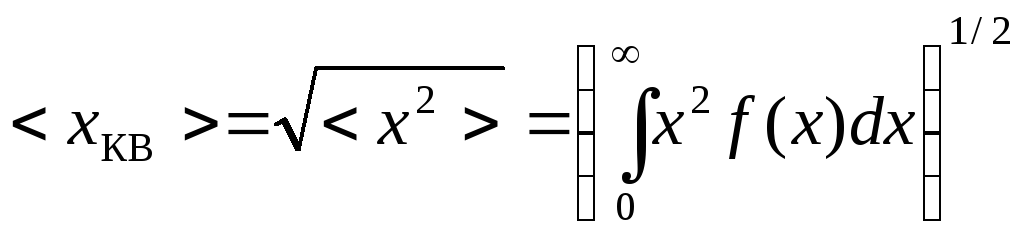 .
(2.5)
.
(2.5)
Рассмотрим конкретные примеры функций распределения.
