Матан, Лекции - Теляковский 1

x 5.2. dIFFERENCIAL FUNKCII

oPREDELENIE. pUSTX FUNKCIQ y = f(x) OPREDELENA W NEKOTOROJ OKRESTNOSTI TO^KI x. eSLI PRIRA]ENIE FUNKCII f W \TOJ TO^KE MOVET BYTX PREDSTAWLENO W WIDE

y = A x + o( x) x ! 0

(5.2.1)

GDE A | NEKOTOROE ^ISLO, TO GOWORQT, ^TO FUNKCIQ f DIFFERENCIRUEMA W TO^KE x.

iNOGDA NUVNO RASSMATRIWATX PRIRA]ENIE y I PRI x = 0. w \TOM SLU^AE S^ITA@T, ^TO PRI x = 0 OSTATO^NYJ ^LEN W FORMULE (5.2.1) RAWEN NUL@.

tEOREMA 5.2.1. dLQ TOGO ^TOBY FUNKCIQ y = f(x) BYLA DIFFERENCIRUEMA W TO^KE x0, NEOBHODIMO I DOSTATO^NO, ^TOBY f IMELA W \TOJ TO^KE PROIZWODNU@. eSLI \TO USLOWIE WYPOLNENO, TO

y = f0(x0) x + o( x) x ! 0:

(5.2.2)

dOKAZATELXSTWO. pRI DOKAZATELXSTWE TEOREMY 5.1.1 MY WIDELI, ^TO IZ SU]ESTWOWANIQ PROIZWODNOJ FUNKCII f W TO^KE x SLEDUET OCENKA (5.1.2), KOTORU@ W SILU (5.1.3) MOVNO ZAPISATX KAK (5.2.2). oTS@DA SLEDUET DOSTATO^NOSTX W TEOREME 5.2.1.

~TOBY DOKAZATX NEOBHODIMOSTX, RAZDELIM OBE ^ASTI (5.2.1)

NA x:	y
		= A + o(1) x ! 0:
	x

|TO SOOTNO[ENIE OZNA^AET, ^TO FUNKCIQ f IMEET W TO^KE x PROIZ- WODNU@, RAWNU@ A, T.E. IZ (5.2.1) SLEDUET (5.2.2).

tEOREMA DOKAZANA.

tAKIM OBRAZOM, RAWNOSILXNY UTWERVDENIQ, ^TO FUNKCIQ IMEET W NEKOTOROJ TO^KE PROIZWODNU@ I ^TO FUNKCIQ DIFFERENCIRUEMA W \TOJ TO^KE.

eSLI DLQ PRIRA]ENIQ FUNKCII f IMEET MESTO PREDSTAWLENIE (5.2.1), TO SLAGAEMOE A x NAZYWA@T LINEJNOJ ^ASTX@ PRIRA]ENIQ FUNKCII f.

oPREDELENIE. eSLI FUNKCIQ f(x) DIFFERENCIRUEMA W TO^KE, TO LINEJNU@ ^ASTX PRIRA]ENIQ FUNKCII NAZYWA@T DIFFERENCIALOM FUNKCII W \TOJ TO^KE I OBOZNA^A@T df ILI df(x).

tAKIM OBRAZOM,

df(x) := f0(x) x:

(5.2.3)

91

pOD^ERKNEM, ^TO ZDESX RE^X IDET O DIFFERENCIALE FUNKCII f KAK FUNKCII ARGUMENTA x.

w OB]EM SLU^AE dy 6= y, TAK KAK W SILU (5.2.2) PRIRA]ENIE y IMEET E]E SLAGAEMOE o( x).

dLQ EDINOOBRAZIQ OBOZNA^ENIJ NARQDU S DIFFERENCIALOM FUNK- CII WWODQT DIFFERENCIAL NEZAWISIMOJ PEREMENNOJ, POLAGAQ PO OPREDELENI@ dx := x.

eSLI ISPOLXZOWATX DIFFERENCIAL NEZAWISIMOJ PEREMENNOJ, TO DIFFERENCIAL FUNKCII dy MOVNO ZAPISATX TAK: dy = f0(x) dx, OT- KUDA

f0(x) =	dy	:	(5.2.4)
	dx

sLEDOWATELXNO, PROIZWODNAQ RAWNA OTNO[ENI@ DIFFERENCIALA FUNKCII K DIFFERENCIALU NEZAWISIMOJ PEREMENNOJ. iNOGDA RAWEN- STWO (5.2.4) RASSMATRIWA@T PROSTO KAK DRUGOE OBOZNA^ENIE PROIZ- WODNOJ.

dLQ DIFFERENCIALOW SPRAWEDLIWY SLEDU@]IE FORMULY:

d(u		v) = du dv
d(u v) = u dv + v du
I, ESLI v(x) = 0, TO
6	v		v2
d	u		= v du ; u dv :

(5.2.5)

(5.2.6)

(5.2.7)

wO WSEH \TIH RAWENSTWAH PREDPOLAGAETSQ, ^TO FUNKCII u I v DIFFERENCIRUEMY W NEKOTOROJ TO^KE, I UTWERVDAETSQ SU]ESTWOWA- NIE W \TOJ TO^KE DIFFERENCIALOW FUNKCIJ, POLU^ENNYH IZ u I v S POMO]X@ ARIFMETI^ESKIH DEJSTWIJ, I DA@TSQ WYRAVENIQ DLQ \TIH DIFFERENCIALOW.

dOKAZATELXSTWO RAWENSTW (5.2.5){(5.2.7) PROWODITSQ ODNOTIPNO. nAPRIMER, W SILU (5.2.3) I FORMULY DLQ PROIZWODNOJ PROIZWEDENIQ IMEEM

d(u v) = (u v)0dx = u0 vdx + u v0dx = du v + u dv:

wYQSNIM GEOMETRI^ESKIJ SMYSL PROIZWODNOJ I DIFFERENCIALA. sNA^ALA RASSMOTRIM, KAKOMU SWOJSTWU GRAFIKA FUNKCII SOOT-

WETSTWUET SU]ESTWOWANIE PROIZWODNOJ.

pUSTX FUNKCIQ f NEPRERYWNA W TO^KE x0. bUDEM PRIDAWATX ARGU- MENTU x0 TAKIE PRIRA]ENIQ x, ^TOBY TO^KI x0 + x NE WYHODILI ZA OBLASTX OPREDELENIQ FUNKCII f.

92

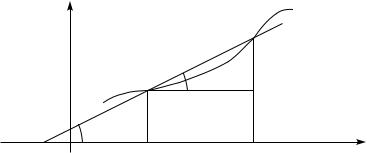
oTMETIM NA GRAFIKE FUNKCII f TO^KI A(x0 f(x0)) I B(x0 +x f(x0 + x)) I PROWEDEM ^EREZ \TI TO^KI PRQMU@. pUSTX | UGOL, KOTORYJ OBRAZUET PRQMAQ AB S OSX@ ABSCISS OX. uGOL S^ITAEM POLOVITELXNNYM, ESLI PRQMAQ AB PRAWEE TO^KI PERESE^E- NIQ S OSX@ OX LEVIT WY[E OSI, A W PROTIWNOM SLU^AE S^ITAEM OTRICATELXNYM. eSLI PRQMAQ AB PARALLELXNA OSI ABSCISS OX, TO POLAGAEM = 0.

y	y=f(x)
	B
	y

Aα

		x
α
x	0	x + x	x
		0

tAK KAK y = f(x0 + x)) ; f(x0), TO IZ RISUNKA WIDNO, ^TO

	y	= tg :	(5.2.8)
	x

w SILU NEPRERYWNOSTI FUNKCII f W TO^KE x0 TO^KA B GRAFIKA FUNKCII PRI x ! 0 NEOGRANI^ENNO PRIBLIVAETSQ K TO^KE A. pRI \TOM ZNA^ENIE UGLA ZAWISIT OT x.

rAWENSTWO (5.2.8) POKAZYWAET, ^TO SU]ESTWOWANIE PROIZWODNOJ FUNKCII f W TO^KE x0 RAWNOSILXNO SU]ESTWOWANI@ PREDELA tg PRIx ! 0. tAK KAK TANGENS QWLQETSQ NEPRERYWNOJ FUNKCIEJ, TO SU- ]ESTWOWANIE PREDELA tg RAWNOSILXNO SU]ESTWOWANI@ PREDELXNOGO ZNA^ENIQ UGLA , KOTOROE OBOZNA^IM 0. a \TO W SWO@ O^EREDX OZNA- ^AET, ^TO PRI x ! 0 SEKU]AQ AB ZANIMAET PREDELXNOE POLOVE- NIE, SOOTWETSTWU@]EE UGLU NAKLONA 0. pRQMU@, POLU^ENNU@ KAK PREDELXNOE POLOVENIE SEKU]EJ, NAZYWA@T KASATELXNOJ K GRAFIKU FUNKCII f(x) W TO^KE x0. pRI \TOM

f0(x0) = tg 0:

iTAK, SU]ESTWOWANIE PROIZWODNOJ RAWNOSILXNO SU]ESTWOWANI@ KASATELXNOJ K GRAFIKU FUNKCII, KAK PREDELXNOGO POLOVENIQ SEKU- ]EJ, A ZNA^ENIE PROIZWODNOJ RAWNO TANGENSU UGLA NAKLONA KASATELX- NOJ.

zAMETIM, ^TO W \TIH RASSUVDENIQH MOVNO BYLO IMETX W WIDU ODNOSTORONNIE PROIZWODNYE.

93

fIZI^ESKIJ SMYSL PROIZWODNOJ | \TO SKOROSTX IZMENENIQ ZAWI- SIMOJ PEREMENNOJ y KAK FUNKCII NEZAWISIMOJ PEREMENNOJ x. eSLI y | PUTX, PROJDENNYJ TO^KOJ PRI DWIVENII PO PRQMOJ, A x | WRE- MQ, TO PROIZWODNAQ | \TO SKOROSTX DWIVENIQ.

w FIZIKE PROIZWODNU@ NAZYWA@T MGNOWENNOJ SKOROSTX@ W OT- LI^IE OT SREDNEJ SKOROSTI ZA OPREDELENNYJ PROMEVUTOK WREMENI, KOTORAQ RAWNA OTNO[ENI@ PRIRA]ENIQ FUNKCII K PRIRA]ENI@ AR- GUMETNA.

wOOB]E, ESLI FUNKCIQ OPISYWAET NEKOTORYJ PROCESS, TO PROIZ- WODNAQ HARAKTERIZUET MGNOWENNU@ SKOROSTX PROTEKANIQ \TOGO PRO- CESSA.

dIFFERENCIAL FUNKCII RAWEN PRIRA]ENI@ ORDINATY KASATELX- NOJ PRI ZADANNOM x. tAKIM OBRAZOM, DIFFERENCIAL | \TO LINEJ- NAQ FUNKCIQ, GRAFIKOM KOTOROJ QWLQETSQ KASATELXNAQ. dIFFERE- NIAL POKAZYWAET, KAK MENQLASX BY FUNKCIQ, ESLI W TE^ENIE WSEGO WREMENI IZMENENIE FUNKCII PROHODILO BY S TOJ VE SKOROSTX@, ^TO I DANNYJ MOMENT.

pRIMENENIE DIFFERENCIALOW OPIRAETSQ NA TO, ^TO \W MALOM", T.E. PRI DOSTATO^NO MALYH x, PRIRA]ENIE FUNKCII NEZNA^ITELX- NO OTLI^AETSQ OT PRIRA]ENIQ LINEJNOJ FUNKCII, T.E. OT DIFFE- RENCIALA I, ZNA^IT, DIFFERENCIAL DAET HORO[EE PRIBLIVENIE DLQ PRIRA]ENIQ FUNKCII.

x 5.3. pROIZWODNAQ OBRATNOJ FUNKCII

pUSTX NA INTERWALE (a b) ZADANA NEPRERYWNAQ STROGO MONOTON- NAQ FUNKCIQ y = f(x).

oBOZNA^IM ^EREZ (A B) OBRAZ INTERWALA (a b) PRI OTOBRAVENII, OSU]ESTWLQEMOM FUNKCIEJ f. tOGDA SOGLASNO TEOREME 4.5.2 NA (A B) OPREDELENA NEPRERYWNAQ STROGO MONOTONNAQ OBRATNAQ FUNKCIQ x =

'(y).

wYQSNIM, KAK SWQZANY DIFFERENCIRUEMOSTX ISHODNOJ FUNKCII f W TO^KE x0 I DIFFERENCIRUEMOSTX OBRATNOJ FUNKCII ' W TO^KE y0 := f(x0).

bUDEM RASSMATRIWATX TAKIE PRIRA]ENIQ ARGUMENTA x, PRI KO- TORYH TO^KI x0 + x PRINADLEVAT INTERWALU (a b). tOGDA W SILU NEPRERYWNOSTI FUNKCII f W TO^KE x0 IZ x ! 0 SLEDUET y =

f(x0 + x) ; f(x0) ! 0.

eSLI ARGUMENTU y OBRATNOJ FUNKCII '(y) DAWATX TAKIE PRIRA- ]ENIQ, PRI KOTORYH TO^KI y0+ y NE WYHODQT ZA PREDELY INTERWALA (A B), TO DLQ PRIRA]ENIJ x, KOTORYE BUDET POLU^ATX FUNKCIQ ', W SILU NEPRERYWNOSTI OBRATNOJ FUNKCII POLU^IM, ^TO IZ y ! 0 SLEDUET x ! 0.

94

tAKIM OBRAZOM, W NA[EM SLU^AE USLOWIQ x RAWNOSILXNY.

! 0 I y ! 0

pREDPOLOVIM, ^TO SU]ESTWUET PROIZWODNAQ f0(x0), I RASSMOT- RIM WOPROS O SU]ESTWOWANII PROIZWODNOJ '0(y0).

pRI DOSTATO^NO MALYH PRIRA]ENIQH ARGUMENTA y FUNKCIQ ' POLU^AET PRIRA]ENIE x = '(y0 + y) ; '(y0) I SU]ESTWOWANIE PROIZWODNOJ '0(y0) RAWNOSILXNO SU]ESTWOWANI@ PREDELA

lim x :

y!0 y

tAK KAK FUNKCIQ ' STROGO MONOTONNA, TO IZ y = 0 SLEDUET
x = 0. pO\TOMU		6
6
x	y
y	= 1 : x :	(5.3.1)

eSLI f0(x0) 6= 0, TO POLXZUQSX RAWNOSILXNOSTX@ USLOWIJ y ! 0
I x ! 0, IZ (5.3.1) NAHODIM
lim	x =	lim	1 :	y	=	1		=	1	:
				x			y		0
y!0	y	x!0				lim x!0	x		f (x0)

tAKIM OBRAZOM, DOKAZANO SLEDU@]EE UTWERVDENIE.

tEOREMA 5.3.1. eSLI NEPRERYWNAQ FUNKCIQ f(x) STROGO MONOTONNA W NEKOTOROJ OKRESTNOSTI TO^KI x0, IMEET W \TOJ TO^KE PROIZWODNU@ I f0(x0) 6= 0, TO OBRATNAQ FUNKCIQ '(y) IMEET W TO^KE y0 = f(x0) PROIZWODNU@ I SPRAWEDLIWO RAWENSTWO

'0(y0) =	1	:	(5.3.2)
	f0(x0)

eSLI f0(x0) = 0, TO FORMULA (5.3.2) NE IMEET SMYSLA. wYQSNIM, ^TO MOVNO SKAZATX O PROIZWODNRJ OBRATNOJ FUNKCII W \TOM SLU^AE. eSLI FUNKCIQ f STROGO WOZRASTAET, TO PRIRA]ENIQ y I x

IME@T ODINAKOWYE ZNAKI. pO\TOMU IH OTNO[ENIE POLOVITELXNO I,
PEREHODQ W (5.3.1) K PREDELU PRI y ! 0 (ILI, ^TO TO VE SAMOE, PRI
x ! 0), WIDIM, ^TO
lim	x =	lim	1	= +	1	:
y!0	y	x!0	y= x

a ESLI FUNKCIQ f STROGO UBYWAET, TO OTNO[ENIE PRIRA]ENIJy I x OTRICATELXNO. zNA^IT, W \TOM SLU^AE

x

y!0

lim y = ;1:

95

tAKIM OBRAZOM, MOVNO S^ITATX, ^TO FORMULA (5.3.2) IMEET MESTO I PRI f0(x0) = 0, ESLI DOGOWORITXSQ, ^TO W \TOM SLU^AE ONA OZNA^AET SU]ESTWOWANIE BESKONE^NOJ PROIZWODNOJ '0(y0), RAWNOJ +1 ILI ;1 W ZAWISIMOSTI OT TOGO, WOZRASTAET ILI UBYWAET FUNKCIQ f.

w SOOTWETSTWII S \TIM S^ITA@T, ^TO ESLI SU]ESTWUET ODNA IZ PROIZWODNYH f0(x0) ILI '0(y0), KONE^NAQ ILI BESKONE^NAQ, TO SU- ]ESTWUET I WTORAQ I IH ZNA^ENIQ SWQZANY SOOTNO[ENIEM (5.3.2).

wOSPOLXZUEMSQ FORMULOJ PROIZWODNOJ OBRATNOJ FUNKCII DLQ WY^ISLENIQ PROIZWODNYH \LEMENTARNYH FUNKCIJ.

zAMETIM, ^TO TAK KAK POKAZATELXNAQ FUNKCIQ y = ax I LOGA-

RIFMI^ESKAQ FUNKCIQ y = loga x QWLQ@TSQ WZAIMNO OBRATNYMI, TO FORMULU DLQ PROIZWODNOJ ODNOJ IH \TIH FUNKCIJ MOVNO POLU^ITX IZ FORMULY DLQ DRUGOJ FUNKCII.

pOLU^IM, NAPRIMER, IZ RAWENSTWA (ax)0

= ax ln a FORMULU DLQ

PROIZWODNOJ LOGARIFMI^ESKOJ FUNKCII.

eSLI y = loga x, TO x = ay. pO\TOMU SOGLASNO (5.3.2) IMEEM

(loga x)0 =

1

=

1

=

1

:

(ay)0

ay ln a

x ln a

nAJDEM PROIZWODNYE OBRATNYH TRIGONOMETRI^ESKIH FUNKCIJ.

1 . eSLI y = arcsin x, TO x = sin y. pO\TOMU

1

1

1

1

(arcsin x)0 =

=

=

=

p

:

(5.3.3)

(sin y)0

cos y

1 ; sin2 y

1 ; x2

p

2 . aNALOGI^NO WY^ISLQETSQ PROIZWODNAQ FUNKCII y = arccos x.

iMEEM x = cos y I

1

1

1

1

(arccos x)0 =

= ;

= ;

= ;

:

(5.3.4)

(cos y)0

sin y

p

1;cos2 y

1;x2

p

2

;

fORMULY (5.3.3) I (5.3.4) SPRAWEDLIWY DLQ WSEH x

[

1 1]. oNI

POKAZYWA@T, ^TO PRI x = 1 SU]ESTWU@T BESKONE^NYE ODNOSTORON-

NIE PROIZWODNYE.

3 . eSLI y = arctg x, TO x = tg y I SOGLASNO (5.3.2)

1

cos2 y

1

1

(arctg x)0 =

= cos2 y =

=

=

:

(tg y)0

cos2 y+ sin2 y

1+ tg2 y

1+x2

(5.3.5)

4 . aNALOGI^NO DLQ y = arcctg x NAHODIM

(arcctg x)0 =

1

= ;sin2 y =

(ctg y)0

(5.3.6)

sin2 y

1

1

= ;

= ;

= ;

:

sin2 y + cos2 y

1 + ctg2 y

1 + x2

96

fORMULY (5.3.5) I (5.3.6) IME@T MESTO DLQ WSEH x.

x 5.4. pROIZWODNAQ SLOVNOJ FUNKCII

tEOREMA 5.4.1. pUSTX FUNKCIQ y = f(x) IMEET PROIZWODNU@ W TO^KE x0, y0 := f(x0) I FUNKCIQ z = '(y) IMEET PROIZWODNU@ W TO^KE y0. tOGDA SLOVNAQ FUNKCIQ z = (x) := '(f(x)) IMEET PROIZWODNU@ W TO^KE x0 I SPRAWEDLIWO RAWENSTWO

0(x0) = '0(y0) f0(x0):	(5.4.1)
dOKAZATELXSTWO. sU]ESTWOWANIE SLOVNOJ FUNKCII	(x) SOGLASNO

SKAZANNOMU W x4.1 WYTEKAET IZ NEPRERYWNOSTI FUNKCIJ f(x) I '(y). iZ USLOWIJ TEOREMY SLEDUET, ^TO DLQ PRIRA]ENIJ FUNKCIJ f I

' W TO^KAH x0 I y0 SOOTWETSTWENNO SPRAWEDLIWY RAWENSTWA
y = f0(x0) x + x "( x)	(5.4.2)
I
z = '0(y0) y + y "1( y)	(5.4.3)

GDE "( x) ! 0 PRI x ! 0 I "1( y) ! 0 PRI y ! 0.

~TOBY WYRAZITX PRIRA]ENIE z ^EREZ x, PODSTAWIM W PERWOE

SLAGAEMOE IZ PRAWOJ ^ASTI FORMULY (5.4.3) WMESTO y EGO PREDSTAW- LENIE IZ (5.4.2). zNA^ENIE y, NAJDENNOE PO FORMULE (5.4.2), MOVET OKAZATXSQ RAWNYM NUL@. kAK GOWORILOSX W x5.2, S^ITAEM "1(0) = 0.

tOGDA POLU^IM

z = '0(y0) ;f0(x0) x + x "( x) + y "1( y) = = '0(y0) f0(x0) x + '0 (y0) x "( x) + y "1( y):

rAZDELIM LEWU@ I PRAWU@ ^ASTI \TOGO RAWENSTWA NA x:

z	= '0(y0) f0(x0) + '0(y0) "( x) +	y	"1( y):	(5.4.4)
x		x

eSLI x ! 0, TO y ! 0. pO\TOMU PEREHOD W (5.4.4) K PREDELU PRI x ! 0 PRIWODIT K RAWENSTWU

lim z = '0(y0) f0(x0):

x!0 x

tAKIM OBRAZOM, DOKAZANY I SU]ESTWOWANIE PROIZWODNOJ 0(x0) I RAWENSTWO (5.4.1).

97

y = eln xa

dLQ OBOZNA^ENIQ ZNA^ENIQ PROIZWODNOJ FUNKCII y = f(x) W TO^-
KE x0 UPOTREBLQETSQ TAKVE ZAPISX yx0 (x0). w \TIH OBOZNA^ENIQH FOR-
MULA DLQ PROIZWODNOJ SLOVNOJ FUNKCII IMEET WID
zx0 (x0) = zy0 (y0) yx0 (x0):	(5.4.5)

pRIWEDEM PRIMERY PRIMENENIQ FORMULY PROIZWODNOJ SLOVNOJ FUNKCII.

1 . nAJDEM PROIZWODNU@ STEPENNOJ FUNKCII y = xa, x > 0, GDE a | PROIZWOLXNOE ^ISLO. w x5.1 PROIZWODNAQ STEPENNOJ FUNKCII BYLA WY^ISLENA W SLU^AE, KOGDA a | CELOE ^ISLO. tOGDA PRI a > 0 ARGUMENT x MOG BYTX L@BYM, A PRI a < 0 | L@BYM NE RAWNYM NUL@ ^ISLOM.

iMEEM

= ea ln x:

pOLOVIM u = a ln x. tOGDA y = eu I, ZNA^IT, SOGLASNO (5.4.5)

0 0 0 u a	a ln x a			a a		a;1
yx = yu ux = e x	= e	x	= x	x	= ax		:	(5.4.6)

fORMULA (5.4.6) DLQ PROIZWOLXNYH a IMEET MESTO PRI x > 0, A ESLI a > 1, TO ONA SPRAWEDLIWA I PRI x = 0. zAMETIM, ^TO DLQ 0 < a < 1 STEPENNAQ FUNKCIQ y = xa IMEET W NULE PRAWU@ BESKONE^NU@ PROIZWODNU@.

pRIWEDENNOE DOKAZATELXSTWO FORMULY (5.4.6) NE ZAWISIT OT TOGO, QWLQETSQ ^ISLO a CELYM ILI NET. nO DLQ SLU^AQ, KOGDA a | NATU- RALXNOE ^ISLO, \TO DOKAZATELXSTWO NE POZWOLQET NAJTI PROIZWODNU@ DLQ OTRICATELXNYH x W OTLI^IE OT FORMULY (5.1.7), KOTORAQ W \TOM SLU^AE IMEET MESTO DLQ WSEH x.

2 . nAJDEM PROIZWODNU@ FUNKCII y = loga jxj, x =6 0.

~TOBY WOSPOLXZOWATXSQ FORMULOJ PROIZWODNOJ SLOVNOJ FUNK-

CII, POLOVIM u = jxj. tOGDA y = loga u.

wWEDEM FUNKCI@, NAZYWAEMU@ sign x (OT LATINSKOGO signum) ILI

ZNAK x:

+1

ESLI x > 0

>

sign x := 80

ESLI x = 0

<;1

ESLI x < 0:

tOGDA u =

j

x

j

= x

sign>x I

j

x

0 = sign x PRI x = 0. pO\TOMU

:

j

6

SOGLASNO (5.4.5)

y0 = y0

u0 =

1

sign x = sign x

1

=

1

:

x

u

x

u ln a

jxj

ln a x ln a

98

tAKIM OBRAZOM,

(log

a j

x

)0 =

1

x = 0:

(5.4.7)

x ln a

j

6

w ^ASTNOSTI,

(ln

j

x

)0

=

1

x = 0:

(5.4.8)

j

x

6

rAZUMEETSQ,

PROIZWODNU@ FUNKCII loga jxj

MOVNO BYLO NAJTI,

NE PRIBEGAQ K FORMULE PROIZWODNOJ SLOVNOJ FUNKCII.

3 . wY^ISLIM PROIZWODNYE GIPERBOLI^ESKIH SINUSA I KOSINUSA:

(sh x)0 = e

x

; e

;x 0

x

;

;x

0

x

;x

= e

(e

)

=

e + e

= ch x

(5.4.9)

2

x

2

2

;x

0

x

;x

(ch x)0

=

e + e

= e

; e

= sh x:

(5.4.10)

2

2

tAKIM OBRAZOM, NAJDENY PROIZWODNYE WSEH OSNOWNYH \LEMENTAR- NYH FUNKCIJ.

x 5.5. pROIZWODNYE I DIFFERENCIALY WYS[IH PORQDKOW

eSLI FUNKCIQ f(x) IMEET PROIZWODNU@ f0(x) WO WSEH TO^KAH IZ NEKOTOROJ OKRESTNOSTI TO^KI x0, TO MOVNO POSTAWITX WOPROS O SU- ]ESTWOWANII W \TOJ TO^KE PROIZWODNOJ FUNKCII f0(x). eSLI f0(x) IMEET PROIZWODNU@ W TO^KE x0, TO \TU PROIZWODNU@ NAZYWA@T WTO- ROJ PROIZWODNOJ FUNKCII f(x) W TO^KE x0 I OBOZNA^@T f00(x0).

aNALOGI^NO OPREDELQ@TSQ TRETXQ PROIZWODNAQ I WOOB]E PROIZ- WODNYE L@BOGO PORQDKA.

pROIZWODNAQ f(n) PORQDKA n FUNKCII f(x) SU]ESTWUET W TO^KE x0, ESLI W NEKOTOROJ OKRESTNOSTI \TOJ TO^KI SU]ESTWUET PROIZWOD- NAQ PORQDKA n ;1 FUNKCII f(x), T.E. SU]ESTWUET f(n;1)(x), I FUNK-

CIQ f(n;1)(x) IMEET PROIZWODNU@ W TO^KE x0. |TU PROIZWODNU@ OBO-

ZNA^A@T f(n)(x0) I NAZYWA@T PROIZWODNOJ PORQDKA n FUNKCII f(x)

W TO^KE x0.

oSNOWNYE \LEMENTARNYE FUNKCII IME@T PROIZWODNYE L@BOGO PORQDKA W SWOEJ ESTESTWENNOJ OBLASTI OPREDELENIQ. nAPRIMER,

(ax)(n) = ax (ln a)n (sin x)(n) = sin x + n2

99

(xa)(n) = a(a ; 1) : : : (a ; n + 1)xa;n:

w SWQZI S FORMULOJ DLQ PROIZWODNOJ STEPENNOJ FUNKCII OTME- TIM, ^TO ESLI ^ISLO a > 0 NE CELOE, TO FUNKCIQ xa W NULE IMEET PROIZWODNYE DO PORQDKA [a] WKL@^ITELXNO, NO NE IMEET PROIZWOD- NYH BOLEE WYSOKOGO PORQDKA.

eSLI FUNKCIQ IMEET W TO^KE ILI NA NEKOTOROM PROMEVUTKE PRO- IZWODNYE WSEH PORQDKOW, TO \TU FUNKCI@ NAZYWA@T BESKONE^NO DIF- FERENCIRUEMOJ SOOTWETSTWENNO W TO^KE ILI NA PROMEVUTKE.

fUNKCIQ MOVET IMETX PROIZWODNU@ PERWOGO PORQDKA, NO NE IMETX PROIZWODNOJ WTOROGO PORQDKA. nAPRIMER, ESLI y = xjxj, TO

y0 = 2jxj I, ZNA^IT, \TA FUNKCIQ NE IMEET W NULE PROIZWODNOJ WTO- ROGO PORQDKA.

tO^NO TAKVE MOVNO UKAZATX FUNKCII, IME@]IE PROIZWODNU@ PORQDKA n > 1, NO NE IME@]IE PROIZWODNOJ PORQDKA n + 1.

eSLI FUNKCII u(x) I v(x) IME@T W NEKOTOROJ TO^KE PROIZWODNYE PORQDKA n, TO QSNO, ^TO SUMMA I RAZNOSTX \TIH FUNKCIJ TAKVE IME- @T W \TOJ TO^KE PROIZWODNYE PORQDKA n I WYPOLNQ@TSQ RAWENSTWA

(u(x) v(x))(n) = u(n)(x) v(n)(x):

w \TOM LEGKO UBEDITXSQ PO INDUKCII.

rASSUVDENIQ PO INDUKCII POKAZYWA@T TAKVE, ^TO PRI \TIH USLOWIQH SU]ESTWUET PROIZWODNAQ PORQDKA n PROIZWEDENIQ u(x)v(x). sEJ^AS NAS BUDET INTERESOWATX WYRAVENIE PROIZWODNYH WYS[IH PORQDKOW OT PROIZWEDENIQ FUNKCIJ ^EREZ PROIZWODNYE SAMIH \TIH

FUNKCIJ.

zDESX POTREBU@TSQ WELI^INY

Cnk :=	n!	0 6 k 6 n	0! := 1	(5.5.1)

k! (n ; k)!

KOTORYE NAZYWA@T BINOMIALXNYMI KO\FFICIENTAMI, TAK KAK \TI

^ISLA U^ASTWU@T W FORMULE BINOMA nX@TONA, NO OB \TOM BUDET GO- WORITXSQ POZDNEE.

~ISLO Cnk NAZYWA@T ^ISLOM SO^ETANIJ IZ n PO k, TAK KAK ONO POKAZYWAET, SKOLXKO RAZLI^NYH PODMNOVESTW, SOSTOQ]IH IZ k \LE- MENTOW, IMEET MNOVESTWO IZ n \LEMENTOW. nO \TO SWOJSTWO SEJ^AS NE BUDET NUVNO.

tEOREMA 5.5.1 (fORMULA lEJBNICA). eSLI FUNKCII u(x) I v(x)

IME@T W TO^KE x0 PROIZWODNYE PORQDKA n, TO W \TOJ TO^KE SU- ]ESTWUET PROIZWODNAQ PORQDKA n PROIZWEDENIQ u(x) v(x) I SPRAWEDLIWO RAWENSTWO

	n
(u(x0) v(x0))(n) =	X	Ck u(k)(x0) v(n;k)(x0) n = 1 2 : : : (5.5.2)
		n
	k=0

100