Матан, Лекции - Теляковский 1

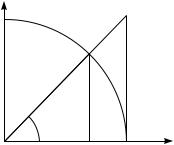
y

D

B

x

O		C				A	x
pLO[ADX KRUGOWOGO SEKTORA OAB RAWNA R2x=2. pO\TOMU
R2 x	< 1 R2 tg x
2	2
OTKUDA SLEDUET, ^TO x < tg x, I, ZNA^IT,
cos x <			sin x			:
			x
w SILU (4.7.1) sin x < x. tAKIM OBRAZOM,
cos x <		sin x			< 1:
		x

tAK KAK WSE FUNKCII W \TOM NERAWENSTWE ^ETNYE, TO ONO IMEET

MESTO I PRI x 2 (; =2 0).
w SILU NEPRERYWNOSTI FUNKCII KOSINUS, ESLI x ! 0, TO cos x !
1. pO\TOMU SOGLASNO TEOREME 3.3.4
lim	sin x	= 1:	(4.8.2)
x!0	x

dALEE BUDET NUVNA NOWAQ FUNKCIQ | CELAQ ^ASTX ^ISLA. oBY^NO \TU FUNKCI@ OBOZNA^A@T [x], INOGDA E(x).

pO OPREDELENI@

[x] :=	max	n:
	n6x n2Z
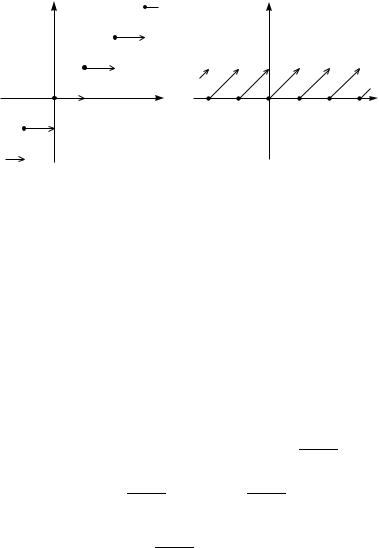
gRAFIK FUNKCII [x] IZOBRAVEN NA RISUNKE.
2 . pOKAVEM, ^TO
lim (1 + x)1=x		= e:	(4.8.3)
x!0

dLQ x = 1=n, n ! 1, W x2.6 BYLO DOKAZANO, ^TO TAKOJ PREDEL SU]ESTWUET. oN BYL WZQT W KA^ESTWE OPREDELENIQ ^ISLA e.

81

	y
	2
	1
–1	0	1	2	3	x
		–1
				y=[x]
eSLI x > 0, TO

	y
–1	0	1	2	3	x
		y={x}:=x–[x]

(1 + x)1=x = 1 +		1			1=x	6 1 +	1				[1=x]+1
											=
		1=x						[1=x]
		1		[1=x]			1
= 1 +						1 +
	[1=x]						[1=x]

A PREDEL POSLEDNEGO WYRAVENIQ PRI x ! +0 RAWEN e. s DRUGOJ STORONY,

		1		[1=x]	1		[1=x]+1	1	;1
	(1+x)1=x > 1+			> 1+			1+		:
		1=x			[1=x] + 1			[1=x] + 1

pRI x ! +0 PREDEL POLU^ENNOGO WYRAVENIQ TAKVE RAWEN e I, TAKIM

OBRAZOM, W SILU TEOREMY 3.3.4 RAWENSTWO (4.8.3) DOKAZANO DLQ x !

+0.

pUSTX TEPERX x < 0. tOGDA

1

1=jxj

jxj

1=jxj

(1 + x)1=x = (1

x );1=jxj =

=

1 +

=

1

; jxj

; j j

1 ; jxj

1;jxj

jxj

jxj

jxj

=

1 +

1 +

:

1 ; jxj

1 ; jxj

nO ESLI x ! 0, TO

1 jxjx

j

! 0:

; j

pO\TOMU W SILU DOKAZANNOGO UVE RAWENSTWA (4.8.3) DLQ x > 0 POLU-

^AEM, ^TO ONO IMEET MESTO I DLQ x < 0.

3 . pUSTX a > 0 I a = 1. nAJDEM PREDEL

6

loga(1 + x)

lim

:

x

x!0

82

pOLXZUQSX NEPRERYWNOSTX@ LOGARIFMI^ESKOJ FUNKCII I RAWEN- STWOM (4.8.3), POLU^AEM

lim

loga(1 + x)

= lim loga(1 + x)

1=x

=

x

x!0

x!0

= loga

lim (1 + x)1=x = loga e =

1

:

ln a

;

x!0

tAKIM OBRAZOM,

lim

loga(1 + x)

=

1

(4.8.4)

x

ln a

x!0

W ^ASTNOSTI,

lim

ln(1 + x)

= 1:

(4.8.5)

x!0

x

4 . wY^ISLIM PREDEL

lim

ax ; 1

x!0

x

DLQ a > 0 I a = 1.

pOLOVIM a6x

;

1 = t. tOGDA ax = 1 + t I x = loga(1 + t). zNA^IT,

ax ; 1 =

t

:

loga(1 + t)

x

w SILU NEPRERYWNOSTI POKAZATELXNOJ FUNKCII t ! 0 PRI x ! 0. pO\TOMU, POLXZUQSX RAWENSTWOM (4.8.4), NAHODIM

lim ax ; 1		= ln a:		(4.8.6)
x!0	x
w ^ASTNOSTI,
lim	ex ; 1		= 1:	(4.8.7)
x!0	x

gLAWA 5

proizwodnye i differencialy

x 5.1. pROIZWODNAQ

pUSTX FUNKCIQ y = f(x) OPREDELENA W NEKOTOROJ OKRESTNOSTI TO^KI x0. pRIDADIM ARGUMENTU x0 DOSTATO^NO MALOE PRIRA]ENIE

83

x, ^TOBY NE WYJTI IZ OBLASTI OPREDELENIQ FUNKCII, I RASSMOT- RIM PRIRA]ENIE FUNKCII f, SOOTWETSTWU@]EE \TOMU PRIRA]ENI@ ARGUMENTA:

y = f := f(x0 + x)		; f(x0):
sOSTAWIM OTNO[ENIE PRIRA]ENIQ FUNKCII K PRIRA]ENI@ ARGU-
MENTA I POSTAWIM WOPROS O SU]ESTWOWANII PREDELA \TOGO OTNO[ENIQ
PRI x ! 0.
oPREDELENIE. eSLI SU]ESTWUET PREDEL
lim	y	(5.1.1)
x!0	x

TO ZNA^ENIE \TOGO PREDELA NAZYWA@T PROIZWODNOJ FUNKCII f W TO^- KE x0, OBOZNA^A@T f0(x0) I GOWORQT, ^TO FUNKCIQ f IMEET W TO^KE x0 PROIZWODNU@.

tEOREMA 5.1.1. eSLI FUNKCIQ f W NEKOTOROJ TO^KE IMEET PROIZWODNU@, TO f NEPRERYWNA W \TOJ TO^KE.

dOKAZATELXSTWO. iZ SU]ESTWOWANIQ PREDELA (5.1.1) SLEDUET, ^TO W DOSTATO^NO MALOJ OKRESTNOSTI TO^KI x0 SPRAWEDLIWO RAWENSTWO

	y	= f0	(x0) + "( x)	(5.1.2)
	x
GDE "( x) | NEKOTORAQ FUNKCIQ OT x TAKAQ, ^TO
		lim	"( x) = 0:	(5.1.3)
	x!0

w SILU (5.1.2)

y = f0(x0) x + "( x) x:

pRI x ! 0 WYRAVENIE IZ PRAWOJ ^ASTI \TOGO RAWENSTWA STRE- MITSQ K NUL@, T.E. y ! 0, A \TO OZNA^AET NEPRERYWNOSTX FUNKCII

f W TO^KE x0. tEOREMA DOKAZANA.

tAKIM OBRAZOM, NEOBHODIMYM USLOWIEM SU]ESTWOWANIQ PROIZ- WODNOJ FUNKCII W TO^KE QWLQETSQ NEPRERYWNOSTX FUNKCII W \TOJ TO^KE. nO \TO USLOWIE NE QWLQETSQ DOSTATO^NYM.

w SAMOM DELE, PUSTX y := jxj. tOGDA DLQ PRIRA]ENIQ FUNKCII W
NULE SPRAWEDLIWO RAWENSTWO y = j xj I, SLEDOWATELXNO,
y	1	ESLI x > 0
x	= (;1	ESLI x < 0:	(5.1.4)

84

zNA^IT, FUNKCIQ jxj NE IMEET PROIZWODNOJ W NULE, HOTQ ONA I NE- PRERYWNA WS@DU.

zAMETIM, ^TO W DANNOM PRIMERE SU]ESTWU@T ODNOSTORONNIE PRE- DELY OTNO[ENIQ PRIRA]ENIQ FUNKCII K PRIRA]ENI@ ARGUMENTA (5.1.4). w TAKIH SLU^AQH GOWORQT OB ODNOSTORONNIH PROIZWODNYH.

oPREDELENIE. pUSTX FUNKCIQ f OPREDELENA W NEKOTOROJ PRAWOJ OKRESTNOSTI TO^KI x. eSLI SU]ESTWUET ODNOSTORONNIJ PREDEL

lim	y		(5.1.5)
x!+0	x

TO GOWORQT, ^TO FUNKCIQ f IMEET W TO^KE x PRAWU@ ODNOSTORONN@@ PROIZWODNU@ f+0 (x), RAWNU@ ZNA^ENI@ PREDELA (5.1.5).

eSLI FUNKCIQ f OREDELENA W NEKOTOROJ LEWOJ OKRESTNOSTI TO^KI x I SU]ESTWUET ODNOSTORONNIJ PREDEL

lim	y		(5.1.6)
x!;0	x

TO GOWORQT, ^TO FUNKCIQ f IMEET W TO^KE x LEWU@ ODNOSTORONN@@ PROIZWODNU@ f;0 (x), RAWNU@ ZNA^ENI@ \TOGO PREDELA.

sLOWO \ODNOSTORONN@@" ZDESX ^ASTO OPUSKA@T I GOWORQT O PRA- WOJ PROIZWODNOJ ILI PROIZWODNOJ SPRAWA, SOOTWETSTWENNO, LEWOJ

PROIZWODNOJ I PROIZWODNOJ SLEWA.						IMEEM f0
tAKIM OBRAZOM, DLQ FUNKCII f(x) = x								(0) = 1 I
f;0 (0) = ;1.				j	j		+
pRIWEDEM PRIMER FUNKCII, NEPRERYWNOJ WS@DU, NO NE IME@]EJ
W NEKOTOROJ TO^KE ODNOSTORONNIH PROIZWODNYH.
pUSTX
	x sin	1		PRI x = 0
f(x) :=
	(0	x		6
				PRI x = 0:

tAK KAK jf(x)j 6 jxj, TO FUNKCIQ f NEPRERYWNA W NULE, A EE NE- PRERYWNOSTX W OSTALXNYH TO^KAH O^EWIDNA. dLQ PRIRA]ENIQ f W

NULE IMEEM

f = x sin 1x :

zNA^IT,

fx = sin 1x

I U FUNKCII f W NULE NE SU]ESTWU@T NE TOLXKO PROIZWODNAQ, NO I ODNOSTORONNIE PROIZWODNYE.

85

wYWEDEM PRAWILA WY^ISLENIQ PROIZWODNYH.

pUSTX FUNKCII u(x) I v(x) IME@T PROIZWODNYE W TO^KE x. tAK KAK \TI FUNKCII OPREDELENY W NEKOTOROJ OKRESTNOSTI TO^KI x, TO PRAWOMEREN WOPROS O SU]ESTWOWANII PROIZWODNYH FUNKCIJ, PO- LU^ENNYH W REZULXTATE ARIFMETI^ESKIH DEJSTWIJ NAD FUNKCIQMI u(x) I v(x).

tEOREMA 5.1.2. pUSTX W NEKOTOROJ TO^KE x FUNKCII u I v IME@T PROIZWODNYE. tOGDA W \TOJ TO^KE SU]ESTWU@T SLEDU@]IE PROIZWODNYE I WYPOLNQ@TSQ RAWENSTWA:

1 . (u(x) + v(x))0 = u0(x) + v0(x). 2 . (u(x) ; v(x))0 = u0(x) ; v0(x).

3 . (u(x) v(x))0 = u0(x) v(x) + u(x) v0(x).

4 . eSLI v(x) 6= 0, TO

u(x)		0 = u0	(x) v(x)		; u(x) v0(x)	:
v(x)				v2(x)
dOKAZATELXSTWO. 1 . iMEEM
(u + v) = u(x + x) + v(x + x) ; (u(x) + v(x)) = u + v:
pO\TOMU
(u + v)				= u	+ v :
		x		x	x

dROBI W PRAWOJ ^ASTI \TOGO RAWENSTWA IME@T PREDELY PRI x !
0, PO\TOMU
lim	(u + v)	=	lim	u	+	lim	v	= u0(x) + v0(x):
x!0	x		x!0	x		x!0	x

dOKAZATELXSTWO SWOJSTWA 2 ANALOGI^NO. 3 . iMEEM

(uv) = u(x + x)v(x + x) ; u(x)v(x):

tAK KAK u = u(x + x) ; u(x), TO u(x + x) = u(x) + u. pO\TOMU

(u v) = (u(x) + u)(v(x) + v) ; u(x) v(x) = = u v(x) + u(x) v + u v

I, TAKIM OBRAZOM,

(uv)	=	uv(x) + u(x)	v	+	u	v:
x		x	x		x

86

zNA^IT,

kAVDOE SLAGAEMOE, STOQ]EE W \TOM RAWENSTWE SPRAWA, PRI x ! 0 IMEET PREDEL, PRI^EM v ! 0 W SILU NEPRERYWNOSTI FUNKCII v.

lim	(u v) = u0(x) v(x) + u(x) v0(x):
x!0	x
4 . sNA^ALA RASSMOTRIM ^ASTNYJ SLU^AJ, KOGDA u(x)		1, T.E.
POLU^IM FORMULU DLQ PROIZWODNOJ DROBI 1=v(x).

tAK KAK FUNKCIQ v W TO^KE x NEPRERYWNA I v(x) 6= 0, TO v NE OBRA]AETSQ W NULX W NEKOTOROJ OKRESTNOSTI TO^KI x. pO\TOMU DLQ DOSTATO^NO MALYH PRIRA]ENIJ x IMEEM

1

=

1

1

= v(x) ; v(x + x)

=

; v

:

v

v(x + x) ; v(x)

v(x + x) v(x)

v(x + x) v(x)

oTS@DA

1

1

v

v : x = ;

:

v(x + x) v(x)

x

wYRAVENIE IZ PRAWOJ ^ASTI \TOGO RAWENSTWA IMEET PREDEL PRIx ! 0. zNA^IT, SU]ESTWUET PREDEL WYRAVENIQ IZ LEWOJ ^ASTI I, TAKIM OBRAZOM,

1 0 = ; v20 :

v v

tEPERX S POMO]X@ FORMULY DLQ PROIZWODNOJ PROIZWEDENIQ PO- LU^IM FORMULU DLQ PROIZWODNOJ ^ASTNOGO W OB]EM SLU^AE:

u(x)		0	1			0		1			v0(x)
v(x)			= u(x)				= u0	(x)		; u(x)
				v(x)					v(x)		v2(x)

I OSTALOSX TOLXKO PRIWESTI POLU^ENNYE DROBI K OB]EMU ZNAMENA- TEL@.

tEOREMA DOKAZANA.

wYWEDEM FORMULY DLQ PROIZWODNYH NEKOTORYH \LEMENTARNYH

FUNKCIJ.

1 . eSLI FUNKCIQ f RAWNA KONSTANTE, T.E. DLQ WSEH x PRINIMAET ODNO I TO VE ZNA^ENIE C, TO f = 0 I, TAKIM OBRAZOM, C0 = 0.

pO\TOMU DLQ PROIZWOLXNOJ FUNKCII u, IME@]EJ W TO^KE x PROIZ- WODNU@, S POMO]X@ FORMULY PROIZWODNOJ PROIZWEDENIQ POLU^AEM

(Cu(x))0 = Cu0(x):

87

kONE^NO, \TO LEGKO BYLO POLU^ITX I NEPOSREDSTWENNO, RASSMATRIWAQ PRIRA]ENIE FUNKCII Cu(x).

2 . rASSMOTRIM STEPENNU@ FUNKCI@ S CELYM POKAZATELEM, T.E. FUNKCI@ f(x) = xn, GDE n | CELOE ^ISLO.

pOKAVEM, ^TO

(xn)0 = nxn;1

(5.1.7)

GDE x | L@BOE, ESLI n > 1, I x | L@BOE NERAWNOE NUL@ ^ISLO, ESLI n < 0.

sNA^ALA USTANOWIM FORMULU DLQ NATURALXNYH n, PROWEDQ IN- DUKCI@ PO n.

pRI n = 1 IMEEM f = x, OTKUDA SLEDUET, ^TO x0 = 1.

bUDEM TEPERX S^ITATX FORMULU (5.1.7) DOKAZANNOJ DLQ POKAZATE- LQ n I DOKAVEM EE DLQ POKAZATELQ n + 1.

pO FORMULE PROIZWODNOJ PROIZWEDENIQ IMEEM

(xn+1)0 = (x xn)0 = xn + x nxn;1 = (n + 1)xn:

tAKIM OBRAZOM, RAWENSTWO (5.1.7) USTANOWLENO DLQ WSEH NATURALX- NYH n.

rASSMOTRIM SLU^AJ, KOGDA n | CELOE OTRICATELXNOE ^ISLO.

				;		6
pOLOVIM m :=					n. tOGDA m > 0 I DLQ x = 0
					xn =		1	:
							xm
pO FORMULE PROIZWODNOJ ^ASTNOGO IMEEM
1			0		(xm)0	mxm;1
(xn)0 =				= ; x2m = ;			x2m = ;mx;m;1 = nxn;1
	xm

I RAWENSTWO (5.1.7) DLQ CELYH OTRICATELXNYH POKAZATELEJ DOKAZANO. tAK KAK PO OPREDELENI@ STEPENNOJ FUNKCII S NULEWYM POKAZA- TELEM x0 1, TO (x0)0 = 0. pO\TOMU MOVNO S^ITATX, ^TO FORMULA (5.1.7) IMEET MESTO I PRI n = 0, ESLI USLOWITXSQ, ^TO W \TOM SLU^AE

PRAWAQ ^ASTX W (5.1.7) RAWNA NUL@.

w DALXNEJ[EM BUDET POKAZANO, ^TO RAWENSTWO (5.1.7) IMEET MESTO DLQ L@BYH, A NE TOLXKO CELYH POKAZATELEJ n.

3 . nAJDEM PROIZWODNU@ POKAZATELXNOJ FUNKCII y = ax. tAK KAK

y	= ax+ x ; ax	= ax a x ; 1
x	x	x

88

TO W SILU (4.8.6) IMEEM
lim	y	= ax lim	a x ; 1	= ax ln a:
x!0	x	x!0	x
tAKIM OBRAZOM,
(ax)0 = ax ln a			;1 < x < 1:		(5.1.8)
w ^ASTNOSTI, ESLI a = e, TO
		(ex)0 = ex:			(5.1.9)

4 . nAJDEM PROIZWODNU@ LOGARIFMI^ESKOJ FUNKCII y = loga x. pREOBRAZUEM PRIRA]ENIE FUNKCII, ^TOBY BYLO UDOBNO WOSPOLX-

ZOWATXSQ PREDELOM (4.8.4). iMEEM

y = loga(x + x) ; loga x = loga 1 + xx :

pO\TOMU

y	1		x	1						x	1
x =		loga 1 +	x =					loga 1 +		x	x
	x				( x)=x
OTKUDA W SILU (4.8.4) POLU^AEM
				1		1
		(loga x)0 = loga e x				=			:		(5.1.10)
								x ln a
w ^ASTNOSTI,
			(ln x)0	= 1 :							(5.1.11)
					x
rAWENSTWA (5.1.10) I (5.1.11) IME@T MESTO DLQ WSEH x > 0.
5 . nAJDEM PROIZWODNYE TRIGONOMETRI^ESKIH FUNKCIJ.
pUSTX y = sin x. tOGDA
						x				x
y = sin(x + x) ; sin x = 2 sin						2 cos x + 2 :

oTS@DA, POLXZUQSX FORMULOJ (4.8.2) I NEPRERYWNOSTX@ FUNKCII cos x, NAHODIM

lim

y

=

lim

2

sin

x

cos

x +

x

= cos x:

x

x

2

2

x!0

x!0

89

tAKIM OBRAZOM,

(sin x)0 = cos x:

(5.1.12)

aNALOGI^NO WY^ISLQETSQ PROIZWODNAQ FUNKCII y = cos x:

y = cos(x + x) ; cos x = 2 sin

;

x

sin x +

x

2

2

ZNA^IT,

lim

y

= lim

2

sin

x

sin

x + x

=

sin x:

;

2

;

x!0

x

x!0

x

2

iTAK,

(cos x)0

= ;sin x:

(5.1.13)

rAWENSTWA (5.1.12) I (5.1.13) IME@T MESTO DLQ WSEH x.

pROIZWODNYE TANGENSA I KOTANGENSA NAHODIM, POLXZUQSX FORMU- LOJ PROIZWODNOJ ^ASTNOGO I PROIZWODNYMI SINUSA I KOSINUSA:

(tg x)0 =

sin x

0

= cos x cos x ; sin x (;sin x) =

1

cos x

cos2 x

cos2 x

(5.1.14)

(ctg x)0 =

cos x

0

= ;sin x sin x ; cos x cos x

=

1

:

sin x

;sin2 x

sin2 x

(5.1.15)

kAVDAQ IZ FORMUL (5.1.14) I (5.1.15) SPRAWEDLIWA DLQ WSEH x, PRI KOTORYH OPREDELENY TANGENS I, SOOTWETSTWENNO, KOTANGENS.

wY^ISLENIE PROIZWODNYH DRUGIH \LEMENTARNYH FUNKCIJ TREBU- ET ZNANIQ SWOJSTW PROIZWODNYH, KOTORYE BUDUT USTANOWLENY POZD- NEE.

w OPREDELENII PROIZWODNOJ PREDEL (5.1.1) S^ITA@T KONE^NYM. nO INOGDA NUVNO RASSMATRIWATX I SLU^AI, KOGDA \TOT PREDEL RA- WEN +1 ILI ;1. tOGDA GOWORQT O SOOTWETSTWU@]EJ BESKONE^NOJ PROIZWODNOJ. kAK I DLQ PREDELOW FUNKCII, ESLI NE SKAZANO, ^TO PROIZWODNAQ MOVET BYTX BESKONE^NOJ, TO S^ITA@T, ^TO \TA PROIZ- WODNAQ KONE^NA.

90