Матан, Лекции - Теляковский 1

GDE PO OPREDELENI@ S^ITA@T, ^TO PROIZWODNAQ NULEWOGO PORQDKA RAWNA SAMOJ FUNKCII.

dOKAZATELXSTWO. dLQ SOKRA]ENIQ ZAPISI NE BUDEM PISATX ARGU- MENTY U PROIZWODNYH.

dOKAVEM FORMULU lEJBNICA PO INDUKCII. pRI n = 1 FORMULA (5.5.2) IMEET WID

1

(u v)0 = X C1k u(k) v(1;k) = u v0 + u0 v

k=0

T.E. \TO FORMULA DLQ PERWOJ PROIZWODNOJ PROIZWEDENIQ DWUH FUNK- CIJ.

pREDPOLOVIM TEPERX, ^TO RAWENSTWO (5.5.2) DOKAZANO DLQ POKA- ZATELQ n = m I USTANOWIM EGO SPRAWEDLIWOSTX PRI n = m + 1.

iMEEM

m

0

(u v)(m+1) = ((u v)(m))0

=

X

Ck u(k) v(m;k)

=

m

k=0

m

;m+1

m

;

m

X

0

X

= C

k

u

(k)

v

(m;k)

= C

k

u

(k+1)

v

(m;k)

+ u

(k)

v

(m+1;k)

=

m

m

k=0

X

k=0

X

=

Cmi;1u(i) v(m;(i;1))

+

Cmi u(i) v(m+1;i) =

i=1

i=0

m

=

X

(Cmi;1 + Cmi )u(i) v(m+1;i) + Cmmu(m+1) v(0) + Cm0 u(0) v(m+1):

i=1

nO SOGLASNO (5.5.1)

Ci;1 + Ci

=

m!

+

m!

=

m

m

(i ; 1)! (m ; (i ;

1))! i! (m

; i)!

=

m!

(i + m

;

i + 1) =

(m + 1)!

= Cmi +1:

i! (m ; i + 1)!

i!(m ; i + 1)!

kROME TOGO,

Cmm = 1 = Cmm+1+1

Cm0 = 1 = Cm0 +1:

pO\TOMU

m

(u v)(m+1) = Cm0 +1u(0) v(m+1) + XCmi +1u(i) v(m+1;i) + i=1

101

m+1

+Cmm+1+1u(m+1) v(0) = X Cmi +1u(i) v(m+1;i) i=0

I MY POLU^ILI FORMULU (5.5.2) DLQ n = m + 1. tEOREMA DOKAZANA.

rASSMOTRIM TEPERX DIFFERENCIALY WYS[IH PORQDKOW.

pUSTX x | NEZAWISIMAQ PEREMENNAQ I FUNKCIQ y = f(x) DIFFE- RENCIRUEMA. tOGDA dy = f0(x)dx I, ZNA^IT, DIFFERENCIAL dy ZAWI- SIT OT x I OT dx.

pOSTAWIM WOPROS, QWLQETSQ LI DIFFERENCIAL dy KAK FUNKCIQ OT x DIFFERENCIRUEMOJ FUNKCIEJ.

~TOBY WYQSNITX \TO, WNOWX PRIDADIM ARGUMENTU x PRIRA]ENIE dx I RASSMOTRIM PRIRA]ENIE DIFFERENCIALA dy

		;		00
f0(x + dx)dx ; f0	(x) dx =		f0	(x + dx) ; f0(x)		dx:	(5.5.3)

eSLI SU]ESTWUET WTORAQ PROIZWODNAQ f (x), TO RAZNOSTX (5.5.3) MOVNO PREDSTAWITX W WIDE

;

;

!

f0(x + dx) ; f0(x)

dx = f00(x)dx + o(dx)

dx =

00

2

;

2

2

= f

(x)(dx)

+ o (dx)

dx

0:

kWADRAT DIFFERENCIALA NEZAWISIMOJ PEREMENNOJ (dx)	PRINQTO
OBOZNA^ATX dx2. w TAKOJ ZAPISI dx S^ITAETSQ EDINYM SIMWOLOM,
KOTORYJ WOZWODITSQ W KWADRAT.
tAKIM OBRAZOM, POLAGAQ PO OPREDELENI@ d2y := d(dy), POLU^AEM
d2y = f00(x)dx2:	(5.5.4)

tAK KAK DIFFERENCIRUEMOSTX FUNKCII RAWNOSILXNA SU]ESTWOWANI@ PROIZWODNOJ, TO SU]ESTWOWANIE WTOROGO DIFFERENCIALA d2y RAWNOSILXNO SU]ESTWOWANI@ WTOROJ PROIZWODNOJ f00(x).

pOSKOLXKU DIFFERENCIAL NEZAWISIMOJ PEREMENNOJ dx OT x NE
ZAWISIT, TO d2x = d(dx) = 0.
dLQ n > 2 ANALOGI^NO POLAGAEM
dny := d(dn;1y)
I NAHODIM
dny = f(n)(x)dxn	(5.5.5)
GDE dxn OBOZNA^AET n-U@ STEPENX DIFFERENCIALA dx.

102

	oTS@DA SLEDUET, ^TO
	f(n)(x) =	dny	n = 1 2 : : : :	(5.5.6)
		dxn

nAPOMNIM, ^TO FORMULY (5.5.4) I (5.5.5) WYWEDENY W PREDPOLO- VENII, ^TO x QWLQETSQ NEZAWISIMOJ PEREMENNOJ.

rASSMOTRIM DIFFERENCIALY SLOVNOJ FUNKCII.

sNA^ALA NAJDEM WYRAVENIE DLQ DIFFERENCIALA PERWOGO PORQD-

KA SLOVNOJ FUNKCII. pUSTX ZADANA SLOVNAQ FUNKCIQ y = (x) =
'(f(x)), GDE FUNKCII y = '(u)	I u = f(x) IME@T PROIZWODNYE
PERWOGO PORQDKA. tOGDA dy =	0(x) dx I W SILU RAWENSTWA (5.4.1)
0(x) = '0(u)f0(x).
pO\TOMU
dy = '0(u)f0(x) dx:

s DRUGOJ STORONY, du = f0(x) dx I, ZNA^IT, dy = '0(u) du. tAKIM OBRAZOM, DLQ DIFFERENCIALA dy SPRAWEDLIWY FORMULY

dy = 0(x) dx	(5.5.7)
I
dy = '0(u) du:	(5.5.8)

|TI FORMULY WYGLQDQT ODINAKOWO, NO IH PRINCIPIALXNAQ RAZ- NICA SOSTOIT W TOM, ^TO W (5.5.7) dx QWLQETSQ DIFFERENCIALOM NE- ZAWISIMOJ PEREMENNOJ, A W (5.5.8) du QWLQETSQ DIFFERENCIALOM ZA- WISIMOJ PEREMENNOJ.

sWOJSTWO PERWOGO DIFFERENCIALA IMETX ODINAKOWOE WYRAVEN- NIE ^EREZ DIFFERENCIALY NEZAWISIMOJ I ZAWISIMOJ PEREMENOJ NA- ZYWA@T INWARIANTNOSTX@ FORMY PERWOGO DIFFERENCIALA.

dIFFERENCIALY WYS[IH PORQDKOW PODOBNOJ INWARIANTNOSTX@ NE OBLADA@T.

pUSTX PO-PREVNEMU y = '(u), u = f(x), GDE x | NEZAWISIMAQ PEREMENNAQ.

sOGLASNO (5.5.8) I (5.2.6)

d2y = d('0(u) du) = d('0(u)) du + '0(u) d(du) = = '00(u) du du + '0(u) d2u = '00(u) du2 + '0(u) d2u:

iTAK,
d2y = '00(u) du2 + '0(u) d2u:	(5.5.9)

103

zDESX d2u MOVET NE RAWNQTXSQ NUL@, TAK KAK u | ZAWISIMAQ PEREMENNAQ I d2 u = f00(x) dx2.

sRAWNENIE FORMUL (5.5.9) I (5.5.4) POKAZYWAET, ^TO WTOROJ DIF- FERENCIAL NE OBLADAET SWOJSTWOM INWARIANTNOSTI | EGO WYRAVE- NIE ZAWISIT OT TOGO, ZAPISYWAETSQ LI ON ^EREZ DIFFERENCIALY NE- ZAWISIMOJ PEREMENNOJ ILI ^EREZ DIFFERENCIALY ZAWISIMOJ PERE- MENNOJ.

nAJDEM E]E WYRAVENIE TRETXEGO DIFFERENCIALA FUNKCII ^EREZ DIFFERENCIALY ZAWISIMOJ PEREMENNOJ. iMEEM

d3y = d(d2y) = d('00(u) du2 + '0(u) d2u) =

='000(u) du3 + '00(u) d(du2) + '00(u) du d2u + '0(u) d(d2u) =

='000(u) du3 + 3'00(u) d2u du + '0(u) d3u:

(5.5.10)

fORMULY (5.5.9) I (5.5.10) ZAPOMINATX NE NUVNO. kAVDYJ RAZ, KOGDA ONI NUVNY, REKOMENDUETSQ WYWODITX IH ZANOWO.

rASSMOTRIM, NAKONEC, WOPROS O PROIZWODNYH FUNKCIJ, ZADANNYH PARAMETRI^ESKI. sNA^ALA POQSNIM, KAK PONIMAETSQ PARAMETRI^ES- KOE ZADANIE FUNKCIJ.

pUSTX W NEKOTOROJ OKRESTNOSTI TO^KI t0 ZADANY FUNKCII x = x(t) I y = y(t), PRI^EM FUNKCIQ x(t) STROGO MONOTONNA I NEPRERYWNA W \TOJ OKRESTNOSTI. tOGDA W OKRESTNOSTI TO^KI x0 := x(t0) SU]EST- WUET OBRATNAQ STROGO MONOTONNAQ NEPRERYWNAQ FUNKCIQ t = t(x). |TO POZWOLQET WWESTI SLOVNU@ FUNKCI@ y = y(t(x)), KOTORU@ I IME@T W WIDU, KOGDA GOWORQT O FUNKCII y = y(x), ZADANNOJ PARA- METRI^ESKI FORMULAMI x = x(t), y = y(t).

bUDEM TEPERX DOPOLNITELXNO S^ITATX, ^TO W TO^KE t0 SU]ESTWU-

@T PROIZWODNYE x0 , y0

I x0

(t

) = 0. pOKAVEM, ^TO W \TOM SLU^AE

t

t

t

0

60

W TO^KE x0, NE NAHODQ QWNO FUNK-

MOVNO WY^ISLITX PROIZWODNU@ yx

CI@ t = t(x).

iMEEM

yt0

0

0

0

yx

= yt tx = x0 :

t

eSLI FUNKCIQ y0

=x0

IMEET PROIZWODNU@ (TAK BUDET WO WSQKOM

t

t

SLU^AE, KOGDA SU]ESTWU@T WTORYE PROIZWODNYE xt00t(t) I yt00t(t)), TO

WTORU@ PROIZWODNU@ y00

MOVNO NAJTI PO FORMULE

xx

y0

0

y0

0

y0

0 1

00

0 0

t

t

0

t

yxx

= (yx)x = xt0 x

= xt0

t tx = xt0

t

xt0

:

pODOBNYM OBRAZOM MOVNO NAHODITX PROIZWODNYE FUNKCII y(x) BOLEE WYSOKOGO PORQDKA, ESLI ONI SU]ESTWU@T.

104

gLAWA 6

swojstwa differenciruemyh funkcij

x 6.1. wOZRASTANIE I UBYWANIE FUNKCII W TO^KE

nARQDU S WOZRASTANIEM I UBYWANIEM FUNKCIJ NA PROMEVUTKE RASSMATRIWAETSQ WOZRASTANIE I UBYWANIE FUNKCII W TO^KE. oPREDELENIE. pUSTX FUNKCIQ f(x) ZADANA W NEKOTOROJ OKRESTNOS-

TI TO^KI x0. gOWORQT, ^TO f STROGO WOZRASTAET W TO^KE x0, ESLI SU]ESTWUET TAKAQ OKRESTNOSTX TO^KI x0, ^TO DLQ x IZ \TOJ OKREST- NOSTI, LEVA]IH SLEWA OT x0, SPRAWEDLIWO NERAWENSTWO f(x) < f(x0), A DLQ x, LEVA]IH SPRAWA OT x0, | NERAWENSTWO f(x) > f(x0).

eSLI W \TIH NERAWENSTWAH ZNAKI < I > ZAMENENY SOOTWETSTWEN- NO NA 6 I >, TO GOWORQT, ^TO FUNKCIQ f WOZRASTAET (TO^NEE, NE UBYWAET) W TO^KE x0.

aNALOGI^NO OPREDELQ@TSQ STROGOE UBYWANIE I UBYWANIE FUNK- CII W TO^KE. mOVNO GOWORITX TAKVE OB ODNOSTORONNEM WOZRASTANII I UBYWANII W TO^KE.

oSNOWNYMI QWLQ@TSQ SLU^AI STROGOGO WOZRASTANIQ I UBYWANIQ FUNKCII W TO^KE, A NESTROGOE WOZRASTANIE I UBYWANIE RASSMATRI- WA@T REVE.

tEOREMA 6.1.1. pUSTX FUNKCIQ y = f(x) IMEET W TO^KE x0 PROIZWODNU@. tOGDA W TO^KE x0 FUNKCIQ f STROGO WOZRASTAET, ESLI f0(x0) > 0, I STROGO UBYWAET, ESLI f0(x0) < 0.

dOKAZATELXSTWO. pUSTX f0(x0) > 0. tAK KAK

f0(x0) = lim y

x!0 x

TO DLQ DOSTATO^NO MALYH x

xy > 0:

zNA^IT, ESLI x > 0, TO y = f(x0 + x) ; f(x) > 0, A ESLIx < 0, TO y < 0. a \TO OZNA^AET STROGOE WOZRASTANIE FUNKCII f

W TO^KE x0.

aNALOGI^NO RASSMATRIWAETSQ SLU^AJ, KOGDA f0(x0) < 0.

w TEOREME 6.1.1 MOVNO IMETX W WIDU ODNOSTORONNIE PROIZWODNYE, NO TOGDA W UTWERVDENII NUVNO GOWORITX OB ODNOSTORONNEM STROGOM WOZRASTANII ILI STROGOM UBYWANII FUNKCII.

105

oPREDELENIE. gOWORQT, ^TO FUNKCIQ f(x) IMEET W TO^KE x0 LOKALXNYJ MAKSIMUM, ESLI DLQ WSEH x IZ NEKOTOROJ OKRESTNOSTI TO^- KI x0 WYPOLNQETSQ NERAWENSTWO f(x) 6 f(x0). a ESLI DLQ WSEH x IZ NEKOTOROJ PROKOLOTOJ OKRESTNOSTI TO^KI x0 WYPOLNQETSQ NERAWEN- STWO f(x) < f(x0), TO GOWORQT, ^TO FUNKCIQ f(x) IMEET W TO^KE x0

STROGIJ LOKALXNYJ MAKSIMUM.

gOWORQT, ^TO FUNKCIQ f(x) IMEET W TO^KE x0 LOKALXNYJ MINIMUM, ESLI DLQ WSEH x IZ NEKOTOROJ OKRESTNOSTI TO^KI x0 WYPOLNQET- SQ NERAWENSTWO f(x) > f(x0). a ESLI DLQ WSEH x IZ NEKOTOROJ PROKO- LOTOJ OKRESTNOSTI TO^KI x0 WYPOLNQETSQ NERAWENSTWO f(x) > f(x0), TO GOWORQT, ^TO FUNKCIQ f(x) IMEET W TO^KE x0 STROGIJ LOKALXNYJ MINIMUM.

tO^KI LOKALXNOGO MAKSIMUMA I MINIMUMA FUNKCII NAZYWA@T TO^KAMI EE LOKALXNOGO \KSTREMUMA, A TO^KI STROGOGO LOKALXNOGO MAKSIMUMA I MINIMUMA | TO^KAMI STROGOGO LOKALXNOGO \KSTREMU- MA.

w \TIH OPREDELENIQH SLOWO \LOKALXNYJ" DOBAWLQ@T POTOMU, ^TO ^ISLO f(x0) SRAWNIWAETSQ SO ZNA^ENIQMI FUNKCII TOLXKO W DOSTA- TO^NO MALOJ OKRESTNOSTI TO^KI x0 W OTLI^IE OT \GLOBALXNOGO" MAK- SIMUMA I MINIMUMA, KOTORYE OTNOSQTSQ KO WSEJ OBLASTI ZADANIQ FUNKCII.

tEOREMA 6.1.2 (tEOREMA fERMA). eSLI FUNKCIQ f(x) IMEET W TO^KE x0 PROIZWODNU@, TO DLQ TOGO ^TOBY W TO^KE x0 FUNKCIQ

fIMELA LOKALXNYJ \KSTREMUM, NEOBHODIMO WYPOLNENIE RAWENSTWA

f0(x0) = 0.

dOKAZATELXSTWO. iZ NERAWENSTWA f0(x0) > 0 SLEDUET STROGOE WOZ- RASTANIE FUNKCII f W TO^KE x0, A IZ NERAWENSTWA f0(x0) < 0 | STROGOE UBYWANIE f W TO^KE x0. zNA^IT, LOKALXNYJ \KSTREMUM WOZ- MOVEN TOLXKO PRI USLOWII f0(x0) = 0.

uSLOWIE f0(x0) = 0, BUDU^I NEOBHODIMYM DLQ LOKALXNOGO \KS- TEMUMA, NE QWLQETSQ DOSTATO^NYM. dEJSTWITELXNO, FUNKCIQ y = x3 STROGO WOZRASTAET NA WSEJ OSI. wMESTE S TEM, EE PROIZWODNAQ y0 = 3x2 OBRA]AETSQ W NULX PRI x = 0.

tEOREMA 6.1.3 (tEOREMA dARBU O PROMEVUTO^NYH ZNA^ENI-

		0		6
QH).	pUSTX FUNKCIQ f(x)	ZADANA NA OTREZKE	[a b], f(a)	= f(b)

I SU]ESTWUET FUNKCIQ F (x) TAKAQ, ^TO F (x) = f(x) DLQ WSEH x 2 [a b]. tOGDA DLQ L@BOGO ^ISLA , ZAKL@^ENNOGO STROGO MEVDU f(a) I f(b), NAJDETSQ TO^KA 2 (a b) TAKAQ, ^TO f( ) = .

dOKAZATELXSTWO. sNA^ALA RASSMOTRIM SLU^AJ, KOGDA ^ISLA f(a) I f(b) IME@T RAZNYE ZNAKI I RAWNO NUL@.

pUSTX DLQ OPREDELENNOSTI f(a) > 0 I f(b) < 0.

106

fUNKCIQ F (x) NEPRERYWNA NA OTREZKE [a b] I, ZNA^IT, PRINIMA-

0	2
ET W NEKOTOROJ TO^KE		[a b] SWOE MAKSIMALXNOE ZNA^ENIE. tAK KAK

F (a) = f(a) > 0, TO W TO^KE a FUNKCIQ F STORGO WOZRASTAET, PO\TO- MU NE MOVET BYTX TO^KOJ a. tO^NO TAKVE NE MOVET RAWNQTXSQ b, TAK KAK IZ USLOWIQ F 0(b) = f(b) < 0 SLEDUET, ^TO F STROGO UBYWAET W TO^KE b.

sLEDOWATELXNO, | WNUTRENNQQ TO^KA OTREZKA [a b] I TOGDA PO TEOREME fERMA F 0( ) = 0. nO F 0( ) = f( ) I, TAKIM OBRAZOM, f( ) =

0.

eSLI WYPOLNQ@TSQ USLOWIQ f(a) < 0 I f(b) > 0, TO W KA^ESTWE MOVNO WZQTX TO^KU, W KOTOROJ F (x) PRINIMAET MINIMALXNOE ZNA^E- NIE NA OTREZKE [a b], I ANALOGI^NYM OBRAZOM DOKAZATX, ^TO f( ) = 0. tAKIM OBRAZOM, W RASSMATRIWAEMOM ^ASTNOM SLU^AE TEOREMA DO-

KAZANA.

pEREHOD K OB]EMU SLU^A@ OSU]ESTWLQETSQ TAK VE, KAK PRI DOKA- ZATELXSTWE TEOREMY kO[I 4.3.3 O PROMEVUTO^NYH ZNA^ENIQH. wWO- DIM FUNKCI@ '(x) := f(x) ; . tAK KAK ^ISLO ZAKL@^ENO STROGO MEVDU f(a) I f(b), TO FUNKCIQ '(x) PRINIMAET W TO^KAH a I b ZNA^E- NIQ RAZNYH ZNAKOW. kROME TOGO, ESLI POLOVITX (x) := F (x) ; x, TO 0(x) = (F(x) ; x)0 = '(x). pO\TOMU W SILU UVE DOKAZANNOGO ^ASTNOGO SLU^AQ TEOREMY SU]ESTWUET TAKAQ TO^KA 2 (a b), ^TO

'( ) = 0. oTS@DA f( ) ; = 0 I, ZNA^IT, f( ) = . tEOREMA DOKAZANA.

sRAWNIM TEOREMY dARBU I kO[I O PROMEVUTO^NYH ZNA^ENIQH. zAKL@^ENIE W OBEIH TEOREMAH ODINAKOWY, RAZNYMI QWLQ@TSQ USLO- WIQ NA FUNKCI@ f. w TEOREME kO[I TREBOWALASX NEPRERYWNOSTX

FUNKCII f(x), A W TEOREME dARBU PREDPOLAGAETSQ SU]ESTWOWANIE
FUNKCII F (x) TAKOJ, ^TO F0(x) = f(x) DLQ WSEH x 2 [a b].
nO PROIZWODNAQ MOVET SU]ESTWOWATX W KAVDOJ TO^KE I NE BYTX
NEPRERYWNOJ. |TO WIDNO NA PRIMERE FUNKCII
F (x) :=		x2 sin(1=x)			PRI x = 0,
		(0				6
					PRI x = 0,
DLQ KOTOROJ	(
F0(x) =	2x sin(1=x)		;	cos(1=x)		PRI x = 0,
	0					6
						PRI x = 0

I F 0(x) IMEET RAZRYW W TO^KE 0.

pO\TOMU TEOREMA dARBU NE SLEDUET IZ TEOREMY kO[I. nA SAMOM DELE TEOREMA kO[I QWLQETSQ SLEDSTWIEM TEOREMY dARBU, TAK KAK DLQ KAVDOJ NEPRERYWNOJ FUNKCII f SU]ESTWUET FUNKCIQ F TAKAQ, ^TO F0(x) = f(x) DLQ WSEH x 2 [a b]. |TO BUDET DOKAZANO W GLAWE 9.

107

x 6.2. tEOREMY O SREDNEM

w \TOM PARAGRAFE RASSMATRIWA@TSQ FUNKCII, NEPRERYWNYE NA OTREZKE [a b] I DIFFERENCIRUEMYE, T.E. IME@]IE PROIZWODNU@, NA INTERWALE (a b).

tEOREMA 6.2.1 (tEOREMA rOLLQ). pUSTX FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a b] I DIFFERENCIRUEMA NA INTERWALE (a b).

eSLI f(a) = f(b),	TO SU]ESTWUET TO^KA	2	(a b) TAKAQ, ^TO
f0( ) = 0.
dOKAZATELXSTWO.	tAK KAK FUNKCIQ f NEPRERYWNA NA OTREZKE [a b],

TO W NEKOTORYH TO^KAH ONA PRINIMAET SWOI MAKSIMALXNOE M I MI- NIMALXNOE m ZNA^ENIQ NA \TOM OTREZKE. eSLI M = m, TO f | IMEET \TO ZNA^ENIE WO WSEH TO^KAH IZ [a b] I PROIZWODNAQ f0(x) RAWNA NUL@ WS@DU NA (a b).

eSLI VE M 6= m, TO PO KRAJNEJ MERE ODNO IZ \TIH ZNA^ENIJ FUNKCIQ f PRINIMAET WO WNUTRENNEJ TO^KE OTREZKA [a b]. tOGDA PO TEOREME fERMA W \TOJ TO^KE PROIZWODNAQ f0 RAWNA NUL@ I TEOREMA DOKAZANA.

tEOREMA rOLLQ POKAZYWAET, ^TO W NEKOTOROJ TO^KE INTERWALA (a b) KASATELXNAQ K GRAFIKU FUNKCII PARALLELXNA OSI OX. tEOREMA 6.2.2 (tEOREMA lAGRANVA O SREDNEM). pUSTX FUNK-

CIQ f(x) NEPRERYWNA NA OTREZKE [a b] I DIFFERENCIRUEMA NA INTERWALE (a b). tOGDA SU]ESTWUET TO^KA 2 (a b) TAKAQ, ^TO

f(b) ; f(a) = f0( )(b ; a):

(6.2.1)

dOKAZATELXSTWO. sWEDEM ZADA^U K TEOREME rOLLQ. dLQ \TOGO WYBE- REM ^ISLO TAK, ^TOBY DLQ FUNKCII '(x) := f(x); x WYPOLNQLOSX RAWENSTWO '(a) = '(b). rE[IW URAWNENIE f(a) ; a = f(b) ; b, WI- DIM, ^TO \TO USLOWIE WYPOLNQETSQ PRI

= f(b) ; f(a) : b ; a

fUNKCIQ '(x) NEPRERYWNA NA [a b] I DIFFERENCIRUEMA NA (a b). pO TEOREME rOLLQ SU]ESTWUET TO^KA 2 (a b) TAKAQ, ^TO

'0( ) = 0:

|TO RAWENSTWO OZNA^AET, ^TO f0( ) ; = 0 I, TAKIM OBRAZOM,

f0( ) ; f(b) ; f(a) = 0: b ; a

tEOREMA DOKAZANA.

108

fORMULU (6.2.1) NAZYWA@T FORMULOJ KONE^NYH PRIRA]ENIJ lA-

GRANVA. oNA QWLQETSQ ODNIM IZ OSNOWNYH REZULXTATOW DIFFEREN- CIALXNOGO IS^ISLENIQ.

~TOBY WYQSNITX GEOMETRI^ESKIJ SMYSL FORMULY KONE^NYH PRI- RA]ENIJ lAGRANVA, ZAPI[EM EE W WIDE

f0( ) =	f(b) ; f(a)	:	(6.2.2)
	b ; a

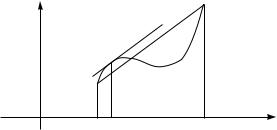
lEWAQ ^ASTX RAWENSTWA (6.2.2) RAWNA TANGENSU UGLA NAKLONA KASA- TELXNOJ K GRAFIKU FUNKCII f(x) W TO^KE , A PRAWAQ ^ASTX | TAN- GENSU UGLA NAKLONA PRQMOJ, SOEDINQ@]EJ TO^KI (a f(a)) I (b f(b)) GRAFIKA FUNKCII.

tAKIM OBRAZOM, TEOREMA lAGRANVA POKAZYWAET, ^TO SU]ESTWUET TO^KA 2 (a b), KASATELXNAQ W KOTOROJ PARALLELXNA PRQMOJ, SOEDI- NQ@]EJ TO^KI (a f(a)) I (b f(b)) GRAFIKA FUNKCII.

y

a ξ b x

dRUGAQ FORMA ZAPISI FORMULY KONE^NYH PRIRA]ENIJ lAGRANVA

TAKOWA:
f(b) ; f(a) = f0(a + (b ; a))(b ; a)	(6.2.3)

GDE | NEKOTOROE ^ISLO, UDOWLETWORQ@]EE USLOWI@ 0 < < 1.

w FORMULIROWKE TEOREMY 6.2.2 PREDPOLAGAETSQ, ^TO a < b. nO LEGKO WIDETX, ^TO FORMULA (6.2.1) IMEET MESTO I W TOM SLU^AE, KOGDA a > b.

tEOREMA 6.2.3 (tEOREMA kO[I O SREDNEM). pUSTX NA OTREZ-

KE [a b] ZADANY NEPRERYWNYE FUNKCII f(x) I g(x), PRI^EM g(a) =6 g(b). pREDPOLOVIM, ^TO f I g DIFFERENCIRUEMY NA INTERWALE (a b) I PROIZWODNYE f0(x) I g0(x) NE OBRA]A@TSQ NA (a b) W NULX ODNOWREMENNO. tOGDA SU]ESTWUET TO^KA 2 (a b) TAKAQ, ^TO

f(b) ; f(a)	=	f0( )	:	(6.2.4)
g(b) ; g(a)		g0( )

109

dOKAZATELXSTWO. dLQ g(x) = x TEOREMA 6.2.3 SOWPADAET S TEOREMOJ 6.2.2. dOKAZATELXSTWO TEOREMY 6.2.3 BUDET IDTI PO TOJ VE SHEME.

wWEDEM FUNKCI@ '(x) := f(x) ; g(x). oNA NEPRERYWNA NA [a b] I DIFFERENCIRUEMA NA (a b). ~TOBY K FUNKCII '(x) MOVNO BYLO PRIMENITX TEOREMU rOLLQ, SOSTAWIM URAWNENIE f(b); g(b) = f(a);g(a), RE[IW KOTOROE, POLU^IM

= f(b) ; f(a) : g(b) ; g(a)

dLQ \TOGO IMEEM '(a) = '(b). pO\TOMU SU]ESTWUET TO^KA				2
(a b), DLQ KOTOROJ '0( ) = 0. oTS@DA
f(b)	f(a)	g0( ) = 0:
f0( ) ; g(b)	; g(a)		(6.2.5)
	;

pRI \TOM g0( ) 6= 0, TAK KAK INA^E IZ (6.2.5) SLEDOWALO BY, ^TO I f0( ) = 0, A PROIZWODNYE FUNKCIJ f I g NE MOGUT OBRA]ATXSQ W NULX ODNOWREMENNO.

tAKIM OBRAZOM, LEWU@ I PRAWU@ ^ASTI RAWENSTWA (6.2.5) MOVNO RAZDELITX NA g0( ), ^TO PRIWODIT K (6.2.4).

tEOREMA DOKAZANA.

pOLU^IM NEKOTORYE SLEDSTWIQ IZ TEOREMY lAGRANVA O SREDNEM.

tEOREMA 6.2.4. pUSTX FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a b] I f0(x) = 0 WO WSEH TO^KAH INTERWALA (a b). tOGDA FUNKCIQ f POSTOQNNA NA OTREZKE [a b].

dOKAZATELXSTWO. dLQ L@BOJ PARY TO^EK x I x IZ OTREZKA [a b] PO FORMULE KONE^NYH PRIRA]ENIJ lAGRANVA SU]ESTWUET TAKAQ TO^- KA 2 (x x ), RASPOLOVENNAQ MEVDU x I x , ^TO

f(x ) ; f(x ) = f0( )(x ; x ):

nO TAK KAK PRINADLEVIT INTERWALU (a b), TO f0( ) = 0 I, ZNA^IT, f(x ) = f(x ). tEOREMA DOKAZANA, TAK KAK TO^KI x I x BYLI PROIZWOLXNYMI TO^KAMI OTREZKA [a b].

pOKAVEM, ^TO USLOWIQ \TOJ TEOREMY MOVNO NESKOLXKO OSLABITX.

tEOREMA 6.2.5. pUSTX FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a b] I f0(x) = 0 WO WSEH TO^KAH INTERWALA (a b) ZA ISKL@^ENIEM KONE^NOGO ^ISLA TO^EK, W KOTORYH SU]ESTWOWANIE PROIZWODNOJ NE PREDPOLAGAETSQ. tOGDA FUNKCIQ f POSTOQNNA NA OTREZKE [a b].

dOKAZATELXSTWO. pUSTX a = x0 < x1 < < xn = b | TE TO^KI, IZ OTREZKA [a b], W KOTORYH PROIZWODNAQ f0(x) MOVET NE SU]ESTWOWATX.

110