Матан, Лекции - Теляковский 1

y	y=f –1(x)			y=x
	( f(x),x)			y=f(x)
				(x,f(x))

f(x) x x

x 4.6. pOKAZATELXNAQ FUNKCIQ

nA^NEM S OPREDELENIQ STEPENI ax PRI IRRACIONALXNYH ZNA^ENI- QH POKAZATELQ x.

bUDEM S^ITATX, ^TO ^ISLO a UDOWLETWORQET ESTESTWENNYM USLO- WIQM a > 0 I a 6= 1, NE OTME^AQ \TO.

rASSMOTRIM SNA^ALA STEPENX ax DLQ RACIONALXNYH ZNA^ENIJ PO- KAZATELQ x. pRI \TOM MNOGOE BUDET POWTORQTX RASSUVDENIQ, PROWO- DIW[IESQ W [KOLXNOM KURSE.

pO OPREDELENI@ STEPENNOJ FUNKCII a1 := a I PRI NATURALXNYH

n > 2

an := a a a :

pUSTX TEPERX ^ISLO x IMEET| WID{zn1=n,}GDE n 2 N.

pRI FIKSIROWANNOM NATURALXNOM n RASSMOTRIM FUNKCI@ u = vn v 2 [0 1). |TA FUNKCIQ STROGO WOZRASTAET I NEPRERYWNA, OB- LASTX EE ZNA^ENIJ [0 1). zNA^IT, SOGLASNO TEOREMAM PREDYDU]EGO

PARAGRAFA OBRATNAQ FUNKCIQ v = pn u = u1=n OPREDELENA NA POLUOSI [0 1) I NEPRERYWNA NA NEJ.

w [KOLXNOM KURSE SU]ESTWOWANIE ARIFMETI^ESKOGO KORNQ n-OJ STEPENI IZ POLOVITELXNOGO ^ISLA S^ITALOSX SAMO SOBOJ RAZUME@- ]IMSQ. tEPERX \TOT FAKT POLU^IL OBOSNOWANIE.

iTAK, STEPENX ax OPREDELENA DLQ ^ISEL x WIDA 1=n. eSLI x = p=q, GDE p I q { NATURALXNYE ^ISLA, TO PO OPREDELENI@ POLAGA@T

ap=q := (ap)1=q:

zDESX MOVNO BYLO BY BRATX I (a1=q)p, NO RAWENSTWO (ap)1=q = (a1=q)p NUVDAETSQ W DOKAZATELXSTWE.

eSLI x = 0, TO a0 := 1, A ESLI x = ;p=q, GDE p I q | NATURALXNYE ^ISLA, TO PO OPREDELENI@ a;p=q := 1=ap=q.

71

tAKIM OBRAZOM, STEPENX ax OPREDELENA DLQ WSEH RACIONALXNYH x. pRI \TOM WYPOLNQ@TSQ SLEDU@]IE SWOJSTWA (BUKWY r OBOZNA^A@T PROIZWOLXNYE RACIONALXNYE ^ISLA):

ar > 0

ar1+r2 = ar1 ar2

(ar1 )r2 = ar1 r2

(ab)r = ar br a > 0 b > 0

ESLI a > 1, TO ar STROGO WOZRASTAET NA MNOVESTWE RACIONALXNYH
^ISEL (W ^ASTNOSTI, ESLI a > 1 I r > 0, TO ar > 1) I	lim ar = +	1	,
	r!+1

lim ar = 0

r!;1

ESLI a < 1, TO ar STROGO UBYWAET NA MNOVESTWE RACIONALXNYH ^ISEL.

mY NE PRIWODIM OBOSNOWANIE \TIH SWOJSTW, TAK KAK ONO AKKU- RATNO PROWEDENO W [KOLXNOM KURSE, GDE NE BYLO DOKAZANO TOLXKO SU]ESTWOWANIE ARIFMETI^ESKOGO KORNQ n-OJ STEPENI.

w DALXNEJ[IM PONADOBITSQ SLEDU@]EE UTWERVDENIE O STEPENQH S RACIONALXNYMI POKAZATELQMI.

lEMMA 4.6.1 (nERAWENSTWO bERNULLI). eSLI a > 1 I h 2

(0 1] | RACIONALXNOE ^ISLO, TO

0 < ah ; 1 6 2(a ; 1)h:

(4.6.1)

dOKAZATELXSTWO. pUSTX SNA^ALA h = 1=n, GDE n | NATURALXNOE

^ISLO. tOGDA a1=n = 1 + , GDE W SILU STROGOGO WOZRASTANIQ ax NA MNOVESTWE RACIONALXNYH ^ISEL > 0. pO\TOMU IZ NERAWENSTWA bERNULLI (2.6.1) WYTEKAET, ^TO

a = (1 + )n > 1 + n:

zNA^IT,

= ah ; 1 6 a ;n 1 = (a ; 1)h

T.E.

0 < ah ; 1 6 (a ; 1)h

I MY POLU^ILI NERAWENSTWO (4.6.1) DLQ RASSMATRIWAEMYH ZNA^ENIJ h DAVE BEZ MNOVITELQ 2 W PRAWOJ ^ASTI.

pUSTX TEPERX h | PROIZWOLXNOE RACIONALXNOE ^ISLO IZ (0 1). nAHODIM NATURALXNOE n TAKOE, ^TO 1=(n + 1) < h 6 1=n. tOGDA,

72

POLXZUQSX DOKAZANNYM UVE DLQ POKAZATELQ 1=n NERAWENSTWOM (4.6.1),

POLU^AEM

ah

;

1 6 a1=n

;

1 6 a ; 1

= n + 1

a ; 1

< n + 1 (a

;

1)h 6 2(a

;

1)h:

n

n

n + 1

n

lEMMA DOKAZANA.

bUDEM PO-PREVNEMU S^ITATX a > 1. dLQ RACIONALXNYH x IMEEM

ax =

sup ar:

(4.6.2)

r6x r2Q

pRIMEM FORMULU (4.6.2) W KA^ESTWE OPREDELENIQ ax PRI a > 1

DLQ IRRACIONALXNYH x. tEPERX STEPENX ax PRI a > 1 OPREDELENA

DLQ WSEH DEJSTWITELXNYH x.

nA[A CELX | WYQSNITX SWOJSTWA POKAZATELXNOJ FUNKCII y = ax,

W ^ASTNOSTI, DOKAZATX EE NEPRERYWNOSTX.

pERE^ISLIM SWOJSTWA FUNKCII ax PRI a > 1.

1 . ax > 0. |TO | PROSTOE SLEDSTWIE IZ (4.6.2).

2 . fUNKCIQ ax STROGO WOZRASTAET, T.E. ESLI x1 < x2, TO ax1

< ax2 .

sNA^ALA ZAMETIM, ^TO NESTROGOE NERAWENSTWO ax1 6 ax2

WYTE-

KAET IZ TOGO, ^TO DLQ ax2 W (4.6.2) WERHNQQ GRANX BERETSQ PO BOLEE [IROKOMU MNOVESTWU RACIONALXNYH ^ISEL, ^EM DLQ ax1 .

wOZXMEM RACIONALXNYE ^ISLA I TAKIE, ^TO x1 < < < x2. tOGDA W SILU STROGOJ MONOTONNOSTI ax DLQ RACIONALXNYH POKAZA-

TELEJ IMEEM

ax1 6 a < a 6 ax2

I MY POLU^ILI NUVNOE NERAWENSTWO.

3 . ax ! +1 PRI x ! +1 ax ! 0 PRI x ! ;1. -

|TO WYTEKAET IZ SWOJSTW STEPENI S CELYM POKAZATELEM I STRO GOGO WOZRASTANIQ FUNKCII ax.

4 . fUNKCIQ ax NEPRERYWNA.

zAFIKSIRUEM PROIZWOLXNU@ TO^KU x0 I DOKAVEM NEPRERYWNOSTX FUNKCII ax W \TOJ TO^KE.

sNA^ALA USTANOWIM NEPRERYWNOSTX SPRAWA. pUSTX x > x0 I x ; x0 < 1=2. wOZXMEM RACIONALXNYE ^ISLA I TAKIE, ^TO < x0 <

x < I ; < 2(x ; x0). tOGDA ; < 1 I POLXZUQSX SNA^ALA STROGIM WOZRASTANIEM FUNKCII ax, A ZATEM OCENKOJ (4.6.1), NAHODIM

ax ; ax0 < a ; a = a (a ; ; 1) <

< ax0 2(a ; 1)( ; ) < 4ax0 (a ; 1)(x ; x0):

tAK KAK MNOVITELX 4ax0 (a ; 1) OT x NE ZAWISIT, TO POLU^ENNAQ OCENKA DOKAZYWAET NEPRERYWNOSTX FUNKCII ax W TO^KE x0 SPRAWA.

73

pRI DOKAZATELXSTWE NEPRERYWNOSTI SLEWA RASSUVDENIQ ANALO- GI^NY. eSLI x < x0 I x0 ; x < 1=2, TO WYBIRAEM RACIONALXNYE

^ISLA I TAKIE, ^TO < x < x0 < I ; < 2(x0 ; x). tOGDA SPRAWEDLIWY OCENKI

ax0 ; ax < a ; a = a (a ; ; 1) <

< ax0 2(a ; 1)( ; ) < 4ax0 (a ; 1)(x ; x0)

POKAZYWA@]IE NEPRERYWNOSTX SLEWA.

5 . oSNOWNOE SWOJSTWO STEPENI: ax+y = ax + ay DLQ L@BYH x I y. wYBEREM TAKIE POSLEDOWATELXNOSTI RACIONALXNYH ^ISEL f ng I

f ng, ^TO n ! x I n ! y PRI n ! 1. tOGDA n + n ! x + y I W SILU OSNOWNOGO SWOJSTWA STEPENI DLQ RACIONALXNYH POKAZATELEJ

a n+ n = a n a n:

pEREHODIM W \TOM RAWENSTWE K PREDELU PRI n ! 1 I, POLXZUQSX NEPRERYWNOSTX@ POKAZATELXNOJ FUNKCII, POLU^AEM NUVNOE RAWEN- STWO.

pREVDE ^EM GOWORITX O DRUGIH SWOJSTWAH POKAZATELXNOJ FUNK- CII PRI a > 1, RASPROSTRANIM EE OPREDELENIE NA a < 1. eSLI 0 < a < 1, TO 1=a > 1 I POLOVIM

ax := 1 x : (1=a)

tOGDA WSE SWOJSTWA 1 {5 POKAZATELXNOJ FUNKCII PERENOSQTSQ NA SLU^AJ 0 < a < 1, NO TOLXKO TEPERX FUNKCIQ ax STROGO UBYWAET. pRODOLVAEM WYQSNENIE SWOJSTW POKAZATELXNOJ FUNKCII ax. tE- PERX OSNOWANIE STEPENI a | L@BOE POLOVITELXNOE ^ISLO, NE RAW-

NOE 1.

6 . dLQ PROIZWOLXNYH ^ISEL x I y

(ax)y = axy:

eSLI y | NATURALXNOE ^ISLO, TO IZ OSNOWNOGO SWOJSTWA STEPENI

POLU^AEM

(ax)y = ax ax ax = axy:

oTS@DA NAHODIM, ^TO ESLI q | NATURALXNOE ^ISLO, TO

| {zy }

(ax=q)q = a(x=q)q = ax

I, IZWLEKAQ KORENX STEPENI q, WIDIM, ^TO ax=q = (ax)1=q, T.E. SWOJSTWO 6 DOKAZANO DLQ ^ISEL y WIDA 1=q.

74

pUSTX TEPERX y = p=q, GDE p I q | NATURALXNYE ^ISLA. tOGDA W SILU UVE DOKAZANNOGO IMEEM

(ax)p=q = (ax)p (1=q) = (axp)1=q = ax (p=q)

A ESLI y = ;p=q, GDE p I q | NATURALXNYE ^ISLA, TO

(ax);p=q =	1		=		1	= a;x (p=q)
	x	p=q		a	x (p=q)
	(a )

I, ZNA^IT, SWOJSTWO 6 DOKAZANO DLQ RACIONALXNYH y.

tEPERX, ESLI y IRRACIONALXNO, WYBIRAEM POSLEDOWATELXNOSTX RACIONALXNYH ^ISEL n, SHODQ]U@SQ K y. tOGDA PO UVE DOKAZAN-

NOMU

(ax) n = ax n

I, POLXZUQSX NEPRERYWNOSTX@ POKAZATELXNOJ FUNKCII, PEREHODIM W \TOM RAWENSTWE K PREDELU PRI n ! 1. tAK POLU^AEM SWOJSTWO 60: W POLNOM OB_EME.

70: (ab)x = ax bx DLQ L@BYH POLOVITELXNYH a I b I L@BOGO x. dLQ DOKAZATELXSTWA DOSTATO^NO WZQTX POSLEDOWATELXNOSTX RA-

CIONALXNYH ^ISEL f ng, SHODQ]U@SQ K x, I PEREJTI K PREDELU W RAWENSTWE (ab) n = a n b n .

pODWEDEM ITOG. sTEPENX ax, a > 0, OPREDELENA DLQ WSEH x 2 R

I POKAZATELXNAQ FUNKCIQ ax OBLADAET WSEMI SWOJSTWAMI, KOTORYE

BYLI IZWESTNY IZ [KOLXNOGO KURSA DLQ RACIONALXNYH x. kROME
TOGO, POKAZATELXNAQ FUNKCIQ NEPRERYWNA NA WSEJ OSI.
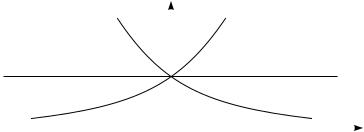
	nA RISUNKE IZOBRAVENY GRAFIKI FUNKCII ax PRI a > 1, a < 1,
A TAKVE PRI a = 1, KOTORYJ PRIWEDEN DLQ POLNOTY KARTINY.
		y
		a>1
1		a=1
		a<1
		O	x

x 4.7. |LEMENTARNYE FUNKCII

lOGARIFMI^ESKAQ FUNKCIQ. tAK KAK FUNKCIQ y = ax, GDE a > 0

I a =6 1, STROGO MONOTONNA I NEPRERYWNA NA WSEJ OSI, A OBLASTX

75

EE ZNA^ENIJ | POLUOSX (0 +1), TO NA (0 +1) MOVNO OPREDELITX OBRATNU@ FUNKCI@, KOTORU@ NAZYWA@T LOGARIFMI^ESKOJ FUNKCIEJ PO OSNOWANI@ a I OBOZNA^A@T x = loga y.

wYQSNIM SWOJSTWA LOGARIFMI^ESKOJ FUNKCII, PRI^EM NEZAWISI- MU@ PEREMENNU@, BUDEM, KAK OBY^NO, OBOZNA^ATX x, A ZAWISIMU@ y, T.E. BUDEM GOWORITX O FUNKCII y = loga x.

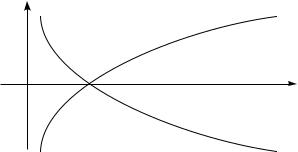
u^ITYWAQ HARAKTER MONOTONNOSTI FUNKCII ax, WIDIM, ^TO FUNK- CIQ loga x PRI a > 1 STROGO WOZRASTAET OT ;1 DO +1, A PRI 0 < a < 1 STROGO UBYWAET OT +1 DO ;1. gRAFIK LOGARIFMI^ESKOJ FUNKCII IMEET WID:

y

a>1

O	1	x
		0<a<1

iZ TOGO, ^TO POKAZATELXNAQ I LOGARIFMI^ESKAQ FUNKCII QWLQ- @TSQ WZAIMNO OBRATNYMI, WYTEKA@T TOVDESTWA

aloga x = x loga ax = x:

dOKAVEM SWOJSTWA LOGARIFMOW.

1 . loga(xy) = loga x + loga y DLQ L@BYH POLOVITELXNYH x I y.

iMEEM

aloga(xy) = xy = aloga xaloga y = aloga x+loga y :

tAK KAK POKAZATELXNAQ FUNKCIQ PRINIMAET KAVDOE SWOE ZNA^ENIE TOLXKO ODIN RAZ, TO W POLU^ENNOM RAWENSTWE MOVNO PRIRAWNQTX PO- KAZATELI STEPENI, ^TO PRIWODIT K TREBUEMOMU REZULXTATU.

2 . eSLI W FORMULE IZ 1 WMESTO x ZAPISATX x=y, TO POLU^IM loga xy y = loga x = loga xy + loga y

OTKUDA SLEDUET, ^TO DLQ PROIZWOLXNYH POLOVITELXNYH x I y loga xy = loga x ; loga y:

3 . eSLI x > 0, TO DLQ PROIZWOLXNOGO y SPRAWEDLIWO RAWENSTWO loga xy = y loga x:

76

w SAMOM DELE,

aloga xy = xy = aloga x y = ay loga x

I NUVNOE RAWENSTWO POLU^AEM, PRIRAWNIWAQ POKAZATELI STEPENI. 4 . eSLI ^ISLA a I b POLOVITELXNY I NE RAWNY 1, TO

loga b logb a = 1:

dEJSTWITELXNO,

aloga b logb a = aloga b	logb a = blogb a = a
I OPQTX PRIRAWNIWAEM POKAZATELI.

eSLI W KA^ESTWE OSNOWANIQ LOGARIFMA WZQTO ^ISLO e, TO TAKIE LOGARIFMY NAZYWA@T NATURALXNYMI. w SWQZI S \TIM ^ISLO e NA- ZYWA@T OSNOWANIEM NATURALXNYH LOGARIFMOW. dLQ NATURALXNOGO LOGARIFMA ^ISLA x ISPOLXZU@TSQ OBOZNA^ENIQ ln x I log x.

sTEPENNAQ FUNKCIQ. fUNKCI@ y = xa, GDE x > 0 I a | PROIZ-

WOLXNOE ^ISLO, NAZYWA@T STEPENNOJ FUNKCIEJ.

sTEPENNU@ FUNKCI@ MOVNO PREDSTAWITX KAK SLOVNU@ FUNKCI@

xa = eln x a = ea ln x:

oTS@DA W SILU TEOREMY O NEPRERYWNOSTI SLOVNOJ FUNKCII WYTEKA- ET NEPRERYWNOSTX STEPENNOJ FUNKCII, TAK KAK NEPRERYWNOSTX LO- GARIFMI^ESKOJ I POKAZATELXNOJ FUNKCIJ IZWESTNY.

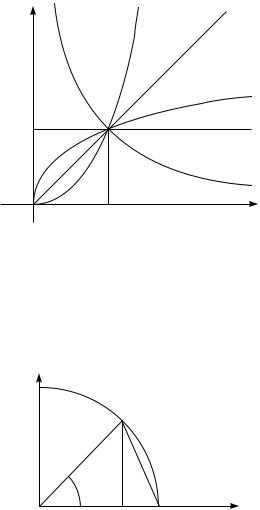
pRI a > 0 STEPENNU@ FUNKCI@ DOOPREDELQ@T W NULE, POLAGAQ 0a := 0. tOGDA FUNKCIQ y = xa STANOWITSQ NEPRERYWNOJ NA [0 +1). nA RISUNKE IZOBRAVENY GRAFIKI STEPENNOJ FUNKCII PRI RAZ-

LI^NYH ZNA^ENIQH POKAZATELQ a.

eSLI a | CELOE ^ISLO, TO FUNKCI@ xa MOVNO RASSMATRIWATX I DLQ OTRICATELXNYH ZNA^ENIJ x. pRI \TOM POLAGA@T x0 1 PRI WSEH x, W TOM ^ISLE I PRI x = 0. dLQ CELYH ZNA^ENIJ POKAZATELQ a STEPENNAQ FUNKCIQ QWLQETSQ ^ETNOJ ILI NE^ETNOJ W ZAWISIMOSTI OT ^ETNOSTI ILI NE^ETNOSTI a.

eSLI a | NE^ETNOE ^ISLO, TO FUNKCIQ xa OBRATIMA DLQ WSEH x PRI POLOVITELXNYH a I OBRATIMA DLQ WSEH x 6= 0 PRI OTRICATELX- NYH a.

tRIGONOMETRI^ESKIE FUNKCII. oPREDELENIE TRIGONOMETRI^ES- KIH FUNKCIJ IZWESTNO IZ [KOLXNOGO KURSA. dOKAVEM IH NEPRERYW- NOSTX.

77

y		a>1
		a=1
		0<a<1
1
		a=0
		a<0
O	1	x

tEOREMA 4.7.1. dLQ L@BOGO ZNA^ENIQ x SPRAWEDLIWO NERAWENSTWO

jsin xj 6 jxj:

(4.7.1)

dOKAZATELXSTWO. pRI x = 0 I LEWAQ I PRAWAQ ^ASTI NERAWENST-

WA (4.7.1) RAWNY NUL@. pOKAVEM, ^TO DLQ OSTALXNYH ZNA^ENIJ x W (4.7.1) IMEET MESTO STROGOE NERAWENSTWO. bUDEM S^ITATX, ^TO 0 < x < =2. rASSMOTRIM OKRUVNOSTX RADIUSA 1.

y

B

	x	A	x
O	C

wOZXMEM UGOL \AOB, RADIANNAQ MERA KOTOROGO RAWNA x. tOGDA DLINA DUGI ^ AB RAWNA x, A sin x = BC. nO DLINA DUGI ^ AB BOLX[E, ^EM DLINA HORDY AB, A DLINA OTREZKA AB KAK GIPOTENUZY PRQMOUGOLXNOGO TREUGOLXNIKA 4ABC BOLX[E, ^EM DLINA KATETA BC. |TIM NERAWENSTWO (4.7.1) DOKAZANO DLQ 0 < x < =2.

tAK KAK FUNKCII I W LEWOJ I W PRAWOJ ^ASTQH NERAWENSTWA (4.7.1) ^ETNYE, TO NERAWENSTWO (4.7.1) SPRAWEDLIWO I DLQ ; =2 < x < 0. a ESLI jxj > =2, TO (4.7.1) SLEDUET IZ TOGO, ^TO jsin xj 6 1.

tEOREMA DOKAZANA.

78

tEOREMA 4.7.2. kAVDAQ IZ FUNKCIJ y = sin x, y = cos x, y = tg x I y = ctg x NEPRERYWNA W SWOEJ OBLASTI OPREDELENIQ.

dOKAZATELXSTWO. nA^NEM S DOKAZATELXSTWA NEPRERYWNOSTI FUNK- CII y = sin x. dADIM ARGUMENTU PRIRA]ENIE x I RASSMOTRIM PRI- RA]ENIE FUNKCII:

y = sin(x + x) ; sin x = 2 cos x + 2x sin 2x : zNA^IT, W SILU (4.7.1)

j yj 6 2 sin 2x 6 j xj:

oTS@DA SLEDUET, ^TO y ! 0 PRI x ! 0, ^TO I DOKAZYWAET NEPRE- RYWNOSTX SINUSA.

nEPRERYWNOSTX KOSINUSA MOVNO DOKAZATX ANALOGI^NO, A MOVNO WOSPOLXZOWATXSQ RAWENSTWOM cos x = sin(x + =2) I TEOREMOJ O NE- PRERYWNOSTI SLOVNOJ FUNKCII.

nEPRERYWNOSTX TANGENSA I KOTANGENSA POLU^AEM, SSYLAQSX NA TEOREMU O NEPRERYWNOSTI ^ASTNOGO.

iZ NEPRERYWNOSTI FUNKCII TANGENS NA INTERWALE (; =2 =2) W SILU TEOREMY 4.5.2 SLEDUET, ^TO ZNA^ENIQMI \TOJ FUNKCII QWLQ- @TSQ WSE DEJSTWITELXNYE ^ISLA. tAK KAK FUNKCIQ TANGENS STROGO

WOZRASTAET NA (; =2 =2), TO ONA OSU]ESTWLQET WZAIMNO ODNOZNA^-
NOE SOOTWETSTWIE INTERWALOW (; =2 =2) I (;1 +1).
	w x1.8 BYLO USTANOWLENO, ^TO L@BOJ KONE^NYJ INTERWAL IMEET
MO]NOSTX KONTINUUM. pO\TOMU TEPERX MY MOVEM SKAZATX, ^TO I
MNOVESTWO WSEH DEJSTWITELXNYH ^ISEL IMEET MO]NOSTX KONTINUUM
(BEZ DOKAZATELXSTWA \TOT FAKT BYL PRIWEDEN W x1.8).
	y			y
			y= sh x			y=cth x
y=ch x					1
		1				y= th x
		x				x
					–1
				y= cth x

79

sinxx :

gIPERBOLI^ESKIE FUNKCII. fUNKCII

sh x :=	ex ; e;x		ch x :=	ex + e;x		th x :=	sh x		cth x :=	ch x
	2			2			ch x			sh x

NAZYWA@TSQ SOOTWETSTWENNO GIPERBOLI^ESKIM SINUSOM, GIPERBOLI- ^ESKIM KOSINUSOM, GIPERBOLI^ESKIM TANGENSOM I GIPERBOLI^ESKIM KOTANGENSOM.

oNI OPREDELENY DLQ WSEH x. iSKL@^ENIE SOSTAWLQET TOLXKO GI- PERBOLI^ESKIJ KOTANGENS, KOTORYJ NE OPREDELEN W TO^KE x = 0. wSE GIPERBOLI^ESKIE FUNKCII NEPRERYWNY W OBLASTI SWOEGO OPREDELE- NIQ. |TO WYTEKAET IZ TEOREMY O NEPRERYWNOSTI SLOVNOJ FUNKCII. oPREDELENIE. |LEMENTARNYMI FUNKCIQMI NAZYWA@TSQ POKAZA-

TELXNAQ, LOGARIFMI^ESKAQ, STEPENNAQ, OSNOWNYE I OBRATNYE TRIGO- NOMETRI^ESKIE FUNKCII I WSE FUNKCII, KOTORYE MOGUT BYTX POLU- ^ENY IZ PERE^ISLENNYH FUNKCIJ S POMO]X@ ARIFMETI^ESKIH DEJ- STWIJ, WZQTIQ OBRATNYH FUNKCIJ I POSTROENIQ SLOVNYH FUNKCIJ.

w SILU DOKAZANNYH TEOREM KAVDAQ \LEMENTARNAQ FUNKCIQ NEPRE- RYWNA W SWOEJ OBLASTI OPREDELENIQ.

x 4.8. wY^ISLENIE NEKOTORYH PREDELOW

w \TOM PARAGRAFE BUDUT NAJDENY PREDELY NEKOTORYH WYRAVE- NIJ WIDA

lim	f(x)		(4.8.1)
x!0	g(x)

KOGDA PREDEL FUNKCII g(x) PRI x ! 0 RAWEN NUL@ I PO\TOMU NELXZQ PEREHODITX K PREDELU OTDELXNO W ^ISLITELE I W ZNAMENATELE DROBI.

1 . nAJDEM PREDEL

lim

x!0

bUDEM OPIRATXSQ NA GEOMETRI^ESKIE SOOBRAVENIQ. pUSTX SNA^A- LA 0 < x < =2. rASSMOTRIM ^ASTX OKRUVNOSTI RADIUSA R S CENTROM W NA^ALE KOORDINAT, RASPOLOVENNU@ W PERWOM KWADRANTE.

iZ PODOBIQ PRQMOUGOLXNYH TREUGOLXNIKOW OAD I OCB NAHODIM

	AD		=	R
	R sin x			R cos x

T.E. AD = R tg x. zNA^IT, PLO]ADX TREUGOLXNIKA OAD RAWNA

12 R2 tg x:

80