Матан, Лекции - Теляковский 1

NY. zNA^IT, PO TEOREME 2.2.4

tEOREMA 3.3.3. eSLI DLQ FUNKCIJ f I g SU]ESTWU@T PREDELY

lim f(x) I	lim g(x) I W NEKOTOROJ PROKOLOTOJ OKRESTNOSTI
x!x0	x!x0
TO^KI x0 WYPOLNQETSQ NERAWENSTWO f(x) 6 g(x), TO
	lim f(x) 6 lim g(x):
	x!x0	x!x0

dOKAZATELXSTWO. sU]ESTWUET TAKAQ PROKOLOTAQ OKRESTNOSTX TO^- KI x0, W KOTOROJ OPREDELENY OBE FUNKCII f I g. wOZXMEM PROIZWOLX- NU@ POSLEDOWATELXNOSTX TO^EK fxng, PRINADLEVA]IH \TOJ PROKOLO- TOJ OKRESTNOSTI I SHODQ]IHSQ K x0.

tAK KAK xn ! x0, TO WSE ^LENY POSLEDOWATELXNOSTI fxng, NA^I- NAQ S NEKOTOROGO NOMERA n, POPADUT W TU OKRESTNOSTX TO^KI x0, W KOTOROJ f(x) 6 g(x), T.E. f(xn) 6 g(xn) DLQ WSEH DOSTATO^NO BOLX- [IH n. pO TEOREME 2.2.3 O PREDELAH POSLEDOWATELXNOSTEJ OTS@DA WYTEKAET, ^TO

lim f(xn)	6 lim g(xn)
n!1	n!1
I OSTALOSX TOLXKO ZAMETITX, ^TO IZ OPREDELENIQ PREDELA FUNKCII PO
gEJNE SLEDUET, ^TO lim f(xn) =	lim f(x) I lim g(xn) =		lim g(x).
n!1	x!x0	n!1	x!x0

tEOREMA DOKAZANA.

tEOREMA 3.3.4. pUSTX W NEKOTOROJ PROKOLOTOJ OKRESTNOSTI TO^KI x0 DLQ FUNKCIJ f(x), g(x) I h(x) WYPOLNQ@TSQ NERAWENSTWA

	f(x) 6 g(x) 6 h(x):	(3.3.2)
eSLI lim f(x) =	lim h(x) (PREDPOLAGAETSQ SU]ESTWOWANIE PRE-
x!x0	x!x0

DELOW I IH RAWENSTWO), TO PREDEL lim g(x) SU]ESTWUET I RAWEN

x!x0

lim f(x).

x!x0

dOKAZATELXSTWO. wOZXMEM PROIZWOLXNU@ SHODQ]U@SQ K x0 POSLE- DOWATELXNOSTX fxng IZ PROKOLOTOJ OKRESTNOSTI TO^KI x0, W KOTOROJ WYPOLNQ@TSQ NERAWENSTWA (3.3.2). tOGDA f(xn) 6 g(xn) 6 h(xn) I PREDELY POSLEDOWATELXNOSTEJ ff(xn)g I fh(xn)g SU]ESTWU@T I RAW-

lim g(xn) = lim f(xn):

n!1 n!1

oTS@DA, POLXZUQSX OPREDELENIEM PREDELA FUNKCII PO gEJNE, PRIHODIM K UTWERVDENI@ TEOREMY.

51

tEOREMA 3.3.5. eSLI SU]ESTWUET PREDEL lim f(x), TO SU]EST-

x!x0

WUET PREDEL lim jf(x)j I SPRAWEDLIWO RAWENSTWO

x!x0

lim jf(x)j = lim f(x) :

x!x0 x!x0

dOKAZATELXSTWO. pUSTX lim f(x) = a. zNA^IT, DLQ KAVDOGO " > 0

x!x0

SU]ESTWUET TAKOE > 0, ^TO DLQ WSEH x, DLQ KOTORYH 0 < jx;x0j < ,

IMEEM jf(x) ; aj < ".

nO TOGDA jf(x)j ; jaj 6 jf(x) ; aj < " I TEOREMA DOKAZANA.

rASSMOTRIM ARIFMETI^ESKIE DEJSTWIQ NAD FUNKCIQMI, IME@- ]IMI PREDELY.

tEOREMA 3.3.6. pUSTX DLQ FUNKCIJ f I g SU]ESTWU@T PREDELY

lim f(x) I	lim g(x). tOGDA SU]ESTWU@T UKAZANNYE NIVE PREDELY
x!x0	x!x0
I WYPOLNQ@TSQ RAWENSTWA:
	lim [f(x)				g(x)] =		lim f(x)			lim g(x)
	x!x0						x!x0		x!x0
	lim f(x)				g(x) =		lim f(x)		lim g(x)
	x!x0						x!x0		x!x0
ESLI, KROME TOGO,		lim g(x) = 0, TO
		x!x0				6
						f(x)		lim f(x)
			lim				=	x!x0		:
						g(x)		lim g(x)
		x!x0
								x!x0
dOKAZATELXSTWO.		zAMETIM, ^TO W UTWERVDENII O ^ASTNOM IZ USLO-

WIQ lim g(x) 6= 0 SOGLASNO TEOREME 3.3.2 SLEDUET, ^TO W NEKOTOROJ

x!x0

PROKOLOTOJ OKRESTNOSTI TO^KI x0 WYPOLNQETSQ NERAWENSTWO g(x) =6 0, ZNA^IT, W \TOJ OKRESTNOSTI IMEET SMYSL ^ASTNOE f(x)=g(x).

dOKAZATELXSTWO KAVDOGO IZ UTWERVDENIJ TEOREMY PROWODITSQ PO SLEDU@]EJ SHEME. wYBIRAETSQ PROIZWOLXNAQ SHODQ]AQSQ K x0 POSLEDOWATELXNOSTX TO^EK fxng IZ PROKOLOTOJ OKRESTNOSTI TO^KI x0, W KOTOROJ OPREDELENY FUNKCII f I g. dLQ ^ISLOWYH POSLEDOWA- TELXNOSTEJ ff(xn)g I fg(xn)g SOOTWETSTWU@]IE SWOJSTWA IZWESTNY (KOGDA GOWORITSQ O ^ASTNOM, U^ITYWAEM, ^TO g(xn) 6= 0 DLQ DOSTA- TO^NO BOLX[IH n). pRI \TOM DLQ L@BOJ POSLEDOWATELXNOSTI fxng UKAZANNOGO WIDA W LEWOJ ^ASTI RAWENSTW KAVDOGO IZ UTWERVDENIJ TEOREMY POLU^AEM ODNI I TE VE ZNA^ENIQ PREDELOW, TAK KAK PREDELY W PRAWYH ^ASTQH NE ZAWISQT OT TOGO, KAKAQ IMENNO POSLEDOWATELX- NOSTX fxng BYLA WZQTA.

tAKIM OBRAZOM, TEOREMA DOKAZANA.

52

x 3.4. kRITERIJ kO[I

tEOREMA 3.4.1 (kRITERIJ kO[I). pUSTX FUNKCIQ f OPREDELENA W NEKOTOROJ PROKOLOTOJ OKRESTNOSTI TO^KI x0. dLQ TO-

GO ^TOBY SU]ESTWOWAL KONE^NYJ PREDEL lim f(x), NEOBHODIMO I

x!x0

DOSTATO^NO, ^TOBY WYPOLNQLOSX USLOWIE kO[I, T.E. ^TOBY DLQ

KAVDOGO " > 0 SU]ESTWOWALO TAKOE > 0, ^TO DLQ L@BYH TO-

^EK x0 I x00

IZ PROKOLOTOJ -OKRESTNOSTI TO^KI x0 IMELO MESTO

NERAWENSTWO

jf(x0) ; f(x00)j < ":

(3.4.1)

dOKAZATELXSTWO.

pUSTX lim

f(x) = a. dLQ KAVDOGO " > 0 NAHODIM

> 0

,

x!x0

0 < jx ; x0j < ,

-

TAKOE

^TO DLQ WSEH

x,

DLQ KOTORYH

WYPOLNQ

0

00

j

;

j

ETSQ NERAWENSTWO

f(x)

a < "=2. wZQW TEPERX PROIZWOLNYE TO^KI

x I x

IZ \TOJ PROKOLOTOJ -OKRESTNOSTI, WIDIM,

^TO

jf(x0) ; f(x00)j 6 jf(x0) ; aj + ja ; f(x00)j <

"

"

2 +

2 = "

I NEOBHODIMOSTX USLOWIQ kO[I DOKAZANA.

pUSTX TEPERX WYPOLNENO USLOWIE kO[I. pO " > 0 WYBIRAEM TA-

KOE > 0, ^TO DLQ L@BYH TO^EK x0 I x00 IZ PROKOLOTOJ -OKRESTNOSTI

TO^KI x0 SPRAWEDLIWO NERAWENSTWO (3.4.1).

rASSMOTRIM PROIZWOLXNU@ POSLEDOWATELXNOSTX TO^EK fxng

IZ

OBLASTI OPREDELENIQ FUNKCII f TAKU@, ^TO xn

6= x0 DLQ WSEH

n

I xn ! x0, n ! 1. w SILU SHODIMOSTI xn K x0 SU]ESTWUET ^ISLO N,

ZAWISQ]EE OT , A W KONE^NOM S^ETE ZAWISQ]EE OT ", TAKOE, ^TO DLQ

WSEH n > N TO^KI xn PRINADLEVAT TOJ PROKOLOTOJ -OKRESTNOSTI

TO^KI x0, GDE WYPOLNQETSQ NERAWENSTWO (3.4.1).

tOGDA DLQ n, m > N IMEEM jf(xn) ;f(xm)j < ". |TO POKAZYWAET,

^TO WYPOLNENO USLOWIE kO[I DLQ POSLEDOWATELXNOSTI ff(xn)g. tA-

KIM OBRAZOM, DLQ L@BOJ POSLEDOWATELXNOSTI fxng

RASSMATRIWAEMO-

GO WIDA SU]ESTWUET KONE^NYJ PREDEL POSLEDOWATELXNOSTI ff(xn)g.

nUVNO E]E POKAZATX, ^TO DLQ RAZNYH POSLEDOWATELXNOSTEJ fxng

PREDELY POSLEDOWATELXNOSTEJ ff(xn)g ODINAKOWY.

rASSMOTRIM DWE POSLEDOWATELXNOSTI UKAZANNOGO WIDA fxng

I

ftng. pUSTX limn!1 f(xn) = a I limn!1 f(tn) = b. sOSTAWIM NO-

WU@ POSLEDOWATELXNOSTX

x1 t1 x2 t2 x3 t3 : : :

(3.4.2)

WKL@^AQ W NEE POPEREMENNO ^LENY POSLEDOWATELXNOSTEJ fxng I ftng.

53

wSE ^LENY POSLEDOWATELXNOSTI (3.4.2) PRINADLEVAT OBLASTI OPREDELENIQ FUNKCII f, OTLI^NY OT x0 I POSLEDOWATELXNOSTX (3.4.2) SHODITSQ K x0. zNA^IT, PO UVE DOKAZANNOMU POSLEDOWATELXNOSTX ZNA- ^ENIJ FUNKCII f W TO^KAH \TOJ POSLEDOWATELXNOSTI IMEET PREDEL. ~ISLA a I b QWLQ@TSQ ^ASTI^NYMI PREDELAMI \TOJ SHODQ]EJSQ PO- SLEDOWATELXNOSTI. oTS@DA SLEDUET, ^TO a = b.

tEOREMA DOKAZANA.

x 3.5. pREDEL SLOVNOJ FUNKCII

sNA^ALA OB_QSNIM TERMIN \SLOVNAQ FUNKCIQ".

oPREDELENIE. pUSTX NA MNOVESTWE D ZADANA FUNKCIQ f(x) I E | MNOVESTWO ZNA^ENIJ FUNKCII f. pREDPOLOVIM, ^TO NA E OPREDELENA FUNKCIQ '. tOGDA DLQ WSEH x 2 D IMEET SMYSL WYRAVENIE

(x) := '(f(x)):

zADANNAQ TAKIM OBRAZOM NA D FUNKCIQ	NAZYWAETSQ SLOVNOJ
FUNKCIEJ.

sLOVNU@ FUNKCI@ NAZYWA@T TAKVE FUNKCIEJ OT FUNKCII, SU- PERPOZICIEJ FUNKCIJ ILI KOMPOZICIEJ FUNKCIJ.

rASSMOTRIM WOPROS, PRI KAKIH USLOWIQH IZ SU]ESTWOWANIQ PRE- DELOW FUNKCIJ f I ' SLEDUET, ^TO IMEET PREDEL SLOVNAQ FUNKCIQ .

tEOREMA 3.5.1. pUSTX lim f(x) = y0, PRI^EM W NEKOTOROJ PRO-
x!x0
KOLOTOJ OKRESTNOSTI TO^KI x0
f(x) 6= y0:	(3.5.1)
pUSTX, DALEE, lim '(y) = z0. tOGDA SU]ESTWUET PREDEL
y!y0

lim '(f(x)) = z0:

x!x0

dOKAZATELXSTWO. zAMETIM, ^TO W DOKAZATELXSTWE NUVDAETSQ I TOT FAKT, ^TO SLOVNAQ FUNKCIQ '(f(x)) OPREDELENA W NEKOTOROJ PROKO- LOTOJ OKRESTNOSTI TO^KI x0. |TO BUDET USTANOWLENO PO HODU RAS- SUVDENIJ.

tAK KAK PREDEL FUNKCII ' W TO^KE y0 RAWEN z0, TO DLQ PROIZ- WOLXNOGO " > 0 SU]ESTWUET ^ISLO (") > 0 TAKOE, ^TO DLQ WSEH y, UDOWLETWORQ@]IH USLOWI@ 0 < jy ; y0j < , SPRAWEDLIWA OCENKA j'(y) ; z0j < ".

54

tEPERX PO NAHODIM > 0 TAKOE, ^TO DLQ WSEH x, DLQ KOTORYH

0 < jx;x0j < , IMEEM jf(x);y0j < . uMENX[IW W SLU^AE NEOBHODI- MOSTI ZNA^ENIE , MOVNO DOBITXSQ TOGO, ^TO W PROKOLOTOJ -OKREST-

NOSTI TO^KI x0 WYPOLNQETSQ USLOWIE (3.5.1). tOGDA WSE ZNA^ENIQ FUNKCII f DLQ x IZ \TOJ -OKRESTNOSTI PRINADLEVAT PROKOLOTOJ-OKRESTNOSTI TO^KI y0. zNA^IT, DLQ \TIH x

j'(f(x)) ; z0j < ":

oTS@DA SLEDUET UTWERVDENIE TEOREMY, POSKOLXKU WYBIRALOSX W ZAWISIMOSTI OT , A W ZAWISIMOSTI OT ", T.E. W KONCE KONCOW WYBORZAWISIT OT ".

uSLOWIE (3.5.1) SU]ESTWENNO DLQ SPRAWEDLIWOSTI TEOREMY 3.5.1. w SAMOM DELE, IZ SU]ESTWOWANIQ PREDELA limy!y0 '(y) NE SLEDUET, ^TO FUNKCIQ '(y) OPREDELENA W TO^KE y0, A ESLI I OPREDELENA, TO NIKAKIH USLOWIJ NA EE ZNA^ENIE W \TOJ TO^KE NE NAKLADYWAETSQ.

pO\TOMU, ESLI USLOWIE (3.5.1) NE WYPOLNENO, TO W KAK UGODNO MA- LOJ OKRESTNOSTI TO^KI x0 MOGUT OKAZATXSQ TO^KI x, DLQ KOTORYH WY- RAVENIE '(f(x)) ILI NE OPREDELENO ILI PRINIMAET ZNA^ENIQ, NIKAK NE SWQZANNYE SO ZNA^ENIQMI ' W PROKOLOTOJ OKRESTNOSTI TO^KI y0. wMESTE S TEM, IZ DOKAZATELXSTWA TEOREMY 3.5.1 WIDNO, ^TO OT USLOWIQ (3.5.1) MOVNO OTKAZATXSQ, ESLI POTREBOWATX, ^TO FUNKCIQ

' OPREDELENA PRI y = y0 I lim '(y) = '(y0).

y!y0

tAKIM OBRAZOM, IMEET MESTO SLEDU@]EE UTWERVDENIE.

tEOREMA 3.5.2.	pUSTX lim f(x) = y0 I	lim '(y) = '(y0). tOGDA
	x!x0	y!y0

lim '(f(x)) = '(y0):

x!x0

x 3.6. oDNOSTORONNIE PREDELY

nARQDU S OKRESTNOSTQMI TO^EK, KOGDA TO^KA LEVIT WNUTRI SOOT- WETSTWU@]EGO INTERWALA, RASSMATRIWA@TSQ PROMEVUTKI, KOTORYE NAZYWA@T ODNOSTORONNIMI OKRESTNOSTQMI TO^EK. l@BOJ POLUOTRE- ZOK WIDA (a x0] NAZYWA@T LEWOJ OKRESTNOSTX@ TO^KI x0, A POLUOT- REZOK WIDA [x0 b) | PRAWOJ OKRESTNOSTX@ TO^KI x0.

w TERMINAH LEWYH I PRAWYH OKRESTNOSTEJ WWODQTSQ ODNOSTORON- NIE PREDELY. pRIWEDEM OPREDELENIE PREDELA FUNKCII W TO^KE SPRA- WA.

oPREDELENIE. pUSTX FUNKCIQ f ZADANA W NEKOTOROJ PRAWOJ OKRESTNOSTI TO^KI x0, ZA ISKL@^ENIEM, BYTX MOVET, SAMOJ TO^KI x0. ~ISLO a NAZYWAETSQ PREDELOM FUNKCII f W TO^KE x0 SPRAWA,

55

f(x) 6 M:

ESLI DLQ KAVDOGO " > 0 SU]ESTWUET = (") > 0 TAKOE, ^TO DLQ WSEH x, UDOWLETWORQ@]IH USLOWI@ x0 < x < x0 + , SPRAWEDLIWA OCENKA

jf(x) ; aj < ":

w \TOM SLU^AE PI[UT

a =	lim	f(x) =	lim f(x)
	x!x0 x>x0		x!x0+0

ILI a = f(x0 + 0).

|TO | OPREDELENIE PREDELA PO kO[I. mOVNO DATX OPREDELENIE ODNOSTORONNIH PREDELOW PO gEJNE I DOKAZATX IH \KWIWALENTNOSTX. nE BUDEM NA \TOM OSTANAWLIWATXSQ WWIDU O^EWIDNOSTI TEH IZME- NENIJ, KOTORYE NUVNO SDELATX PO SRAWNENI@ SO SLU^AEM OBY^NYH PREDELOW.

sOOTWETSTWU@]IM OBRAZOM FORMULIRUETSQ OPREDELENIE PREDELA FUNKCII SLEWA. |TOT PREDEL OBOZNA^A@T f(x0 ;0). pRAWYJ I LEWYJ PREDELY W TO^KE 0 OBOZNA^A@T f(+0) I f(;0).

pONQTNO, ^TO SU]ESTWOWANIE PREDELA lim f(x) RAWNOSILXNO SU-

x!x0

]ESTWOWANI@ I RAWENSTWU ODNOSTORONNIH PREDELOW f(x0+0) I f(x0;

0).

tEOREMA 3.6.1. pUSTX FUNKCIQ f WOZRASTAET NA INTERWALE (a b),

T.E. f(x1) 6 f(x2) DLQ x1 < x2. tOGDA ESLI ZNA^ENIQ f NA (a b) OGRANI^ENY SWERHU ^ISLOM B, TO PREDEL f(b ; 0) SU]ESTWUET I

f(b ; 0) 6 B. eSLI FUNKCIQ f NE QWLQETSQ OGRANI^ENNOJ SWERHU NA

(a b), TO f(b ; 0) = +1.

dOKAZATELXSTWO. rASSUVDENIQ ANALOGI^NY DOKAZATELXSTWU SOOT- WETSTWU@]EJ TEOREMY DLQ POSLEDOWATELXNOSTEJ. eSLI f(x) 6 B

DLQ x	2	(a b), TO SU]ESTWUET M := sup f(x) I M 6 B. tAK KAK
		x2(a b)
M | TO^NAQ WERHNQQ GRANX, TO DLQ KAVDOGO " > 0 NAJDETSQ TO^KA

x" 2 (a b), DLQ KOTOROJ f(x") > M ;". nO TOGDA W SILU WOZRASTANIQ f DLQ WSEH x 2 (x" b) IMEEM

M ; " < f(x") 6

a \TO POKAZYWAET, ^TO f(b ; 0) = M.

eSLI f NE QWLQETSQ OGRANI^ENNOJ SWERHU, TO DLQ KAVDOGO ^ISLA L SU]ESTWUET TO^KA xL 2 (a b) TAKAQ, ^TO f(xL) > L. a W SILU WOZRASTANIQ f DLQ WSEH x 2 (xL b) IMEEM f(x) > f(xL) > L. zNA^IT, f(b ; 0) = +1.

tEOREMA DOKAZANA.

56

(3.7.1) x0. hOTQ W \TOJ

aNALOGI^NOE UTWERVDENIE SPRAWEDLIWO I DLQ UBYWA@]IH FUNK- CIJ.

tEOREMA 3.6.2. eSLI FUNKCIQ f MONOTONNA (T.E. WOZRASTAET ILI UBYWAET) NA (a b), TO DLQ KAVDOGO x 2 (a b) SU]ESTWU@T PREDELY f(x + 0) I f(x ; 0). pRI \TOM, ESLI f WOZRASTAET, TO f(x ; 0) 6 f(x + 0), A ESLI f UBYWAET, TO f(x ; 0) > f(x + 0).

dOKAZATELXSTWO. pUSTX f NA (a b) WOZRASTAET. dLQ KAVDOJ TO^KI x0 RASSMOTRIM SLED f NA INTERWALE (a x0).

tAK KAK WSE ZNA^ENIQ FUNKCII f NA (a x0) OGRANI^ENY SWERHU ^ISLOM f(x0), TO SOGLASNO TEOREME 3.6.1 SU]ESTWUET PREDEL f(x0 ; 0) I SPRAWEDLIWO NERAWENSTWO f(x0 ; 0) 6 f(x0). tO^NO TAK VE IZ WOZRASTANIQ f NA INTERWALE (x0 b) SLEDUET SU]ESTWOWANIE PREDELA f(x0 + 0) I NERAWENSTWO f(x0) 6 f(x0 + 0). |TO DOKAZYWAET TEOREMU DLQ WOZRASTA@]IH FUNKCIJ.

dLQ UBYWA@]IH FUNKCIJ RASSUVDENIQ ANALOGI^NY.

x 3.7. sRAWNENIE FUNKCIJ

pUSTX NA MNOVESTWE D ZADANY FUNKCII f(x) I '(x). eSLI SU- ]ESTWUET TAKOE ^ISLO C, ^TO DLQ WSEH x 2 D WYPOLNQETSQ NERAWEN- STWO

jf(x)j 6 Cj'(x)j

TO PI[UT

f(x) = O('(x)) NA D

I GOWORQT, ^TO f ESTX O-BOLX[OE OT ' NA D.

pUSTX TEPERX FUNKCII f(x) I '(x) ZADANY W NEKOTOROJ PROKO- LOTOJ OKRESTNOSTI TO^KI x0. eSLI SU]ESTWU@T ^ISLO C I TAKAQ PROKOLOTAQ OKRESTNOSTX TO^KI x0, ^TO DLQ WSEH x IZ \TOJ OKREST- NOSTI

jf(x)j 6 Cj'(x)j

TO PI[UT

f(x) = O('(x)) x ! x0

I GOWORQT, ^TO f ESTX O-BOLX[OE OT ' PRI x !

FORMULE ISPOLXZOWANA ZAPISX x ! x0, NO NIKAKOGO PREDELXNOGO PE- REHODA ZDESX NET. |TO OZNA^AET TOLXKO, ^TO RE^X IDET O DOSTATO^NO MALOJ OKRESTNOSTI TO^KI x0.

eSLI NA D ILI PRI x ! x0 ODNOWREMENNO IME@T MESTO SOOTNO- [ENIQ f(x) = O('(x)) I '(x) = O(f(x)), TO GOWORQT, ^TO FUNKCII

57

f(x) I '(x) IME@T ODINAKOWYJ PORQDOK, SOOTWETSTWENNO, NA D ILI

PRI x ! x0.

oBOZNA^ATX \TO BUDEM TAK:

f(x) '(x)

(3.7.2)

DOBAWLQQ, ^TO \TO SOOTNO[ENIE IMEET MESTO NA D ILI PRI x ! x0. eSLI FUNKCII f(x) I '(x) NE OBRA]A@TSQ W NULX (SOOTWETSTWEN- NO, NA D ILI W NEKOTOROJ PROKOLOTOJ OKRESTNOSTI TO^KI x0), TO OPREDELENIE ODINAKOWOGO PORQDKA \TIH FUNKCIJ MOVNO SFORMULI- ROWATX TAK: SU]ESTWU@T POLOVITELXNYE ^ISLA C1 I C2 TAKIE, ^TO

f(x)

C1 6 '(x) 6 C2

NA D ILI W DOSTATO^NO MALOJ PROKOLOTOJ OKRESTNOSTI TO^KI x0. rASSMOTRIM FUNKCII f(x) I '(x), ZADANNYE W NEKOTOROJ PROKO-

LOTOJ OKRESTNOSTI TO^KI x0, DLQ KOTORYH

lim f(x) = 0:

x!x0 '(x)

w \TOM SLU^AE PI[UT

f(x) = o('(x)) x ! x0

(3.7.3)

I GOWORQT, ^TO FUNKCIQ f(x) ESTX o-MALOE OT '(x) PRI x ! x0. eSLI f(x) = o(1), x ! x0, TO FUNKCI@ f NAZYWA@T BESKONE^NO

MALOJ (IS^EZA@]EJ) PRI x ! x0.

qSNO, ^TO ESLI f(x) = o('(x)), x ! x0, TO f(x) = O('(x)), x ! x0, A OBRATNOE UTWERVDENIE NE WERNO.

pONQTNO TAKVE, ^TO ESLI f(x) = O('(x)), x ! x0, I '(x) = O( (x)), x ! x0, TO f(x) = O( (x)), x ! x0, PRI^EM ESLI HOTQ BY W ODNOM IZ ISHODNYH SOOTNO[ENIJ ZAMENITX O NA o, TO POLU^IM

f(x) = o( (x)), x ! x0.

eSLI FUNKCII f(x) I '(x) TAKOWY, ^TO

lim f(x) = 1

x!x0 '(x)

TO GOWORQT, ^TO FUNKCII f(x) I '(x) PRI x	! x0 ASIMPTOTI^ESKI
RAWNY ILI \KWIWALENTNY. w TAKOM SLU^AE BUDEM PISATX
f(x) '(x) x ! x0:	(3.7.4)

58

k SOVALENI@, NET USTANOWIW[IHSQ OB]EPRINQYH OBOZNA^ENIJ DLQ PORQDKOWOGO I ASIMPTOTI^ESKOGO RAWENSTW I NARQDU S (3.7.2) I (3.7.4) ISPOLXZU@TSQ I DRUGIE WARIANTY ZAPISI.

oTMETIM, ^TO OPREDELENIQ SIMWOLOW O, o, , MOVNO OTNOSITX NE KO WSEJ OKRESTNOSTI TO^KI x0, A K ODNOSTORONNIM OKRESTNOSTQM. pOD^ERKNEM, ^TO HOTQ W FORMULAH (3.7.1) I (3.7.3) UPOTREBLQET- SQ ZNAK RAWENSTWA, W OBOIH \TIH SLU^AQH MY IMEEM DELO NE S RAWEN- STWAMI, A S OCENKAMI, SRAWNIWA@]IMI POWEDENIE FUNKCII f(x) S

POWEDENIEM FUNKCII '(x) PRI x ! x0.

gLAWA 4

neprerywnye funkcii

x 4.1. nEPRERYWNOSTX FUNKCII W TO^KE

oPREDELENIE. fUNKCIQ f NAZYWAETSQ NEPRERYWNOJ W TO^KE x0, ESLI ONA OPREDELENA W NEKOTOROJ OKRESTNOSTI \TOJ TO^KI I DLQ KAV- DOGO " > 0 SU]ESTWUET = (") > 0 TAKOE, ^TO DLQ WSEH x, UDOWLE- TWORQ@]IH USLOWI@ jx ; x0j < , SPRAWEDLIWO NERAWENSTWO

jf(x) ; f(x0)j < ":

iSPOLXZUQ PREDEL FUNKCII W TO^KE, MOVNO DATX \KWIWALENTNU@ FORMULIROWKU: FUNKCIQ f NEPRERYWNA W TO^KE x0, ESLI

lim f(x) = f(x0):

x!x0

gRAFI^ESKI NEPRERYWNOSTX f W TO^KE x0 OZNA^AET, ^TO PO " > 0 STROITSQ POLOSA, PARALLELXNAQ OSI OX, ZAKL@^ENNAQ MEVDU PRQMY- MI y = f(x0) + " I y = f(x0) ; ", I TREBUETSQ, ^TOBY SU]ESTWOWALA TAKAQ -OKRESTNOSTX TO^KI x0, ^TO DLQ WSEH x IZ \TOJ OKRESTNOSTI TO^KI GRAFIKA FUNKCII f(x) POPADALI W UKAZANNU@ POLOSU.

mOVNO DATX OPREDELENIE I W TERMINAH POSLEDOWATELXNOSTEJ: FUNKCIQ f NEPRERYWNA W TO^KE x0, ESLI ONA OPREDELENA W NEKOTO- ROJ OKRESTNOSTI \TOJ TO^KI I DLQ L@BOJ POSLEDOWATELXNOSTI TO^EK

fxng IZ OBLASTI OPREDELENIQ f TAKOJ, ^TO nlim!1 xn = x0, SPRAWELIWO

RAWENSTWO nlim!1 f(xn) = f(x0). |TO MOVNO ZAPISATX TAK:

lim f(xn) = f( lim xn):

n!1 n!1

59

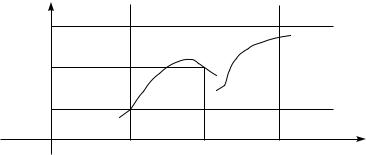
y

f(x0)+ε

y=f(x)

f(x0)

f(x0)–ε

x –δ	x	0	x +δ	x
0			0

pRI OBSUVDENII WOPROSOW, SWQZANNYH S NEPRERYWNOSTX@ FUNK- CIJ, UDOBNO POLXZOWATXSQ PONQTIEM PRIRA]ENIQ FUNKCII. dADIM ARGUMENTU x0 FUNKCII y = f(x) PRIRA]ENIE x TAK, ^TOBY ^ISLO x0 + x TAKVE PRINADLEVALO OBLASTI OPREDELENIQ FUNKCII. pRIRA- ]ENIE x MOVET BYTX KAK POLOVITELXNYM, TAK I OTRICATELXNYM. rAZNOSTX ZNA^ENIJ FUNKCII

y := f(x0 + x) ; f(x0)

NAZYWAETSQ PRIRA]ENIEM FUNKCII f W TO^KE x0, SOOTWETSTWU@]IM PRIRA]ENI@ ARGUMENTA x.

nEPRERYWNOSTX FUNKCII f W TO^KE x0 \KWIWALENTNA TOMU, ^TO

y ! 0 PRI x ! 0.

pERE^ISLIM SWOJSTWA NEPRERYWNYH FUNKCIJ, KOTORYE WYTEKA- @T IZ SWOJSTW PREDELA FUNKCII W TO^KE.

eSLI FUNKCIQ NEPRERYWNA W TO^KE, TO ONA OGRANI^ENA W NEKOTO- ROJ OKRESTNOSTI \TOJ TO^KI.

eSLI FUNKCIQ f NEPRERYWNA W TO^KE x0 I f(x0) =6 0, TO SU]EST- WUET TAKAQ OKRESTNOSTX TO^KI x0, ^TO jf(x)j > jf(x0)j=2 DLQ WSEH x IZ \TOJ OKRESTNOSTI. pRI \TOM f(x) > f(x0)=2, ESLI f(x0) > 0, I

f(x) < f(x0)=2, ESLI f(x0) < 0.

oTS@DA SLEDUET, ^TO ESLI FUNKCIQ f NEPRERYWNA W TO^KE x0 I f(x0) 6= 0, TO f SOHRANQET ZNAK W NEKOTOROJ OKRESTNOSTI TO^KI x0.

eSLI FUNKCII f(x) I g(x) NEPRERYWNY W TO^KE x0, TO W \TOJ TO^KE NEPRERYWNY FUNKCII f(x) + g(x), f(x) ; g(x), f(x) g(x), A ESLI, KROME TOGO, g(x0) 6= 0, TO NEPRERYWNA I FUNKCIQ f(x)=g(x).

nEPRERYWNOSTX FUNKCIJ, POLU^ENNYH PRI ARIFMETI^ESKIH DEJ- STWIQH NAD NEPRERYWNYMI FUNKCIQMI, POZWOLQET SDELATX WYWOD O NEPRERYWNOSTI MNOGO^LENOW. w SAMOM DELE, NEPRERYWNOSTX FUNKCIJ f(x) = C (\TA FUNKCIQ PRINIMAET ZNA^ENIE C DLQ WSEH ZNA^ENIJ AR- GUMENTA) I f(x) = x O^EWIDNA. zNA^IT, DLQ KAVDOGO NATURALXNOGO

60