Матан, Лекции - Теляковский 1

IV. dLQ KAVDOGO NEPUSTOGO OGRANI^ENNOGO SWERHU MNOVESTWA SU- ]ESTWUET ^ISLO, QWLQ@]EESQ EGO TO^NOJ WERHNEJ GRANX@.

sWOJSTWO NEPRERYWNOSTI MOVNO WYRAZITX I W DRUGIH TERMINAH. mY POZNAKOMIMSQ E]E S FORMULIROWKOJ W TERMINAH POSLEDOWATELX- NOSTEJ WLOVENNYH OTREZKOW.

x 1.7. pOSLEDOWATELXNOSTI WLOVENNYH OTREZKOW

nAPOMNIM OPREDELENIQ ^ISLOWYH PROMEVUTKOW, DAWAW[IESQ W [KOLE.

eSLI a < b, TO MNOVESTWO ^ISEL x, UDOWLETWORQ@]IH NERAWEN- STWAM a 6 x 6 b, NAZYWA@T OTREZKOM (^ISLOWYM OTREZKOM) I OBO- ZNA^A@T [a b]. tO^KI a I b NAZYWA@T KONCAMI OTREZKA, A DLINOJ OTREZKA NAZYWA@T ^ISLO b ; a.

mNOVESTWO ^ISEL x, UDOWLETWORQ@]IH NERAWENSTWAM a < x < b, NAZYWA@T INTERWALOM (S KONCAMI W TO^KAH a I b) I OBOZNA^A@T (a b). ~ISLO b ; a NAZYWA@T DLINOJ INTERWALA. wSTRE^A@]EESQ W NEKOTORYH RUKOWODSTWAH OBOZNA^ENIE DLQ INTERWALA ]a b[ NE PRI- VILOSX.

rASSMATRIWA@T TAKVE POLUOTREZKI [a b), KOGDA a 6 x < b, I (a b], KOGDA a < x 6 b. iH NAZYWA@T TAKVE POLUINTERWALAMI.

tAKIM OBRAZOM, KWADRATNU@ SKOBKU PI[UT, ESLI SOOTWETSTWU@- ]AQ KONCEWAQ TO^KA PRINADLEVIT PROMEVUTKU, INA^E PI[UT KRUG- LU@ SKOBKU.

oBOZNA^ENIQ DLQ BESKONE^NYH PROMEVUTKOW: MNOVESTWO ^ISEL x, DLQ KOTORYH x > a, OBOZNA^A@T [a +1) DLQ KOTORYH x > a, OBOZNA^A@T (a +1) DLQ KOTORYH x 6 a, OBOZNA^A@T (;1 a] DLQ KOTORYH x < a, OBOZNA^A@T (;1 a). nAKONEC, WSE ^ISLA OBRAZU@T

INTERWAL (;1, +1). ( , - oTREZKI INTERWALY I POLUOTREZKI KAK KONE^NYE TAK I BESKO

NE^NYE) BUDEM NAZYWATX PROMEVUTKAMI.

eSLI [a b] [c d], TO GOWORQT, ^TO OTREZOK [a b] WLOVEN W OTREZOK

[c d].

dADIM TEPERX OPREDELENIE POSLEDOWATELXNOSTI.

oPREDELENIE. eSLI KAVDOMU NATURALXNOMU ^ISLU n POSTAWLEN W SOOTWETSTWIE NEKOTORYJ \LEMENT MNOVESTWA A, KOTORYJ BUDEM OBO- ZNA^ATX xn, TO GOWORQT, ^TO \LEMENTY

x1 x2 x3 : : :

OBRAZU@T POSLEDOWATELXNOSTX.

|TU POSLEDOWATELXNOSTX OBOZNA^A@T fxng1n=1 ILI PROSTO fxng.

21

|LEMENTY, SOSTAWLQ@]IE POSLEDOWATELXNOSTX, NAZYWA@T ^LENA-

MI POSLEDOWATELXNOSTI.

w \TOM OPREDELENII NUMERACIQ ^LENOW POSLEDOWATELXNOSTI xn NA^INAETSQ S n = 1. |TO NE OBQZATELXNO, INOGDA BYWAET UDOBNO NA^INATX NUMERACI@ S NULQ. mOVNO WOOB]E NA^INATX NUMERACI@ S PROIZWOLXNOGO CELOGO ^ISLA.

oTMETIM, ^TO W OTLI^IE OT [KOLXNOGO OPREDELENIQ MY S^ITAEM POSLEDOWATELXNOSTI BESKONE^NYMI.

~LENY POSLEDOWATELXNOSTI xn I xm PRI n =6 m NE OBQZATELXNO DOLVNY BYTX RAZNYMI \LEMENTAMI MNOVESTWA A. bOLEE TOGO, WSE ^LENY POSLEDOWATELXNOSTI MOGUT BYTX ODNIM I TEM VE \LEMENTOM. tAKIE POSLEDOWATELXNOSTI NAZYWA@T STACIONARNYMI.

oPREDELIM ^ISLOWYE POSLEDOWATELXNOSTI, SHODQ]IESQ K NUL@.

oPREDELENIE. gOWORQT, ^TO ^ISLOWAQ POSLEDOWATELXNOSTX x1 x2,

: : : SHODITSQ K NUL@, ESLI DLQ KAVDOGO POLOVITELXNOGO ^ISLA " SU]ESTWUET TAKOE (ZAWISQ]EE OT ") ^ISLO N, ^TO DLQ WSEH NOMEROW n > N SPRAWEDLIWO NERAWENSTWO

jxnj < ":

(1.7.1)

dRUGIMI SLOWAMI MOVNO SKAZATX, ^TO DLQ KAVDOGO " > 0 NE- RAWENSTWO (1.7.1) DOLVNO WYPOLNQTXSQ DLQ WSEH DOSTATO^NO BOLX- [IH n.

eSLI POSLEDOWATELXNOSTX fxng SHODITSQ K NUL@, TO GOWORQT, ^TO ^LENY \TOJ POSLEDOWATELXNOSTI (T.E. ^ISLA xn) STREMQTSQ K NUL@.

tEOREMA 1.7.1. pUSTX ZADANA POSLEDOWATELXNOSTX OTREZKOW [an bn], n = 1 2 : : : , GDE KAVDYJ SLEDU@]IJ OTREZOK WLOVEN W PREDYDU]IJ. eSLI POSLEDOWATELXNOSTX DLIN \TIH OTREZKOW SHODITSQ K NUL@, TO SU]ESTWUET I PRITOM TOLXKO ODNO ^ISLO, PRINADLEVA]EE WSEM OTREZKAM [an bn].

dOKAZATELXSTWO. tAK KAK WSE OTREZKI [an bn] SODERVATSQ W [a1 b1], TO POSLEDOWATELXNOSTX fang LEWYH KONCOW OTREZKOW OGRANI^ENA SWERHU ^ISLOM b1.

rASSMOTRIM ^ISLO c := supn an. sNA^ALA DOKAVEM, ^TO c PRINAD- LEVIT WSEM OTREZKAM [an bn], A ZATEM UBEDIMSQ, ^TO \TIM SWOJSTWOM OBLADAET TOLXKO ODNO ^ISLO.

pO OPREDELENI@ TO^NOJ WERHNEJ GRANI 8n IMEEM an 6 c. s DRU- GOJ STORONY, ESLI BY DLQ NEKOTOROGO k MY IMELI bk < c, TO PO OPREDELENI@ TO^NOJ WERHNEJ GRANI NA[ELSQ BY TAKOJ NOMER m, ^TO bk < am. nO TOGDA OTREZKI [ak bk] I [am bm] NE IMELI BY OB]IH TO^EK, ^TO PROTIWORE^IT USLOWI@, ^TO OTREZKI WLOVENY. iTAK, 8k IMEEM c 6 bk, ZNA^IT, c 2 [ak bk] DLQ WSEH k.

22

ZNA^ATX x $ x0.

dOKAVEM EDINSTWENNOSTX. pUSTX SU]ESTWU@T NERAWNYE MEVDU SOBOJ ^ISLA c I d, PRINADLEVA]IE WSEM OTREZKAM [an bn], I DLQ OPREDELENNOSTI c < d. tOGDA IZ USLOWIJ an 6 c I d 6 bn NAHODIM bn ; an > d ; c > 0 n = 1 2 : : :, T.E. POSLEDOWATELXNOSTX DLIN OTREZKOW NE SHODITSQ K NUL@. pOLU^ENNOE PROTIWORE^IE ZAWER[AET DOKAZATELXSTWO TEOREMY.

zAMETIM, ^TO W USLOWIQH \TOJ TEOREMY NELXZQ ZAMENITX OTREZKI

[an bn] NA INTERWALY (an bn).

w SAMOM DELE, DLQ POSLEDOWATELXNOSTI INTERWALOW (0 2;n) KAV- DYJ SLEDU@]IJ INTERWAL WLOVEN W PREDYDU]IJ I POSLEDOWATELX- NOSTX DLIN \TIH INTERWALOW f2;ng SHODITSQ K NUL@. nO NIKAKOE ^ISLO NE MOVET PRINADLEVATX WSEM \TIM INTERWALAM.

tEOREMA 1.7.1 POZWOLQET ZAKON^ITX ISSLEDOWANIE SWQZI DEJSTWI- TELXNYH ^ISEL I TO^EK ^ISLOWOJ PRQMOJ.

w x1.1 BYLO POKAZANO, KAK PO TO^KE NA ^ISLOWOJ PRQMOJ NAJ- TI SOOTWETSTWU@]U@ EJ BESKONE^NU@ DESQTI^NU@ DROBX. pRI RAS- SMOTRENII OBRATNOJ ZADA^I O POSTROENII TO^KI, SOOTWETSTWU@]EJ ZADANNOJ BESKONE^NOJ DESQTI^NOJ DROBI, BYLO POKAZANO, ^TO ISKO- MAQ TO^KA DOLVNA PRINADLEVATX WSEM OTREZKAM NEKOTOROJ POSLEDO- WATELXNOSTI WLOVENNYH OTREZKOW, DLINA KAVDOGO IZ KOTORYH W 10 RAZ MENX[E DLINY PREDYDU]EGO. nO WOPROS O SU]ESTWOWANII TA- KOJ TO^KI OSTAWALSQ OTKRYTYM. tEPERX MY ZNAEM, ^TO OB]AQ WSEM \TIM OTREZKAM TO^KA SU]ESTWUET. zNA^IT, KAVDOMU DEJSTWITELX- NOMU ^ISLU SOOTWETSTWUET I PRITOM TOLXKO ODNA TO^KA ^ISLOWOJ PRQMOJ.

wWEDEM PONQTIE WZAIMNO ODNOZNA^NOGO SOOTWETSTWIQ MEVDU MNO- VESTWAMI.

oPREDELENIE. gOWORQT, ^TO MEVDU MNOVESTWAMI A I A0 USTANOW-

LENO WZAIMNO ODNOZNA^NOE SOOTWETSTWIE, ESLI KAVDOMU \LEMENTU x 2 A POSTAWLEN W SOOTWETSTWIE \LEMENT x0 2 A0 I PRI \TOM KAV- DYJ \LEMENT MNOVESTWA A0 SOOTWETSTWUET I PRITOM TOLXKO ODNOMU \LEMENTU IZ MNOVESTWA A. tAKOE SOOTWETSTWIE \LEMENTOW BUDEM OBO-

iSPOLXZUQ \TO PONQTIE, MOVNO SKAZATX, ^TO MEVDU TO^KAMI ^I- SLOWOJ PRQMOJ I DEJSTWITELXNYMI ^ISLAMI USTANOWLENO WZAIMNO ODNOZNA^NOGO SOOTWETSTWIE. pO\TOMU ^ASTO TO^KI ^ISLOWOJ PRQMOJ NAZYWA@T ^ISLAMI I, NAOBOROT, ^ISLA NAZYWA@T TO^KAMI.

mY POLU^ILI TEOREMU 1.7.1 O WLOVENNYH OTREZKAH KAK SLEDSTWIE TEOREMY 1.3.1 O TO^NOJ WERHNEJ GRANI.

pOKAVEM, ^TO IZ TEOREMY O WLOVENNYH OTREZKAH MOVNO WYWESTI TEOREMU O TO^NOJ WERHNEJ GRANI.

pUSTX A | NEPUSTOE OGRANI^ENNOE SWERHU MNOVESTWO. zNA^IT,

23

SU]ESTWUET ^ISLO L TAKOE, ^TO 8x 2 A IMEEM x < L. wOZXMEM PROIZ- WOLXNOE ^ISLO x0 2 A I WWEDEM OTREZOK [a1 b1] := [x0 L]. zAMETIM, ^TO OTREZOK [a1 b1] SODERVIT TO^KI IZ A, A PRAWEE \TOGO OTREZKA TO^EK IZ A NET.

rAZDELIM OTREZOK [a1 b1] POPOLAM I OBOZNA^IM ^EREZ [a2 b2] TOT IZ POLU^ENNYH OTREZKOW, KOTORYJ SAM SODERVIT TO^KI IZ A, A PRA- WEE EGO TO^EK IZ A NET. pO POSTROENI@ b2 ; a2 = (b1 ; a1)=2.

nA SLEDU@]EM [AGE DELIM OTREZOK [a2 b2] POPOLAM I WYBIRAEM TAKOJ IZ OTREZO^KOW, ^TO SAM ON SODERVIT TO^KI IZ A, A PRAWEE EGO TO^EK IZ A NET.

pRODOLVIW \TOT PROCESS NEOGRANI^ENNO, POLU^IM POSLEDOWA-

TELXNOSTX WLOVENNYH OTREZKOW [a1 b1] [a2 b2] [a3 b3] : : : , KAV- DYJ IZ KOTORYH SODERVIT TO^KI IZ A, A PRAWEE EGO TO^EK IZ A NET.

kROME TOGO, PO POSTROENI@ bn;an = (b1;a1)=2n;1, ZNA^IT, POSLEDO- WATELXNOSTX DLIN OTREZKOW SHODITSQ K NUL@. pO TEOREME O WLOVEN- NYH OTREZKAH SU]ESTWUET EDINSTWENNAQ TO^KA c, PRINADLEVA]AQ WSEM \TIM OTREZKAM.

pOKAVEM, ^TO \TA TO^KA c = sup A.

1) dLQ WSEH x 2 A IMEEM x 6 c. dEJSTWITELXNO, ESLI BY SU]EST- WOWALA TO^KA x 2 A TAKAQ, ^TO x > c, TO MY WZQLI BY OTREZOK

[an bn], DLINA KOTOROGO MENX[E x ;c. t.E. x ;c > bn ; an, OTKUDA x > bn ; an + c. tAK KAK \TOT OTREZOK SODERVIT TO^KU c, TO an 6 c

I, ZNA^IT, x > bn. nO PO POSTROENI@ TO^EK MNOVESTWA A, LEVA]IH PRAWEE OTREZKOW [an bn], NET.

2) wOZXMEM PROIZWOLXNOE ^ISLO c0 < c I NAJDEM OTREZOK [an bn], DLINA KOTOROGO MENX[E c;c0. |TOT OTREZOK SODERVIT TO^KU c I, ZNA- ^IT, NE MOVET SODERVATX c0 (ZDESX, KAK I WY[E, PRIWEDENNOE RASSUV- DENIE NA GEOMETRI^ESKOM QZYKE LEGKO ZAPISATX W WIDE NERAWENSTW). nO W KAVDOM OTREZKE [an bn] ESTX TO^KI IZ A, ZNA^IT, PRAWEE TO^KI c0 ESTX HOTQ BY ODNA TO^KA IZ A.

iTAK, MY DOKAZALI, ^TO c = sup A.

tAKIM OBRAZOM, TEOREMA O TO^NOJ WERHNEJ GRANI I TEOREMA O WLOVENNYH OTREZKAH \KWIWALENTNY.

x 1.8. s^ETNYE I NES^ETNYE MNOVESTWA

rASSMATRIM WOPROSY, SWQZANNYE SO SRAWNENIEM MNOVESTW PO KO- LI^ESTWU SODERVA]IHSQ W NIH \LEMENTOW.

dLQ KONE^NYH MNOVESTW (T.E. MNOVESTW IZ KONE^NOGO ^ISLA \LE- MENTOW) ZADA^A RE[AETSQ PROSTO, TAK KAK KOLI^ESTWO \LEMENTOW KO- NE^NOGO MNOVESTWA WYRAVAETSQ NATURALXNYM ^ISLOM.

w SLU^AE, KOGDA NE IMEET ZNA^ENIQ, SKOLXKO IMENNO \LEMENTOW SO- DERVAT KONE^NYE MNOVESTWA A I B, A NUVNO ZNATX TOLXKO, W KAKOM

24

IZ NIH \LEMENTOW BOLX[E, UDOBNO ISPOLXZOWATX SLEDU@]EE SOOBRA- VENIE.

eSLI MOVNO USTANOWITX WZAIMNO ODNOZNA^NOE SOOTWETSTWIE MEV- DU \LEMENTAMI MNOVESTWA A I \LEMENTAMI NEKOTOROGO PODMNOVES- TWA MNOVESTWA B, TO ^ISLO \LEMENTOW MNOVESTWA A NE BOLX[E, ^EM ^ISLO \LEMENTOW W B.

tAKOJ PODHOD KLADETSQ W OSNOWU SRAWNENIQ KOLI^ESTWA \LEMENTOW BESKONE^NYH (T.E. NE QWLQ@]IHSQ KONE^NYMI) MNOVESTW. oPREDELENIE. gOWORQT, ^TO DWA MNOVESTWA IME@T ODINAKOWU@ MO]NOSTX (QWLQ@TSQ RAWNOMO]NYMI), ESLI MEVDU IH \LEMENTAMI MOVNO USTANOWITX WZAIMNO ODNOZNA^NOE SOOTWETSTWIE.

eSLI MNOVESTWO A IMEET ODINAKOWU@ MO]NOSTX S NEKOTORYM PODMNOVESTWOM MNOVESTWA B, TO GOWORQT, ^TO MO]NOSTX MNOVESTWA A MENX[E ILI RAWNA MO]NOSTI MNOVESTWA B.

oPREDELENIE. mNOVESTWO NAZYWAETSQ S^ETNYM, ESLI ONO IMEET ODINAKOWU@ MO]NOSTX S MNOVESTWOM NATURALXNYH ^ISEL.

zAMETIM, ^TO S^ETNOSTX MNOVESTWA \KWIWALENTNA WOZMOVNOSTI PREDSTAWITX WSE EGO \LEMENTY W WIDE POSLEDOWATELXNOSTI

a1 a2 a3 : : :

(1.8.1)

W KOTOROJ KAVDYJ \LEMENT MNOVESTWA U^ASTWUET ODIN RAZ. dEJSTWITELXNO, ESLI MNOVESTWO A S^ETNO, T.E. IMEETSQ WZAIMNO

ODNOZNA^NOE SOOTWETSTWIE \LEMENTOW A I N, TO MOVNO PREDSTAWITX WSE \LEMENTY MNOVESTWA A W WIDE POSLEDOWATELXNOSTI, ZAPISAW SNA- ^ALA \LEMENT, SOOTWETSTWU@]IJ ^ISLU 1, ZATEM \LEMENT, SOOTWET- STWU@]IJ ^ISLU 2, I T.D.

nAOBOROT, ESLI WSE \LEMENTY MNOVESTWA A ZAPISANY W WIDE PO- SLEDOWATELXNOSTI (1.8.1), TO POSTAWIW \LEMENT ak W SOOTWETSTWIE ^ISLU k, POLU^IM WZAIMNO ODNOZNA^NOE SOOTWETSTWIE MNOVESTW A I

N.

s^ETNYE MNOVESTWA | SAMYE \MALENXKIE" SREDI BESKONE^NYH MNOVESTW. dEJSTWITELXNO, PUSTX MNOVESTWO A BESKONE^NO. wOZXMEM NEKOTORYJ \LEMENT IZ A, OBOZNA^AEM EGO a1. w SILU BESKONE^NOSTI A W A, KROME a1, ESTX E]E DRUGIE \LEMENTY. wYBIRAEM KAKOJ-LIBO IZ NIH I OBOZNA^AEM EGO a2. pRODOLVAQ NEOGRANI^ENNO \TOT PROCESS, POLU^IM S^ETNOE PODMNOVESTWO MNOVESTWA A. tAKIM OBRAZOM, KAV-

DOE BESKONE^NOE MNOVESTWO SODERVIT S^ETNOE PODMNOVESTWO. rASSMOTRIM PRIMERY S^ETNYH MNOVESTW.

pO^TI O^EWIDNYJ PRIMER | S^ETNOSTX MNOVESTWA Z. dEJSTWI- TELXNO, WSE CELYE ^ISLA MOVNO PREDSTAWITX W WIDE POSLEDOWATELX- NOSTI

0 1 ;1 2 ;2 : : : :

25

tEOREMA 1.8.1. mNOVESTWO RACIONALXNYH ^ISEL S^ETNO.

dOKAZATELXSTWO. tEOREMA BUDET DOKAZANA, ESLI MY POSTROIM PO- SLEDOWATELXNOSTX, SODERVA]U@ WSE RACIONALXNYE ^ISLA (KAVDOE RACIONALXNOE ^ISLO DOLVNO U^ASTWOWATX W \TOJ POSLEDOWATELXNOS- TI TOLXKO ODIN RAZ). dLQ \TOGO STROIM SNA^ALA POSLEDOWATELXNOSTI, SODERVA]IE WSE OTLI^NYE OT NULQ RACIONALXNYE ^ISLA S FIKSIRO- WANNYMI ZNAMENATELQMI:

1	1	2	2	. . . .
1	1	1	1
1	1	2	2	. . . .
2	2	2	2
1	1	2	2	. . . .
3	3	3	3
. . .	. . .	. . .	. . .	. . . .

tEPERX PI[EM ^ISLO 0, A ZATEM ZAPISYWAEM ^ISLA, DWIGAQSX W POSTROENNOJ BESKONE^NOJ TABLICE PO DIAGONALQM. pERED TEM, KAK NAPISATX O^EREDNOE ^ISLO, PROWERQEM, ^TO \TOGO ^ISLA NET SREDI UVE ZAPISANNYH.

tAK POLU^IM NUVNU@ POSLEDOWATELXNOSTX.

tEOREMA 1.8.2. mNOVESTWO DEJSTWITELXNYH ^ISEL NES^ETNO.

dOKAZATELXSTWO. pOKAVEM, ^TO NES^ETNO MNOVESTWO DEJSTWITELX- NYH ^ISEL IZ INTERWALA (0 1).

pREDPOLOVIM, ^TO \TO UTWERVDENIE NEWERNO I SU]ESTWUET PO-

SLEDOWATELXNOSTX
x1 x2 x3 : : :	(1.8.2)
SODERVA]AQ WSE ^ISLA IZ (0 1). pUSTX xn	= 0 xn1xn2 : : : , n =

= 1 2 : : : | PREDSTAWLENIE ^ISEL xn W WIDE BESKONE^NYH DESQTI^- NYH DROBEJ. mY S^ITAEM, ^TO WYBRANA KAKAQ-LIBO ODNA FORMA ZA- PISI BESKONE^NYH DESQTI^NYH DROBEJ | ILI S 0, ILI S 9 W PERIODE. zAPI[EM \TI PREDSTAWLENIQ W WIDE BESKONE^NOJ TABLICY:

x1 = 0 x11x12x13 : : :

x2 = 0 x21x22x23 : : :

x3 = 0 x31x32x33 : : :

: : : : : : : : : : : :

26

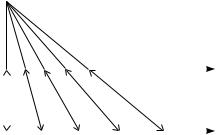
pOSTROIM ^ISLO IZ INTERWALA (0 1), KOTOROGO W POSLEDOWATELX- NOSTI (1.8.2) NET.

pOLOVIM a := 0 a1a2 : : : , GDE WSE DESQTI^NYE ZNAKI ai WYBI-

RAEM SREDI CIFR 1 2	: : : 8 TAK, ^TOBY WYPOLNQLISX NERAWENSTWA
a1 6= x11 a2 6= x22 : : : .	tOGDA W ZAPISI ^ISLA	a	W WIDE BESKONE^NOJ

DESQTI^NOJ DROBI CIFRY 0 I 9 NE U^ASTWU@T WOWSE, I ^ISLO a NE MOVET RAWNQTXSQ NI ODNOMU IZ ^ISEL xn, TAK KAK an =6 xnn DLQ WSEH n. tEOREMA DOKAZANA.

oPREDELENIE. mNOVESTWA, IME@]IE ODINAKOWU@ MO]NOSTX S OT- REZKOM [0 1], NAZYWA@T MNOVESTWAMI MO]NOSTI KONTINUUM.

w \TOM OPREDELENII MOVNO BYLO GOWORITX OB ODINAKOWOJ MO]- NOSTI S INTERWALOM (0 1), TAK KAK NETRUDNO USTANOWITX WZAIMNO ODNOZNA^NOE SOOTWETSTWIE OTREZKA [0 1] I INTERWALA (0 1).

|TO MOVNO SDELATX, NAPRIMER, TAK. wYDELIM PROIZWOLXNOE S^ET- NOE MNOVESTWO A (0 1). zAPI[EM WSE \LEMENTY A W WIDE PO- SLEDOWATELXNOSTI a1 a2 : : : (WSE \LEMENTY \TOJ POSLEDOWATELXNOS- TI RAZLI^NY) I RASSMOTRIM POSLEDOWATELXNOSTX B, IME@]U@ WID

0 1 a1 a2 : : : .

wSEM ^ISLAM IZ (0 1), NE WHODQ]IM W A, STAWIM W SOOTWETSTWIE IH SAMIH KAK \LEMENTY IZ [0 1]. a POSLEDOWATELXNOSTI A I B ZAPI- SYWAEM ODNU POD DRUGOJ

a1 a2 a3 a4 : : : 0 1 a1 a2 : : :

I STAWIM W SOOTWETSTWIE DRUG DRUGU \LEMENTY IZ ODNOGO STOLBCA. w OPREDELENII MNOVESTW MO]NOSTI KONTINUUM NE IMEET ZNA^E- NIQ I TOT FAKT, ^TO BERETSQ IMENNO OTREZOK [0 1]. mOVNO BYLO BRATX L@BOJ OTREZOK [a b], TAK KAK WZAIMNO ODNOZNA^NOE SOOTWET-

STWIE MEVDU [0 1] I [a b]		LEGKO USTANOWITX S POMO]X@ FORMULY
t = a + (b ; a)x x 2 [0 1], ILI GEOMETRI^ESKI:
0		1	x
a		b	t

w DALXNEJ[EM MY UWIDIM, ^TO MNOVESTWO WSEH DEJSTWITELXNYH ^ISEL TAKVE IMEET MO]NOSTX KONTINUUM.

27

gLAWA 2

predel posledowatelxnosti

x 2.1. oPREDELENIE PREDELA POSLEDOWATELXNOSTI

nAPOMNIM OPREDELENIE POSLEDOWATELXNOSTI \LEMENTOW PROIZ- WOLXNOGO MNOVESTWA A, DANNOE W x1.7. eSLI KAVDOMU NATURALXNOMU ^ISLU n POSTAWLEN W SOOTWETSTWIE NEKOTORYJ \LEMENT xn IZ MNO- VESTWA A, TO GOWORQT, ^TO \LEMENTY

x1 x2 x3 : : :

OBRAZU@T POSLEDOWATELXNOSTX fxng.

w \TOJ GLAWE W OSNOWNOM RASSMATRIWA@TSQ ^ISLOWYE POSLEDO- WATELXNOSTI. dLQ KRATKOSTI BUDEM NAZYWATX IH PROSTO POSLEDOWA- TELXNOSTQMI.

oPREDELENIE. ~ISLO a NAZYWA@T PREDELOM POSLEDOWATELXNOSTI fxng, ESLI DLQ KAVDOGO POLOVITELXNOGO " SU]ESTWUET ^ISLO N = N(") TAKOE, ^TO DLQ WSEH n > N WYPOLNQETSQ NERAWENSTWO

jxn ; aj < ":		(2.1.1)
w \TOM SLU^AE PI[UT
a = lim xn = lim xn = lim xn		(2.1.2)
n!1	n
ILI
xn ! a	n ! 1:

pRI a = 0 \TO OPREDELENIE BYLO DANO W x1.7, KOGDA GOWORILOSX O POSLEDOWATELXNOSTQH, SHODQ]IHSQ K NUL@.

nERAWENSTWO (2.1.1) RAWNOSILXNO DWOJNOMU NERAWENSTWU ;" < xn ; a < " I, ZNA^IT, RAWNOSILXNO DWOJNOMU NERAWENSTWU a ; " < xn < a + ", KOTOROE OZNA^AET, ^TO

xn 2 (a ; " a + "):

oPREDELENIE. iNTERWAL (a ; " a + "), GDE " > 0, NAZYWA@T

"-OKRESTNOSTX@ TO^KI a.

iSPOLXZUQ PONQTIE "-OKRESTNOSTI, OPREDELENIE PREDELA MOVNO SFORMULIROWATX TAK. ~ISLO a NAZYWAETSQ PREDELOM POSLEDOWATELX- NOSTI, ESLI DLQ KAVDOGO POLOVITELXNOGO ^ISLA " WSE ^LENY POSLE- DOWATELXNOSTI, NA^INAQ S NEKOTOROGO, PRINADLEVAT "-OKRESTNOSTI TO^KI a.

28

oPREDELENIE. eSLI POSLEDOWATELXNOSTX IMEET PREDEL, EE NAZYWA- @T SHODQ]EJSQ. eSLI POSLEDOWATELXNOSTX NE IMEET PREDELA, EE NA-

ZYWA@T RASHODQ]EJSQ.

eSLI ^ISLO a QWLQETSQ PREDELOM POSLEDOWATELXNOSTI fxng, TO GOWORQT, ^TO POSLEDOWATELXNOSTX SHODITSQ K a. pRO ^LENY POSLEDO- WATELXNOSTI (^ISLA xn) GOWORQT, ^TO ONI SHODQTSQ ILI STREMQTSQ K a.

oTMETIM, ^TO SHODIMOSTX ILI RASHODIMOSTX POSLEDOWATELXNOS- TI I ZNA^ENIE PREDELA, ESLI POSLEDOWATELXNOSTX SHODITSQ, NE ZAWI- SQT OT EE NA^ALXNYH ^LENOW.

tEOREMA 2.1.1. pREDEL SHODQ]EJSQ POSLEDOWATELXNOSTI OPREDELQETSQ ODNOZNA^NO.

dOKAZATELXSTWO. pREDPOLOVIM PROTIWNOE | PUSTX ^ISLA a I b QWLQ@TSQ PREDELAMI POSLEDOWATELXNOSTI fxng I a 6= b, DLQ OPREDE- LENNOSTI a < b. wOZXMEM " := (b ; a)=2. |TO ^ISLO POLOVITELXNOE. pOLXZUQSX SHODIMOSTX@ POSLEDOWATELXNOSTI K a, NAHODIM N1 TA-

KOE, ^TO

a ; " < xn < a + "

(2.1.3)

DLQ WSEH n > N1. tO^NO TAKVE W SILU SHODIMOSTI POSLEDOWATELX- NOSTI K b NAHODIM N2 TAKOE, ^TO

b ; " < xn < b + "

(2.1.4)

DLQ WSEH n > N2. pO\TOMU, ESLI n > N := max(N1 N2), TO WYPOL- NQ@TSQ OBA NERAWENSTWA: I (2.1.3) I (2.1.4). tAK KAK

a + " = a + b ; a = a + b 2 2

I b ; " = (a + b)=2, TO IZ PRAWOGO NERAWENSTWA (2.1.3) I LEWOGO NERA- WENSTWA (2.1.4) SLEDUET, ^TO DLQ n > N

xn < a + " =	a + b	= b ; " < xn
	2

I MY PRI[LI K PROTIWORE^I@. tEOREMA DOKAZANA.

pRI DOKAZATELXSTWE TEOREMY RASSMATRIWALISX NERAWENSTWA (2.1.3) I (2.1.4), KOTORYE IMELI MESTO PERWOE DLQ n > N1 I WTOROE DLQ n > N2. ~TOBY WYPOLNQLISX OBA \TI NERAWENSTWA, MY BRALI n > N = max(N1 N2). tAKOJ PRIEM BUDET ^ASTO ISPOLXZOWATXSQ W DALXNEJ[EM BEZ DOPOLNITELXNYH POQSNENIJ.

29

x 2.2. sWOJSTWA PREDELOW, SWQZANNYE S NERAWENSTWAMI

tEOREMA 2.2.1. eSLI POSLEDOWATELXNOSTX SHODITSQ, TO ONA OGRANI^ENA.

dOKAZATELXSTWO. pUSTX POSLEDOWATELXNOSTX fxng SHODITSQ I a :=

lim xn. wZQW " = 1, NAHODIM N TAKOE, ^TO DLQ WSEH n > N WYPOLNQ-

n

ETSQ NERAWENSTWO jxn ; aj < 1. tOGDA DLQ \TIH n

jxnj = jxn ; a + aj 6 jxn ; aj + jaj < 1 + jaj:

pO\TOMU, ESLI POLOVITX L := max(jx1j jx2j : : : jxN j 1 + jaj), TO PO- LU^IM jxnj 6 L DLQ WSEH n, T.E. POSLEDOWATELXNOSTX fxng OGRANI^E-

NA.

tEOREMA 2.2.2. eSLI lim xn	= a = 0, TO SU]ESTWUET ^ISLO N
n	6
TAKOE, ^TO DLQ WSEH n > N
	1
jxnj > 2 jaj:
pRI \TOM, ESLI a > 0, TO xn > a=2, A ESLI a < 0, TO xn < a=2.
dOKAZATELXSTWO. wZQW " :=	jaj=2, NAJDEM N TAKOE, ^TO DLQ WSEH
n > N WYPOLNQETSQ NERAWENSTWO
	1
jxn ; aj < 2 jaj:
tOGDA
1		1
a ; 2 jaj < xn < a +		2 jaj:	(2.2.1)

eSLI a > 0, TO jaj = a I POLXZUEMSQ LEWYM NERAWENSTWOM (2.2.1). a ESLI a < 0, TO jaj = ;a I POLXZUEMSQ PRAWYM NERAWENSTWOM (2.2.1).

tEOREMA DOKAZANA.

tEOREMA 2.2.3. eSLI POSLEDOWATELXNOSTI fxng I fyng SHODQTSQ I xn 6 yn DLQ WSEH n, TO

lim xn 6 lim yn:

n!1 n!1

dOKAZATELXSTWO. pUSTX a := lim xn I b := lim yn. nUVNO DOKAZATX, ^TO a 6 b.

30