9.2 Регрессионный анализ. Множественная регрессия

Линейная модель множественной регрессии имеет вид:

Y i = 0 + 1x i 1 +2x i 2 +…+ m x i m + i , (9.1.)

коэффициент регрессии j показывает, на какую величину в среднем изменится результативный признак Y, если переменную xj увеличить на единицу измерения, т. е. j является нормативным коэффициентом. Обычно предполагается, что случайная величина i имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией .

Анализ уравнения (9.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (9.2.):

Y = X  + , (9.2.)

Y – это вектор зависимой переменной размерности п  1, представляющий собой п наблюдений значений уi, Х— матрица п наблюдений независимых переменных X1, X 2, X 3 , … X m, размерность матрицы Х равна п  (т+1); — подлежащий оцениванию вектор неизвестных параметров размерности (т+1)  1; — вектор случайных отклонений (возмущений) размерности п  1. Таким образом,

Y = ,X = , =

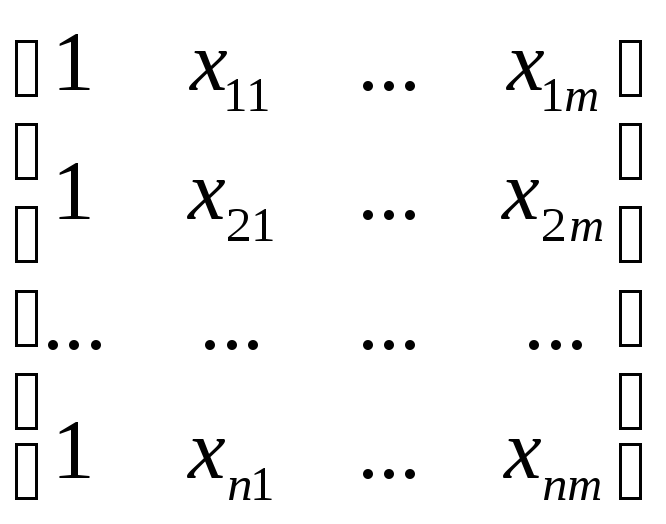Уравнение (9.1) содержит значения неизвестных пара­метров 0,1,2,… ,m. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрес­сии, в которой вместо истинных значений параметров под­ставлены их оценки (а именно такие регрессии и приме­няются на практике), имеет вид

Y =Ха + е=+е, (9.3)

где а — вектор оценок параметров; е — вектор «оценен­ных» отклонений регрессии, остатки регрессии е = Y - Ха; —оценка значе­ний Y, равная Ха.

Оценка параметров модели множественной регрессии с помощью метода наименьших квадратов.

Формулу для вычисления параметров регрессионного уравнения приведем без вывода

a = (X^т X )^-1 X ^т Y (9.4).

Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т. е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы ис­ходных данных линейно независимы. Для экономических показате­лей это условие выполняется не всегда. Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисле­ние параметров либо невозможным, либо затрудняет содержатель­ную интерпретацию параметров модели. Мультиколлинеарность может возникать в силу разных причин. На­пример, несколько независимых переменных могут иметь общий вре­менной тренд, относительно которого они совершают малые колебания. В частности, так может случиться, когда значения одной независимой переменной являются лагированными значениями другой. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0.8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени свя­зан с зависимой переменной.

В качестве крите­рия мультиколлинеарности может быть принято соблюдение следующих неравенств:

r_yxi > r_xixk , r_yxk > r_xixk , r_xixk < 0.8

Если приведенные неравенства (или хотя бы одно из них) не выполняются, то в модель включают тот фактор, который наиболее тесно связан с Y.

Оценка качества модели регрессии.

Качество модели регрессии оценивается по следующим направлениям:

1. проверка качества всего уравнения регрессии;

2. проверка значимости всего уравнения регрессии;

3. проверка статистической значимости коэффициентов уравнения регрессии;

4. проверка выполнения предпосылок МНК.

Для оценки качества модели множественной регрессии вычисляют коэффициент множественной корреляции (индекс корреляции) R и коэффициент детерминации R2. Чем ближе к 1 значение этих характеристик, тем выше качество модели.

В многофакторной регрессии добавление дополнительных объ­ясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скор­ректирован с учетом числа независимых переменных. Скоррек­тированный R2, или , рассчитывается так:

, (9.5)

где n — число наблюдений;

k — число независимых переменных.

Проверка значимости модели регрессии

Для проверки значимости модели регрессии используется F-критерий Фишера, вычисляемый по формуле:

(9.6)

Если расчетное значение с 1= k и 2 = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

Анализ статистической значимости параметров модели

Значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

t_aj = /S_aj , (9.7.)

где _Saj — это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj. Величина Saj представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии иj -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.

S_aj = ,(9.8)

где b_jj - диагональный элемент матрицы (Х^Т Х)^-1.

Если расчетное значение t-критерия с (n - k - 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели, при этом оставшиеся в модели параметры должны быть пересчитаны.

Проверка выполнения предпосылок МНК.

Проверка выполнения предпосылок МНК выполняется на основе анализа остаточной компоненты.

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины. В классических методах регрессионного анализа предполагается также нормальный закон распределения остатков.

Исследование остатков полезно начинать с изучения их графика. 0н может показать наличие какой-то зависимости, не учтенной в модели. Скажем, при подборе простой линейной зависимости между Y и X график остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной) или включения в модель пе

График остатков хорошо показывает и резко отклоня­ющиеся от модели наблюдения — выбросы. Подобным аномальным наб риодических компонент.людениям надо уделять особо пристальное внимание, так как их присутствие мо­жет грубо искажать значения оценок. Устранение эффектов вы­бросов может проводиться либо с помощью удаления этих точек из анализируемых данных, (эта процедура называется цензурированием), либо с помощью применения методов оценивания параметров, устойчи­вых к подобным грубым отклонениям.

Независимость остатков проверяется с помощью критерия Дарбина – Уотсона.

Корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько шагов, называется автокорреляцией.

Автокорреляция случайной составляющей нарушает одну из предпосылок нормальной линейной модели регрессии.

Наличие (отсутствие) автокорреляции в отклонениях проверяют с помощью критерия Дарбина – Уотсона. Численное значение коэффициента равно

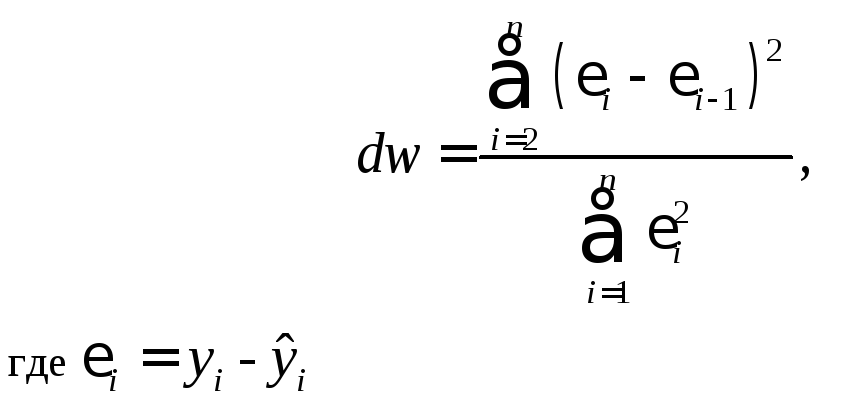(9.9)

Значение dw статистики близко к величине 2(1–r(1)), где r(1) - выборочная автокорреляционная функция остатков первого порядка. Таким образом, значение статистики Дарбина - Уотсона распределено в интервале от 0 до 4. Соответственно, идеальное значение статистики - 2 (автокорреляция отсутствует). Меньшие значения критерия соответствуют положительной автокорреляции остатков, большие значения - отрицательной. Статистика учитывает только автокорреляцию первого порядка. Оценки, получаемые по критерию, являются не точечными, а интервальными. Верхние (d2) и нижние (d1) критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции, зависят от количества уровней динамического ряда и числа независимых переменных модели. Значения этих границ для уровня значимости = 0,05 даны в специальных таблицах (Приложение 9.1).