Контрольные вопросы

1. Понятия случайный вектор, случайные одномерные величины,

к-мерная случайная величина.

2. Функция распределения случайного вектора, его свойства.

3. Плотность и функция распределения непрерывной к-мерной случайной величины, их свойства.

4. Вероятность попадания дискретной к-мерной случайной величины в любую точку счетного множества допустимых точек.

5. Функция распределения дискретной к-мерной случайной величины.

6. Плотность вероятностей двумерного нормального распределения зависимых и независимых случайных величин.

7. Условное нормальное распределение. Центр распределения и дисперсия, линия нормальной регрессии.

8. Неравенство Чебышева.

9. Теорема Бернулли.

10. Закон больших чисел.

Лекция 6

Оценивание параметров. Статистическая проверка гипотез

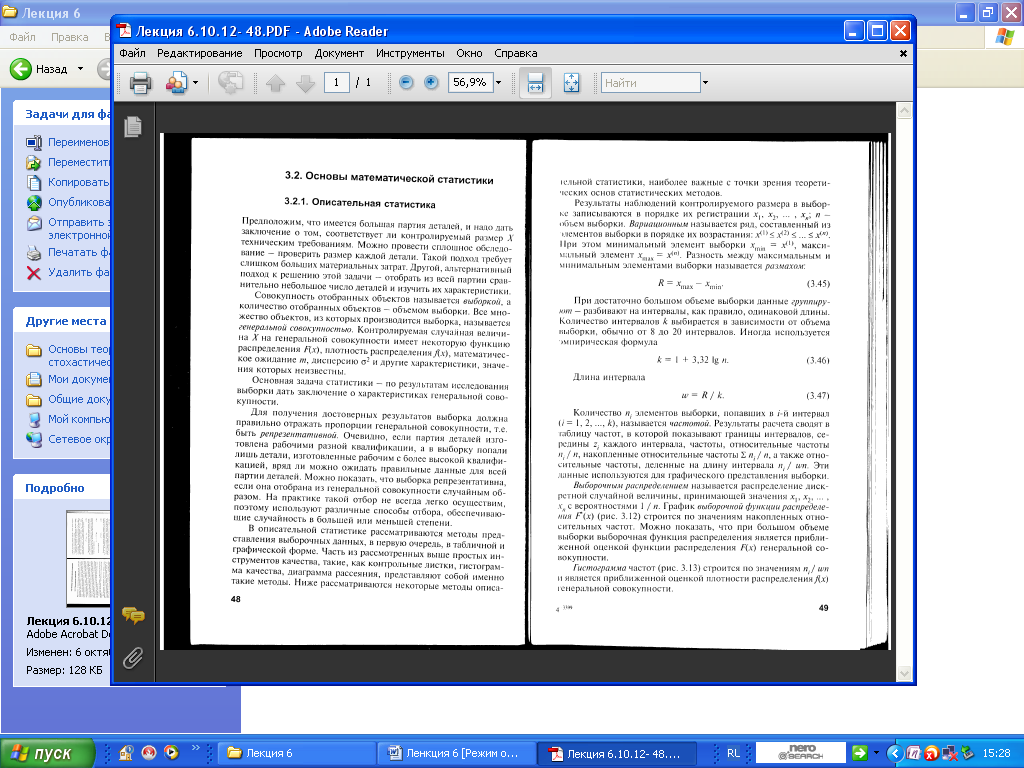
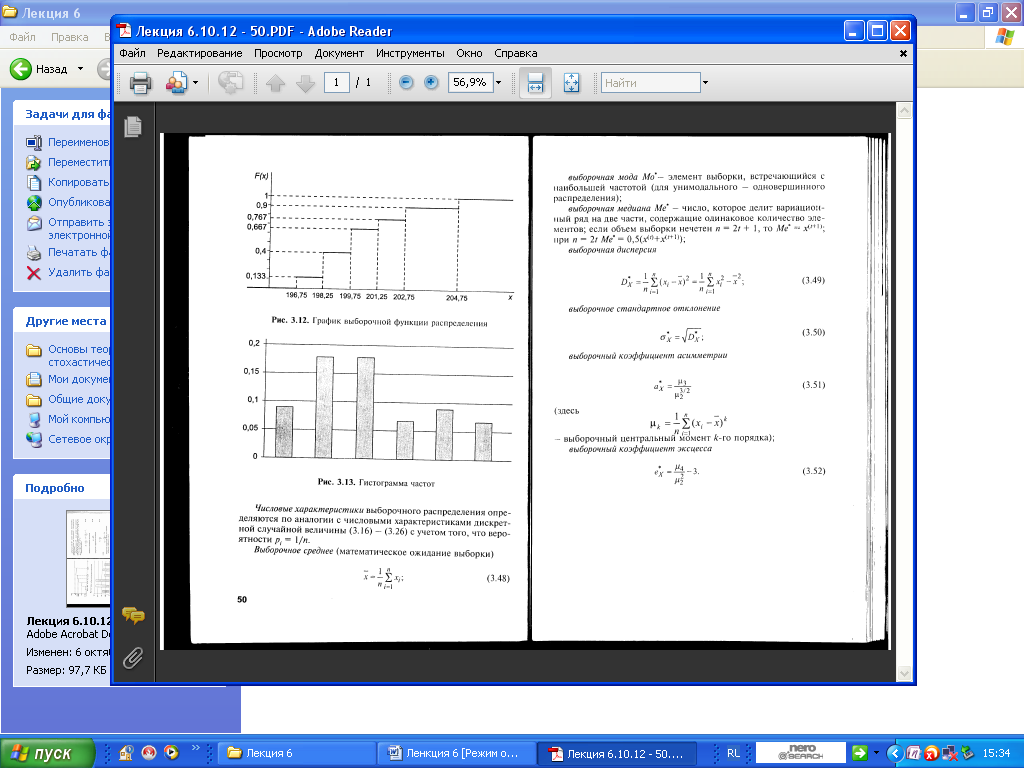
6.1. Описательная статистика

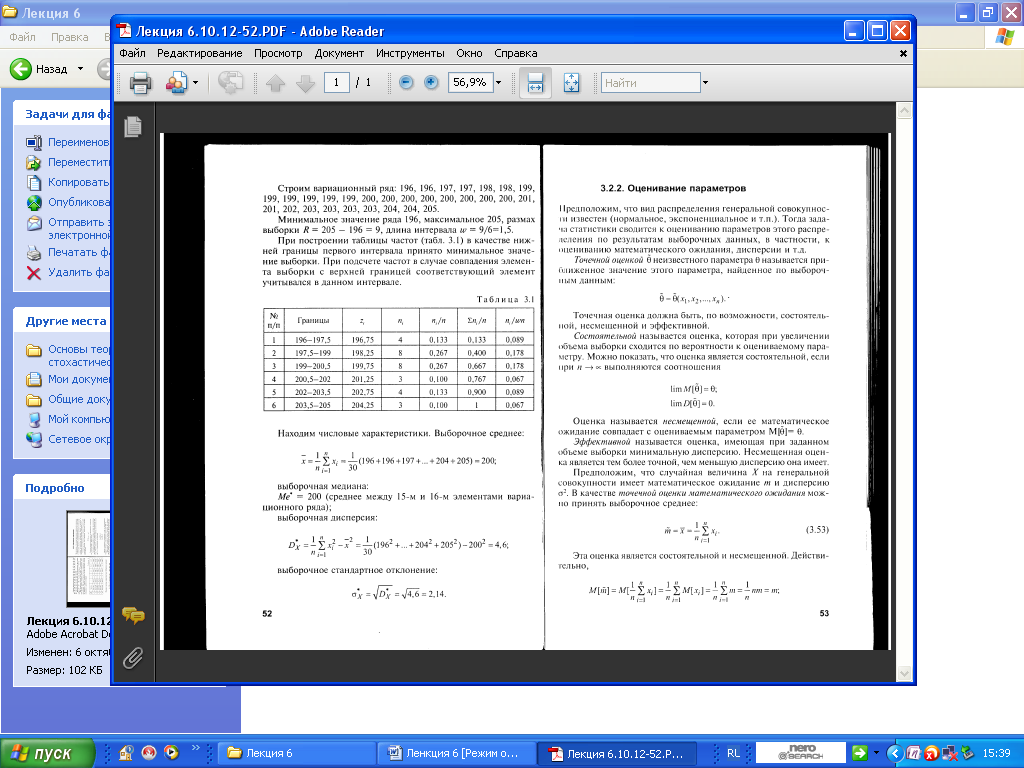
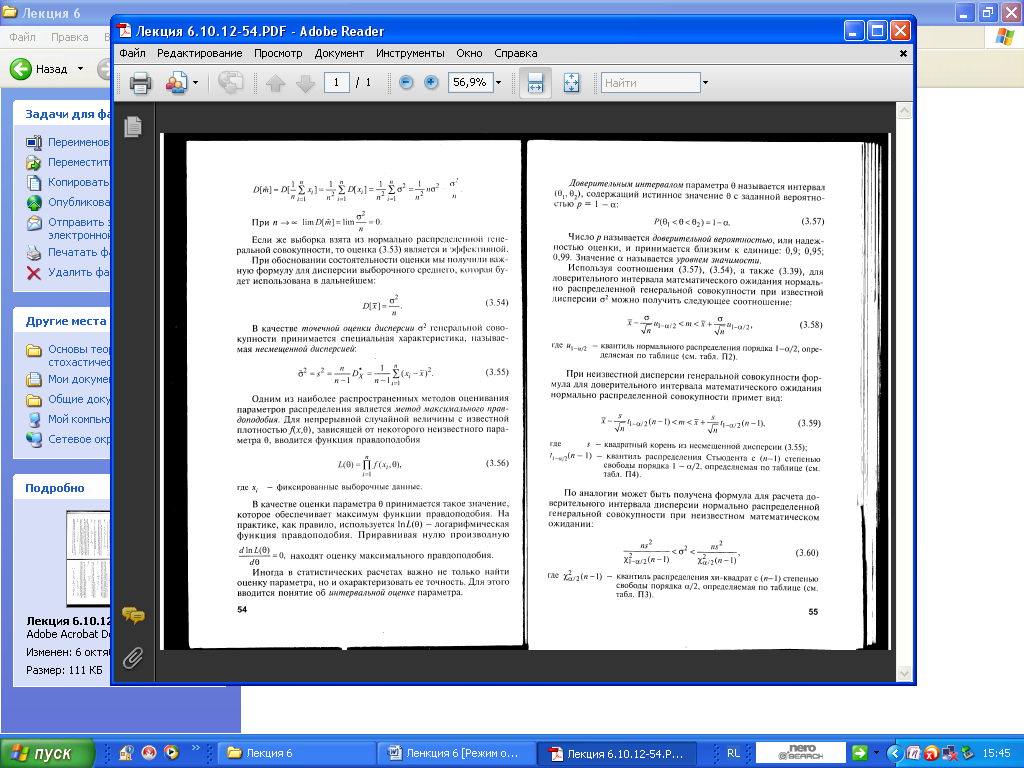
6.2. Оценивание параметров

6.3.

6.4.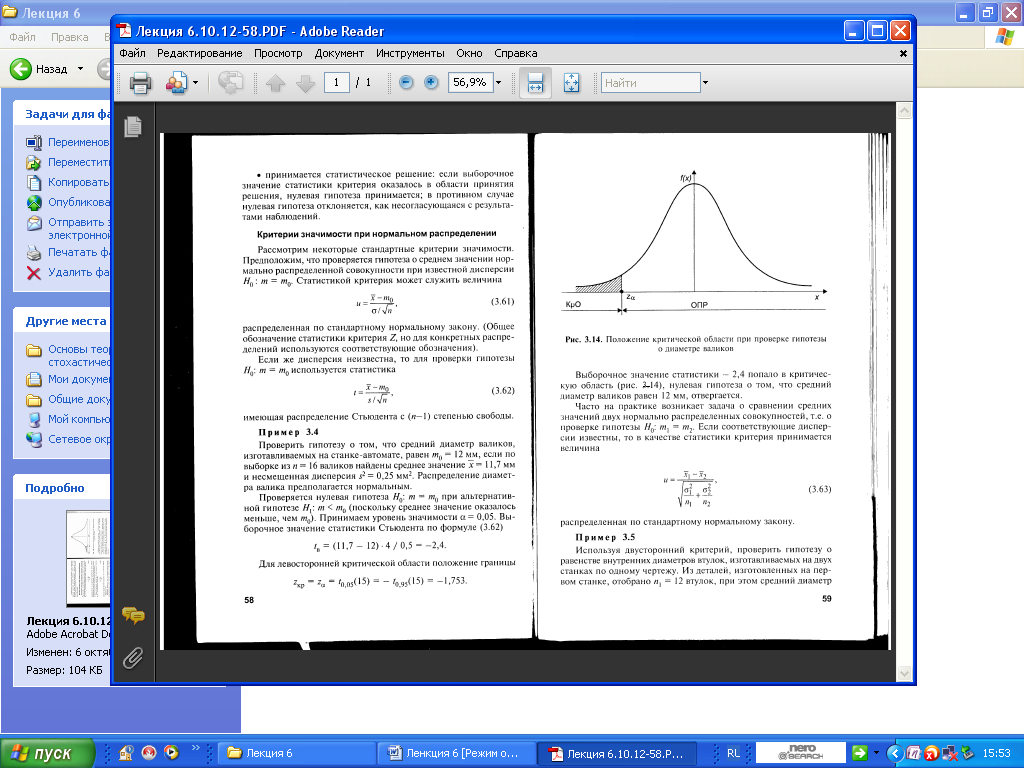

6.5.

6.6.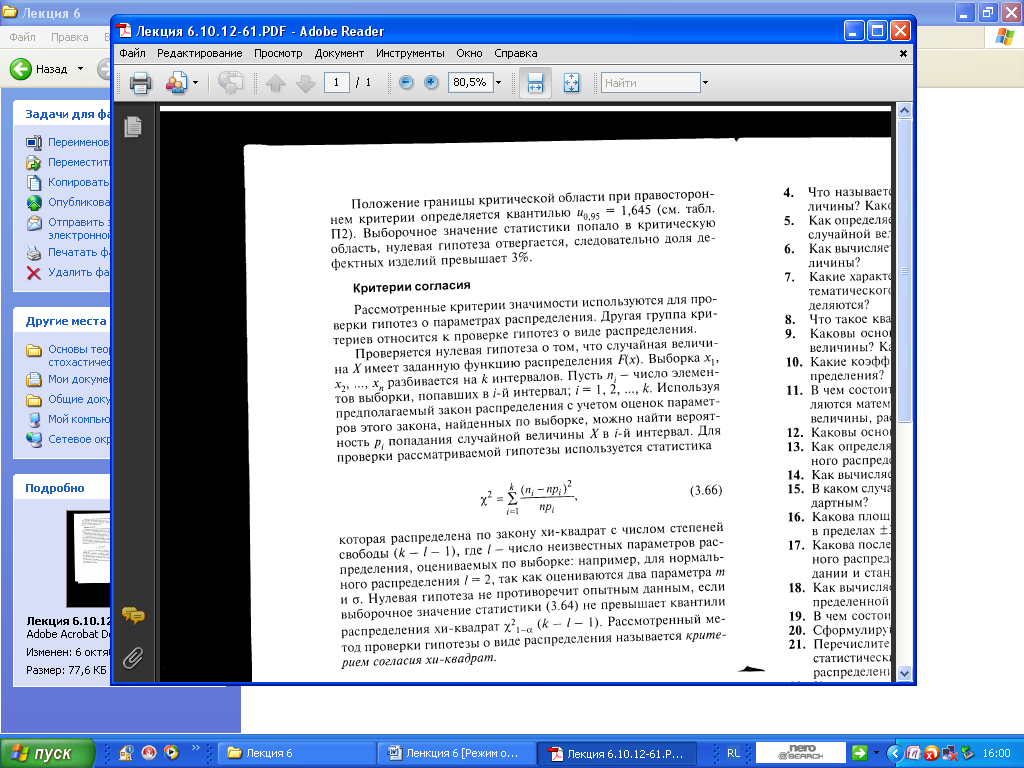

Контрольные вопросы

1. Что рассматриваются в описательной статистике?

2. Что называется вариационным рядом и как он составляется?

3. Как группируются выборки большого объема?

4. Как строиться выборочная функция распределения?

5. Как строится гистограмма частот?

5. Как вычисляются числовые характеристики выборочного распределения?

6. Что называется точечной оценкой неизвестного параметра?

7. Понятие состоятельности, несмещенности и эффективности оценок.

8. Сущность метода максимального правдоподобия, используемого для оценивания параметров распределения.

9.Что называется доверительным интервалом параметра и доверительной вероятностью?

10. Как вычисляется доверительный интервал математического ожидания нормального распределения?

11. Как вычисляется доверительный интервал дисперсии нормального распределения?

Лекция 7Случайные процессы и их аналитическое описание

7.1

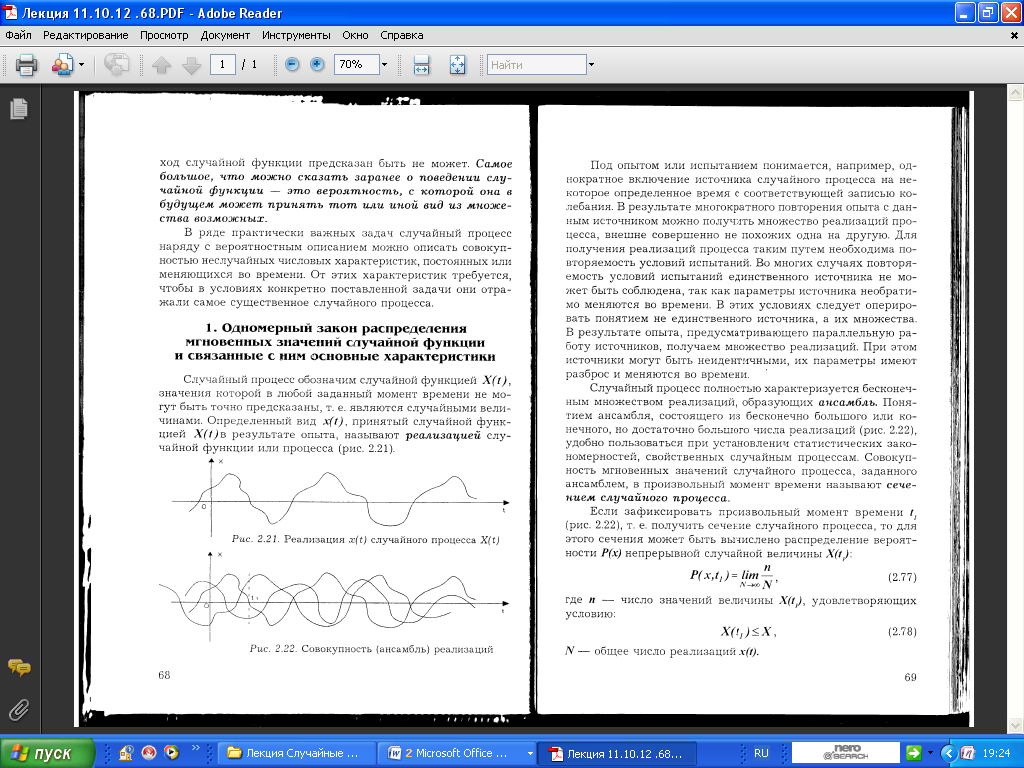
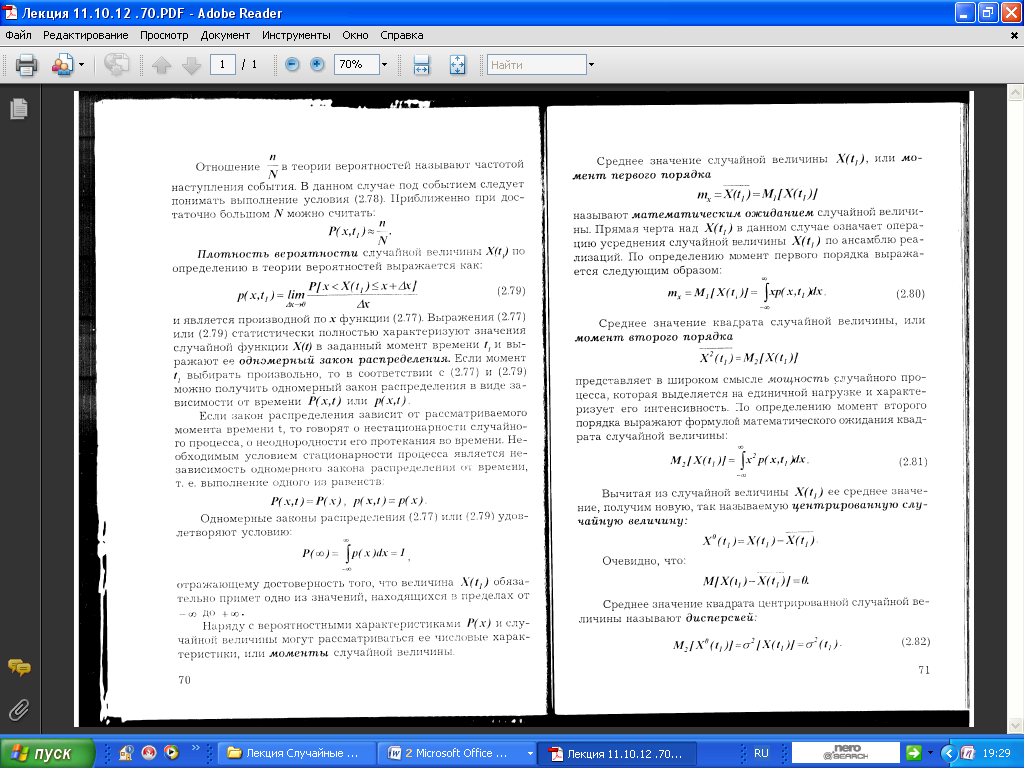
7.2

7.3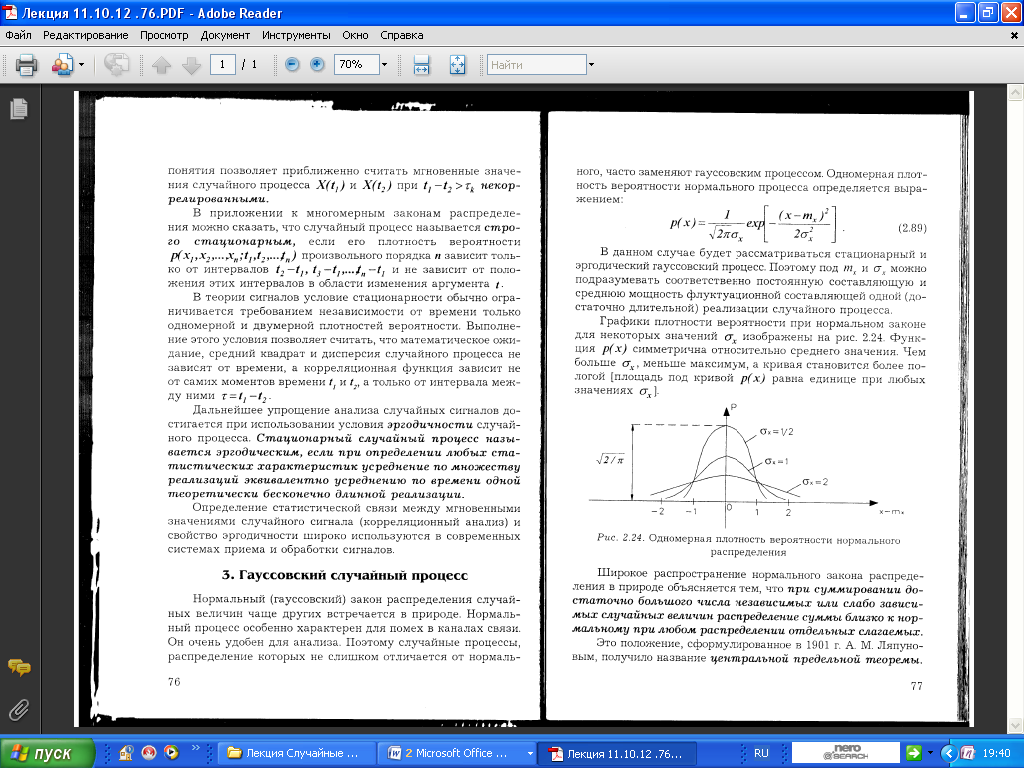

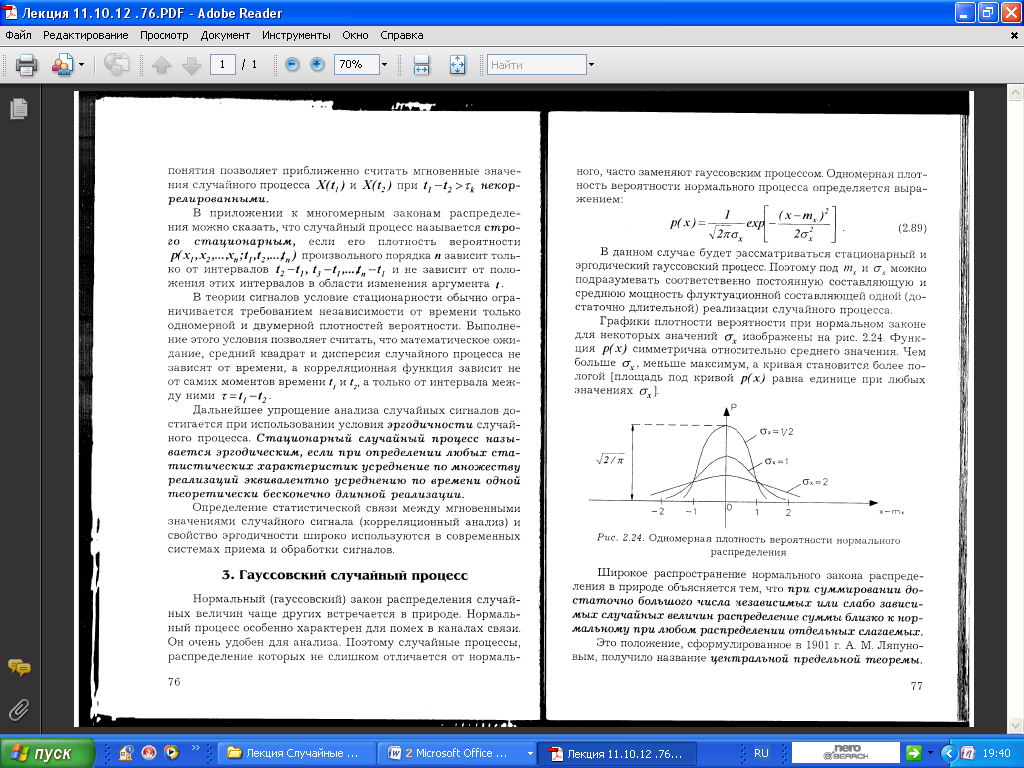
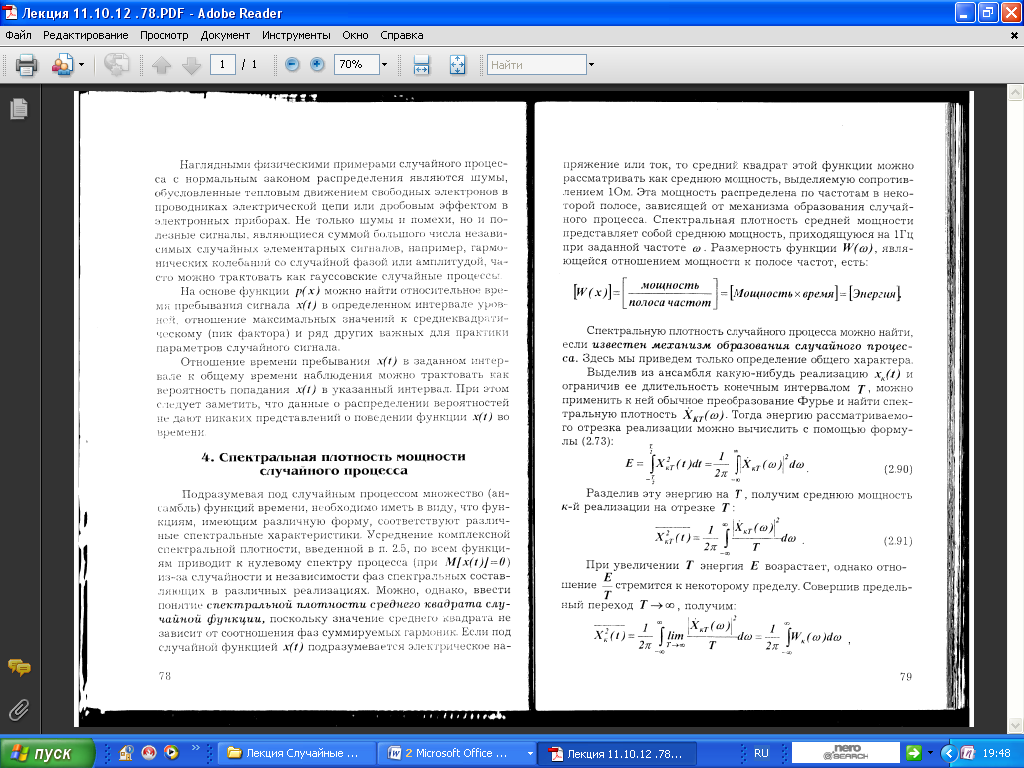
7.4 Определение статистических оценок математического ожидания и корреляционной функции случайного процесса

Рассмотрим случайный процесс как совокупность величин X(t). Мы можем в отношении каждой из них решать статистическую оценку интересующих нас параметров: математических ожиданий M[X(t)] и корреляционных моментов R_X(t₁, t₂), Для этого необходимо располагать достаточным числом независимых реализаций процесса X(t), полученных в одинаковых условиях (например, осциллограммы). Для всех реализаций выбирается общее начало отсчета по параметру t, например, начало цикла по изучаемому процессу.

Далее ось параметров разбивается на k равных интервалов, выбирая их длину так, чтобы на ее протяжении каждая реализация мало изменялась. При каждом значении t_i в конце каждого интервала математическое ожидание M[X(t_i)] мы оцениваем по средней арифметической x^cp(t_i) из значений x_i,1, x_{i,2, ….}x_i,n величины полученных из n реализаций процесса.

Получив ряд средних арифметических x^cp(t₁), x^cp(t₂), … x^cp(t_k), их аппроксимируют подходящей кривой и, таким образом получают эмпирическую оценку x^cp(t), функции M[X(t)] – математического ожидания процесса.

При оценке корреляционного момента пользуются выше описанной методикой, формула для вычислений имеет вид:

R_X ^cp(t₁, t₂) = 1/n[x_l(t₁) – x^cp(t₁)][x_l(t₂) – x^cp(t₂)]

где n – число реализаций; t₁, t₂ выборочные параметры t; l – реализация процесса 1, 2, .. n.

Давая t₁ и t₂ все возможные значения получают ряд значений R_X ^cp(t₁, t₂) Аппроксимируя эти значения подходящей поверхностью в координатной системе t₁, t₂, R_X(t₁, t₂) получают статистическую оценку корреляционной функции.

Аналогично определяют эмпирическое значение взаимной корреляционной функции двух случайных процессов X(t) и Y(t). Расчетная формула имеет вид:

R_XY ^cp(t₁, t₂) = 1/n [x_l(t₁) – x^cp(t₁)][y_l(t₂) – y^cp(t₂)].