Приклад №10

Довести, що різниця однакових степенів двох чисел завжди ділиться на різницю цих чисел, тобто при натуральному n .

Доведення

1) При n=1 твердження вірно:

.

2) Припустимо, що при n=k

Доведемо, що .

До виразу додамо два виразиі -. Одержимо

.

Перший доданок одержаної суми ділиться на , тому що другий ділиться наза припущенням.

Отже, і вся сума тоді ділиться на

За припущенням математичної індукції

при будь-якому n.

При доведенні деяких тверджень, які запропоновують на різних математичних олімпіадах, теж корисно застосовувати метод повної математичної індукції.

Наведемо приклади таких завдань (№11, №12).

Приклад №11

Довести, що ділиться на (1+2+...+m), де n, mєN і n – непарне.

Доведення.

Введемо позначення

. Тоді подвоєну цю суму можна записати так:

Оскільки n – непарне, то кожний додаток ділиться на (m+1) за наслідком з теореми Безу, тому . Тоді в силу довільності m, 2S_m-1m. Дійсно,

.

Але найбільший спільний дільник НСД(m;m+1)=1, то , q – натуральне число.

З іншого боку,

(ця формула доведена методом математичної індукції)

тому , що і треба було довести.

Приклад №12

Нехай a₁, a₂, a₃, …, a_n – послідовність чисел, утворених за таким законом:

a₁=1, a_n=na_n-1+(-1)ⁿ. Довести, що при n>1 a_n ділиться на n-1.

Доведення.

1) Базис індукції. Якщо n=2, то твердження справджується:

a₂=21+(-1)²=2+1=3(2-1).

2) Припустимо, що n>2.

Тоді: a_n= na_n-1+(-1)ⁿ,

a_n-1=(n-1)a_n-2+(-1)^n-1.

Додавши ці дві рівності, одержимо

a_n+a_n-1=na_n-1+(-1)ⁿ+(n-1)a_n-2+(-1)^n-1.

a_n=na_n-1-a_n-1+(n-1)a_n-2.

a_n=(n-1)a_n-1+(n-1)a_n-2=(n-1)(a_n-1+a_n-2).

(n-1)(a_n-1+a_n-2) (n-1) за принципом математичної індукції.

Отже, a_n(n-1) при, n>1.

Доведення деяких рівностей і тотожностей

методом математичної індукції

Приклад №1

Довести методом математичної індукції, що для nєN

.

Доведення

1) Перевіримо, чи справджується ця формула при n=1:

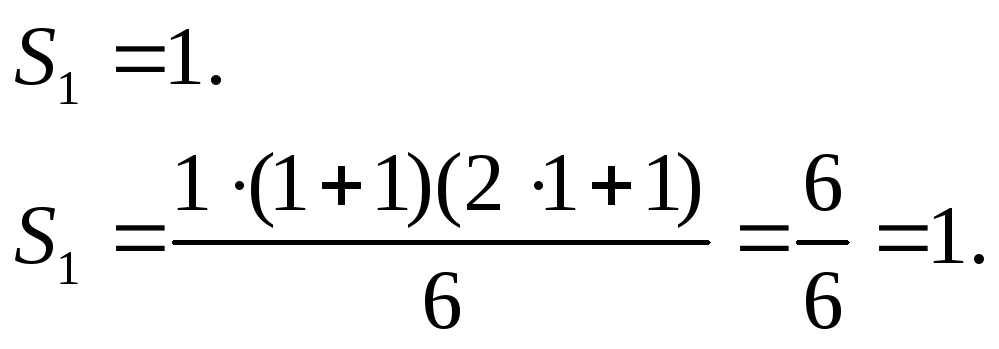
Так, формула справджується.

2) Припустимо, що формула справджується при n=k, тобто

(*)

Доведемо справедливість формули при n=k+1. Тобто покажемо, що

З іншого боку

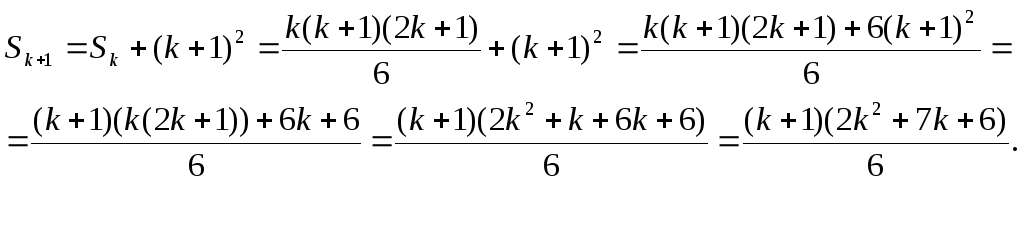
Розкладемо на множники тричлен

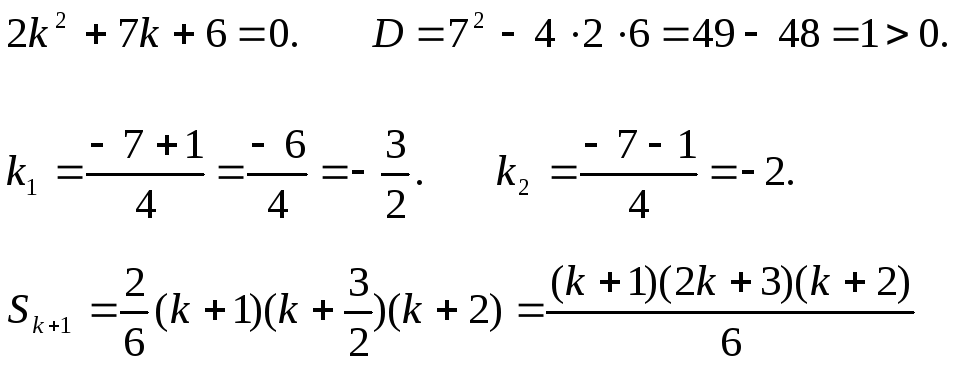
Отже, формула справджується при n=k+1. Тоді вона вірна і для будь-якого n натурального за принципом математичної індукції.

Приклад №2

Довести, що виконується рівність

при будь-якому натуральному n.

Доведення

1) При n=1

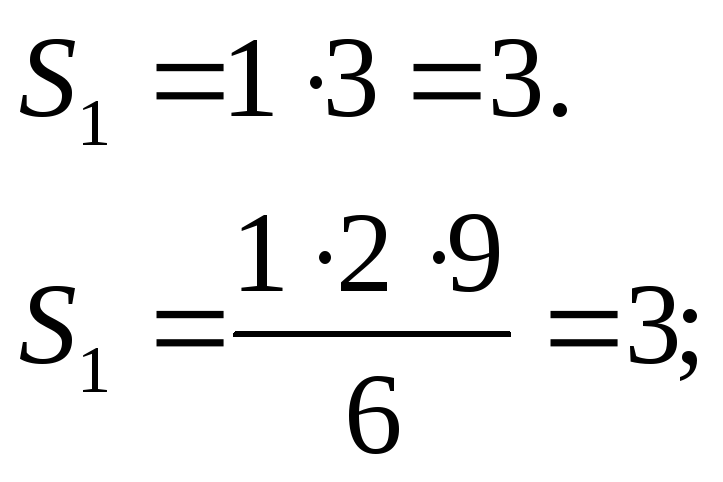
3=3 формула вірна.

2) Зробимо припущення, що дана формула справедлива і при n=k, тобто має місце рівність

Доведемо, що формула вірна і при n=k+1.

.

Враховуючи припущення, маємо

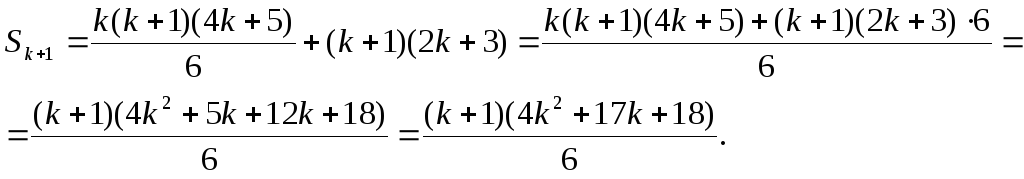
Розкладемо на множники тричлен :

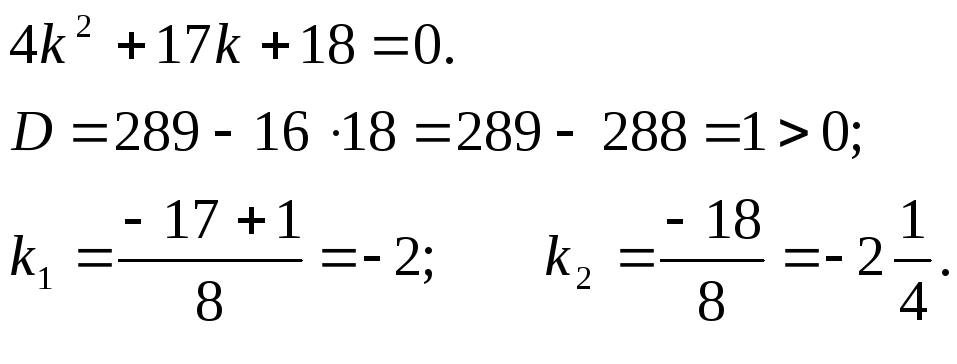
Отже

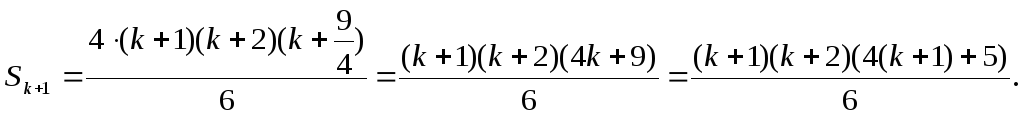
Формула вірна і при n=k+1.

За принципом математичної індукції вона вірна і при

Приклад №3

Довести, що для

Доведення

1) при n=1 S₁=5;

2) Нехай при n=k

Враховуючи це припущення, доведемо, що формула вірна і при n=k+1.

Формула вірна.

За припущенням математичної індукції вона справджується і для будь-якого натурального n.

Приклад №4

Довести, що при

.

Доведення

1) При n=1 формула вірна.

2) Припустимо, що формула вірна і при n=k, тобто

Враховуючи це припущення, доведемо, що вона вірна і при n=k+1.

Формула вірна. Тоді за принципом математичної індукції вона справджується і для будь-якого натурального n.

Приклад №5

Довести, що при

, де

Доведення

За методом математичної індукції маємо

1) при n=1

1=1 Формула вірна.

2) Припустимо, що при

Доведемо, що при

Отже, за принципом математичної індукції формула справджується для будь-якого натурального n.

Приклад №6

Довести, що

де

Доведення

1) Базис індукції.

При n=2 маємо

(у лівій частині) (у правій частині)

тобто при n=2 формула справедлива.

2) Індуктивний перехід

Припустимо, що формула вірна при n=k, kєN, k>2.

Доведемо, що формула справджується і при n=k+1.

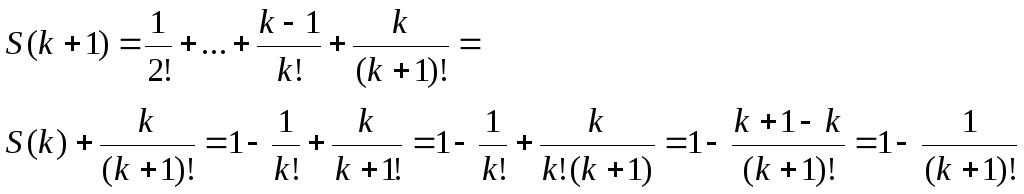
Формула справджується і при n=k+1. За принципом математичної індукції вона вірна і для будь-якого натурального

Приклад №7

Довести, що

.

Доведення

1) При n=1 маємо

Вірно!

2) Припустимо, що формула справджується при n=k, тобто має місце

Доведемо, що формула справедлива і при n=k+1, тобто, що

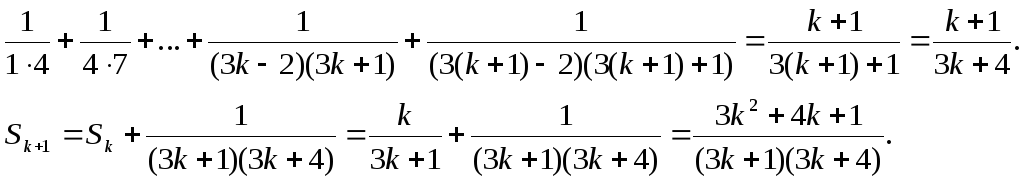
Розкладемо квадратний тричлен на множники:

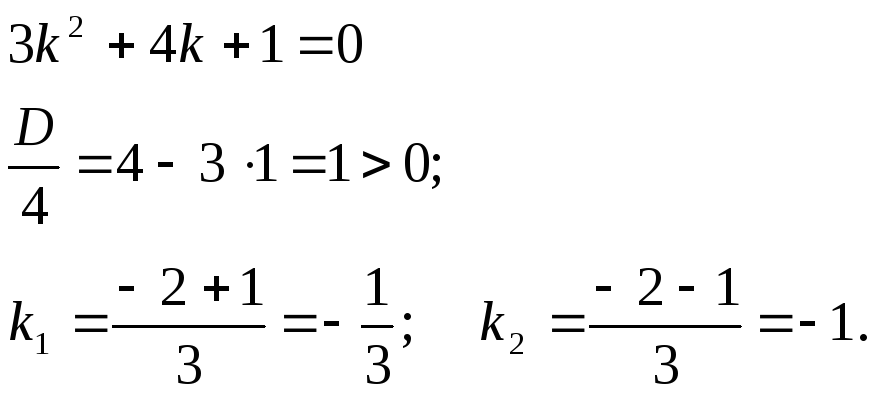
Отже

Тоді

Значить формула справедлива і при n=k+1.

За принципом математичної індукції вона вірна і для будь-якого натурального n.

Приклад №8

Довести методом математичної індукції, що для nєN

Доведення

Запишемо декілька перших значень суми S₁, S₂, S₃, …

Розглядаючи ці функції ми бачимо, що у чисельнику стоять числа, які виражають кількість доданків, а у знаменнику числа виду 3(4n+3).

Тому випливає гіпотеза, що

Доведемо її методом повної математичної індукції.

1) Базис індукції

При n=1 з одного боку

і, з другого боку за гіпотезою

Отже при n=1 рівність має місце.

2) Індуктивний перехід або індуктивний крок.

Припустимо, що дана рівність має місце і при n=k, тобто

Доведемо, що дана рівність має місце і при n=k+1.

За гіпотезою

За означенням суми і формули (k+1) члена маємо

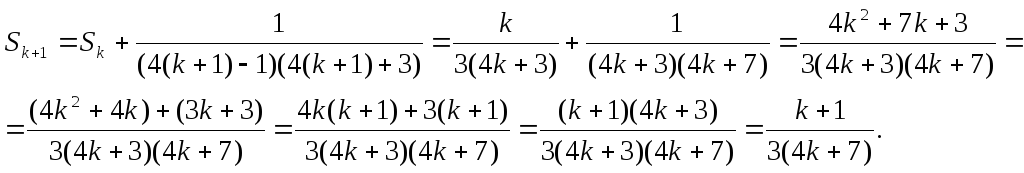
Отже, формула справджується і при n=k+1.

За принципом повної математичної індукції можна зробити висновок, що формула вірна і для будь-якого натурального n.