Приклад №1

Знайти формулу для обчислення суми перших n натуральних чисел S(n)=1+2+3+4+5+…+n;

Розглянемо часні випадки:

n=1 1=1,

n=2 1+2=3,

n=3 1+2+3=6,

n=4 1+2+3+4=10,

n=5 1+2+3+4+5=15.

Очевидно можна зробити припущення, що сума перших n членів натурального ряду S(n)=1+2+3+4+5+…+n=.

Доведемо цю гіпотезу одержану в результаті неповної індукції методом математичної індукції.

Доведення

1. При n=1 1=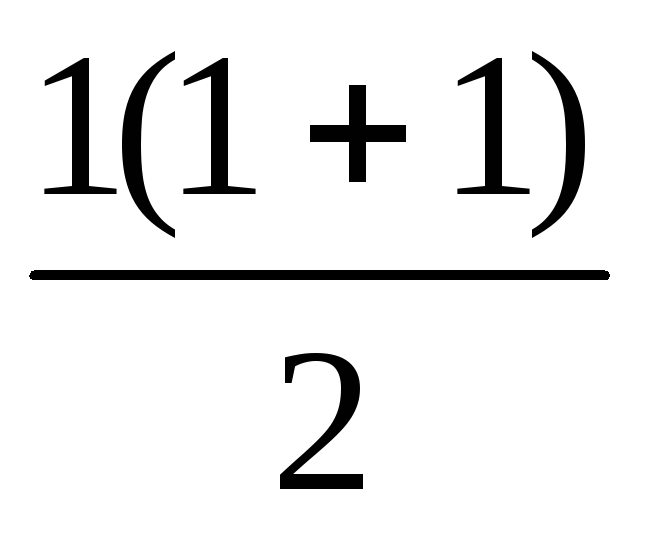=1. Рівність має місце.

2. Припустимо, що вона має місце і при n=k тобто S(k)=1+2+3+4+5+…+k=.

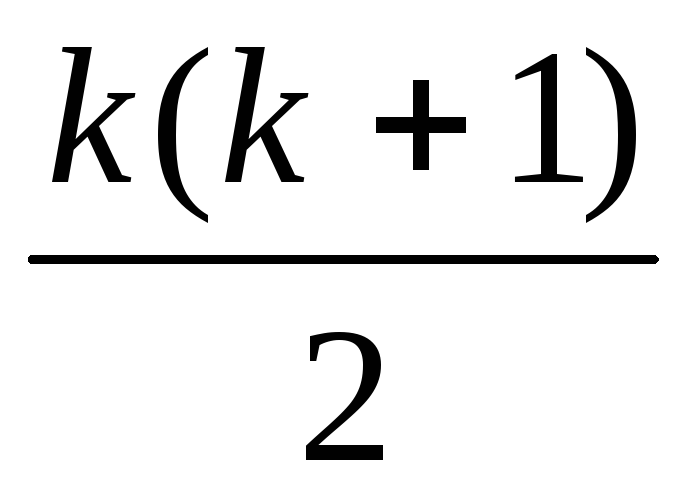Виходячи із цього припущення, доведемо, що воно істине і для n=k+1 тобто, що S(k+1)=. Запишемо S(k+1)=S(k)+(k+1).

Враховуючи припущення, маємо S(k+1)=+k+1==.

Робимо висновок, що формула вірна і при n= k+1.

Тоді за припущенням математичної індукції вона вірна і для будь-якого натурального n. S(n)=1+2+3+4+5+…+n.

Приклад №2

Нехай необхідно знайти суму перших n непарних чисел, тобто

S(n)=1+2+3+4+5+…+(2n-1).

Розглянемо часні випадки:

n=1 1=1=1²,

n=2 1+3=4=2²,

n=3 1+3+5=9=3²,

n=4 1+3+5+7=16=4²,

n=5 1+3+5+7+9=25=5².

Очевидно, що можна зробити припущення, що S(n)=n².

Неповну індукцію ми застосували для того, щоб зробити гіпотезу.

Доведемо її методом математичної індукції.

Доведення

1) Базис індукції:

При n=1 ліва частина складається із одного члену, що дорівнює 1, а права частина дорівнює 1²=1. Отже 1=1. При n=1дана рівність має місце.

2. Індуктивний перехід:

Припустимо, що дана рівність має місце при n=k, тобто 1+3+5+7+9+…+(2k-1)=k².

Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто 1+3+5+7+9+…+(2k-1)+(2k+1)=(k+1)².

Розглянемо ліву частину останньої рівності. За припущенням сума перших k непарних доданків дорівнює k², а тому

1+3+5+7+9+…+(2k-1)+(2k+1)=k²+(2k+1).

k² Отже ця рівність правильна, що і потрібно було довести.

У силу принципу математичної індукції дана рівність має місце і для довільного натурального n.

Приклад №3

Знайти формулу суми S_n=1+2+2²+2³+2⁴+…+2ⁿ⁺¹.

Виконуємо неповну індукцію. Розглянемо окремі випадки:

n=1 1=1= 2¹-1,

n=2 1+2= 3=2²-1,

n=3 1+2+4= 7=2³-1,

n=4 1+2+4+8=15=2³-1,

n=5 1+2+4+8+16=31=2⁴-1.

Можна припустити, що S_n=1+2+2³+2⁵+…+2^n-1=2ⁿ-1.

Доведемо цю гіпотезу методом математичної індукції.

Доведення

1) Базис індукції:

При n=1; S₁=1. S₁=2₁-1=1; 1=1. Формула має місце.

2) Індуктивний перехід:

Припустимо, що дана рівність має місце при n=k, тобто S_k=1+2+2³+2⁵+…+2^k-1=2^k-1.

Доведемо, що S_k+1=2^k-1-1;

S_k+1=S_k+2^k; враховуючи припущення маємо S_k+1=2k^-1-1+2^k=22^k-1=2^k+1-1.

Що і потрібно було довести. Отже, за принципом математичної індукції формула справедлива для будь-якого натурального n.

Аксіоми натуральних чисел. Еквівалентність аксіоми індукції принципу математичної індукції.

Історична довідка. Метод математичної індукції.