Приклад №9

Довести, що при справджується рівність

Доведення

1) При n=1 вірно.

2) Нехай при n=k

Доведемо, що формула вірна і при n=k+1.

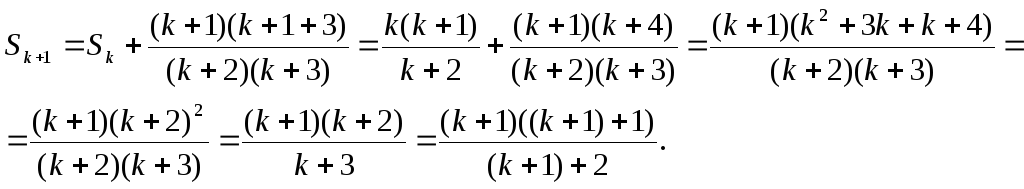
Формула вірна і при n=k+1.

За принципом математичної індукції вона вірна і при будь-якому натуральному

Застосування методу математичної індукції при розв’язуванні геометричних задач

Розглянемо декілька прикладів доведення геометричних тверджень, теорем, у яких найбільш зручним є використання методу математичної індукції.

Приклад №1

Довести, що n різних прямих, які проходять через точку, ділять площину на 2n частин.

Доведення

1)при n=1

Пряма ділить площину на дві півплощини за аксіомою планіметрії.

Отже твердження справджується.

2)Припустимо, що k прямих які проходять через одну точку ділять площину на 2k частин.

Доведемо, що (k+1) прямих 2(k+1)=2k+2 частин.

Дійсно (k+1) пряма, яка проходить через спільну точку всіх прямих додасть ще дві додаткові частини та взагалі кількість частин буде 2k+2=2(k+1).

Отже твердження справедливе.

За припущенням математичної індукції воно буде вірним і при будь-якому .

Приклад №2

У площині проведено n прямих загального положення, тобто жодні дві з них не паралельні і жодні три не перетинаються в одній точці (крім точок A, B, C, але нема прямих, що проходять через дві з цих трьох точок). На скільки частин ділять площину ці прямі?

Розв’язання

Спочатку використаємо неповну індукцію для того, щоб виказати формулу для обчислення кількості прямих, про які йде мова в задачі, а потім доведемо формулу методом математичної індукції.

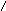
1)при n=1 a

Одна пряма ділить площину на дві

частини за аксіомою планіметрії.

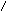
Позначимо N(n) кількість частин,

на які n прямих ділять площину. 1

Тоді можна записати, що 4 2

N(1)=2; 3

3

N(2)= N(1)+2=4;

4 7 2

N(3)= N(2)+3=7; 5 6 1

2 3 7

N(4)= N(3)+4=11.

1 4 6

8

11. 5

9

10

зробимо індуктивне припущення, що N(n)=N(n-1)+n.

Додамо почленно n рівностей:

N(1)+N(2)+N(3)+…+N(n-1)+N(n)=2+N(1)+2+N(2)+2+N(3)+…+N(n-1)+nN(n)=2+2+3+4+5+…+n=1+1+2+3+…+n=.

P.S. S=1+2+3+…+n=Ця формула доведена раніше методом математичної індукції (див. Приклад № У розділі “Доведення рівностей”).

Доведемо, що N(n)=методом математичної індукції

1. Одна пряма ділить площину на дві частини. З іншого боку ,

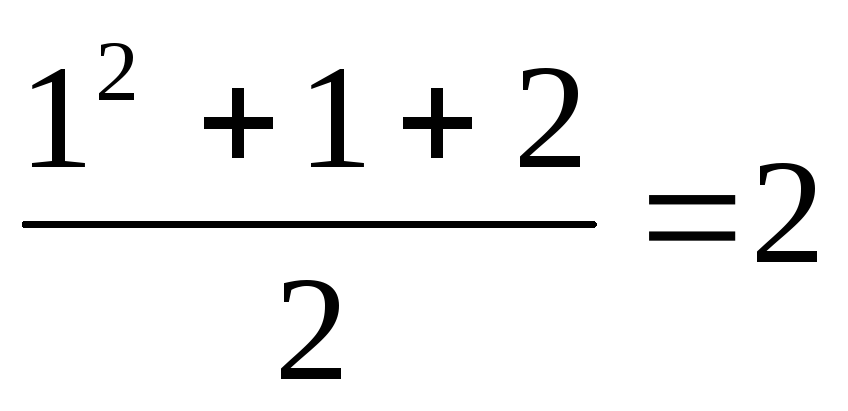тому твердження істине.

2. Припустимо, що k прямих ділять площину на 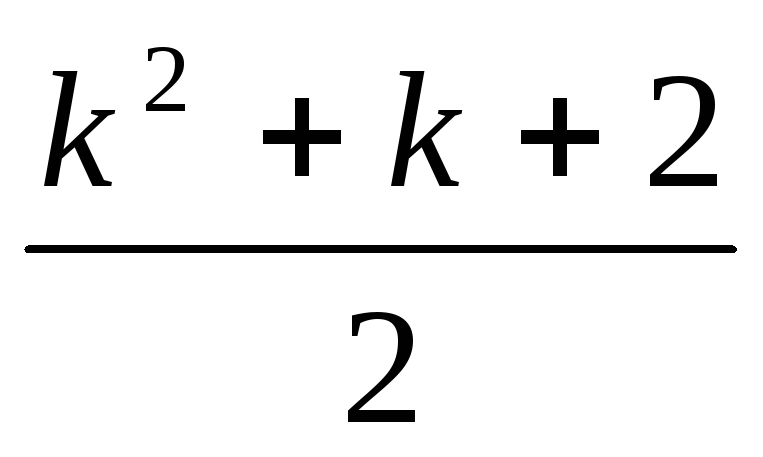частини.

Проведемо (k+1)^шу пряму. Вона не паралельна ні однієї з прямих, тому ця пряма перетне кожну з попередніх прямих, причому точки перетину будуть всі різні (k+1)^ша пряма розтинається виділеними k прямими на (k+1) частину: два променя і (k-1) відрізків.

(k+1)^ша пряма пройде по (k+1) частинам площини і кожну з цих частин поділить ще на 2 частини, тобто кількість частин збільшиться на (k+1) і буде дорівнювати

.

Це означає, що твердження N(n)=має місце і при n=k+1.

За припущенням математичної індукції воно буде справджуватися і при будь-якому натуральному n.