Приклад №6

Довести, що будь-яку суму грошей, більшу 7 копійок, можна розміняти монетами тільки по 3 і 5 копійок.

Доведення.

Нехай сума дорівнює n копійок (n>7); nєN.

1) Якщо n=8, тоді наше твердження A(n) вірне: 8=3+5.

2) Припустимо, що твердження, яке ми позначили A(n), вірне і при n=k,

де k>8, kєN.

Існують два випадки розміну суми у k копійок монетами по 3 і 5 коп.:

а) тільки монетами по 3 коп кожна;

б) виникає потреба хоча б однієї 5 коп монети.

У випадку а) забираємо три монети по 3 коп, додаємо дві по 5 коп і тим самим розмінюємо суму у (k+1) коп, тому що ми додамо до k суми одну копійку.

У випадку б) забираємо одну монету 5 коп; додаємо дві монети по 3 коп кожна і тим самим розмінюємо суму у (k+1) копійку.

Задача розв’язана.

Деякі відомі визначні нерівності і метод математичної індукції

Приклад №1.

Довести, що для будь-якого натурального n .

Доведення.

1) При n=1 ;

n=2 .

Дійсно, a₁ і a₂ мають однакові знаки, або протилежні

Якщо однакові, то ,

Якщо різні, то .

2) Припустимо, що нерівність вірна і для n=k доданків, тобто, що

.

Враховуючи це припущення, доведемо, що нерівність вірна і при n=k+1, тобто покажемо, що .

Дійсно,

.

Отже, нерівність вірна і при n=k+1.

За принципом математичної індукції нерівність справджується для будь-якого натурального n.

Приклад №2.

Нехай х_1, х_2, х_3,…, х_n – довільні додатні числа, причому х₁х₂х₂…х_n=1. Довести, що х₁+х₂+х₂…х_nn.

Доведення.

1. Якщо n=1, тоді х₁=1 за умовою і можна записати х₁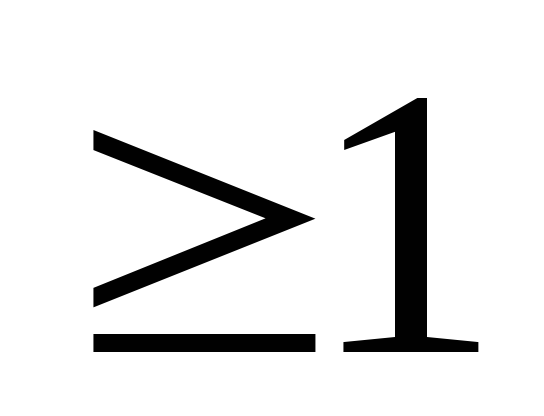, тобто твердження вірне.

2. Зробимо індуктивне припущення. Припустимо, що при n=k твердження вірне, тобто, що х₁+х₂+х₂…х_k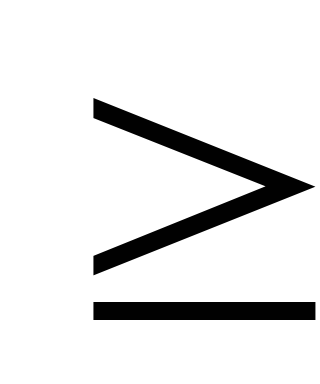k. Числа х_1, х_2, х_3,…, х_k – довільні додатні числа.

Доведемо, що твердження вірне і при n=k+1, тобто що х₁+х₂+х₂…х_k+х_k+1k+1 якщо х₁х₂х₂…х_kx_k+1=1.

Можливі два випадки:

а) кожне з цих чисел дорівнює 1 і тоді їх сума дорівнює k+1 і нерівність доведено.

б) серед цих чисел є хоча б одне число, яке не дорівнює 1 і тоді обов’язково є, по меншій мірі, ще одне число, яке не дорівнює одиниці, причому, якщо одне з них менше одиниці, тоді друге більше 1. Не обмежуючи загальності, можна вважати, що х_k>1, a x_k+1<1. Розглянемо зараз k чисел х_1, х_2, х_3,…, х_k-1, (х_k, х_k+1). Добуток їх дорівнює 1, і значить, за індуктивним припущенням.

х₁+х₂+х₂…х_kх_k+1k. Додамо до обох частин останньої нерівності х_k+х_k+1, а число х_kх_k+1 перенесемо у праву частину.

х₁+х₂+х₂…х_k+х_k+1k+1-1+x_k-x_kx_k+1+x_k+1=k+1+x_k(1-x_k+1)-(1-x_k+1)=

=k+1+(1-x_k+1)(x_k-1)k+1.

Отже А(k+1) справджується тоді за принципом математичної індукції.

х₁+х₂+х₂…х_nn, якщо х₁х₂х₂…х_n=1 при .

Знак рівності має місце тоді і тільки тоді, коли х₁=х₂=х₃=х_n.

Приклад №3

Довідка:

1) Вираз називається середнім арифметичнимn невід’ємних чисел.

2) Вираз називається середнім геометричним невід’ємних чисел.

Має місце нерівність

тобто

Його називають нерівністю Коші на честь французького математика Коші Огюстена Луї (1789-1857 рр), яким написано більш ніж 800 наукових праць.

Існують багато способів доведення цієї нерівності. В більшості з них при доведенні застосовують метод математичної індукції. Наведемо доведення даної нерівності у якому будемо ґрунтуватися на прикладі №2, розглянутому вище.