7.4. Совокупная система

Декомпозиция системы на блоки и возможность их связывания в новые блоки чрезвычайно удобна для пользователя, но при этом мы должны четко осознавать, что совокупную систему уравнений придется строить автоматически. В случае ориентированных блоков построить совокупную систему достаточно просто.

Рассмотрим, какую работу выполняет пользователь, а какую – система моделирования сначала на примере устройства, состоящего из «естественных», наблюдаемых в реальной жизни компонентов.

Пусть нам дана электрическая цепь, изображенная на рис. 28 управляемым извне ключом, значения тока в которой можно в дальнейшем измерять каким-либо прибором. Нам надо построить блок, способный менять свое поведение под действием внешнего, управляющего сигнала («вход») и показать изменения значения тока как функции от времени («выход»). Обсудим возможные подходы.

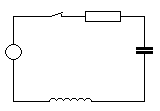
Рис. 28. Электрический контур

Рассмотрим сначала подход, основанный на использовании гибридного автомата.

Наличие ключа в этой цепи говорит о существовании двух режимов работы, то есть мы имеем дело с гибридной системой. Эта гибридная система имеет два состояния, две системы локальных уравнений, и ее невозможно составить из более простых элементов, чем один гибридный автомат, то есть мы не можем сохранить «естественную» структуру цепи, и вынуждены будем вручную строить совокупную систему для всей цепи.

Пусть для начала, мы рассматриваем поведение цепи, в которой в момент происходит замыкание ключа В исходном состоянии автомата ток равен нулю (состояние A1) (рис. 29)

,

а в последующие моменты (состояние A2) определяется уравнением

,

где I, R, C, E – параметры элементов цепи.

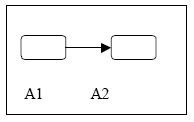
Рис. 29. Гибридный автомат, соответствующий цепи с переключателем

Представленное уравнение составлено на основании закона Кирхгофа и, вместе с заданными начальными условиями I = 0, полностью определяет поведение токов и напряжений в цепи после замыкания ключа.

Предположим, что система моделирования требует представления локального поведения в гибридном автомате в форме систем уравнений первого порядка, разрешенных относительно первых производных. В этом случае мы должны вручную последовательно преобразовать исходное уравнение к виду

,

,

и разрешить полученную систему относительно первых производных:

,

Последняя система и представляет описание поведения «сложной" динамической системы «электрическая цепь», в которой только коэффициенты I, R, C, L, E напоминают о ее компонентной структуре.

Теперь мы можем модифицировать гибридный автомат так, чтобы переключения происходили по сигналу управления. Для простоты используем булевскую переменную Switch, значение true которой трактуется (переход из состояния A1 в A2) как замыкание цепи, а false - как размыкание (переход из состояния A2 в A1) (рис. 30).

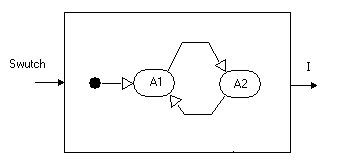
Рис. 30. Карта поведения гибридного автомата электрической цепи

Добавим в описание новые интерфейсные переменные – Switch и I. Совершенно очевидно, что полученная система уравнений написана «правильно», то есть имеет единственное решение и может быть решена численно, но это должен проверить сам пользователь.

Таким образом, в данном случае, когда мы хотим непосредственно воспользоваться формализмом гибридного автомата, мы можем построить только один единственный ориентированный блок, проделав всю необходимую подготовительную работу вручную.

Теперь рассмотрим подход, основанный на передаточных функциях (подход Simulink). Язык пакета Simulink определяет набор ориентированных блоков, из которых следует строить любые системы. Для этого необходимо описать поведение в терминах «вход-выход», а точнее предварительно построить передаточную функцию нужного звена. В данном примере, это особенно просто, так как мы имеем дело с линейным дифференциальным уравнением второго порядка.

Действительно, продифференцируем исходное уравнение цепи (закон Кирхгофа для напряжений), справедливое после замыкания ключа, и получим новое уравнение:

,

которое можно описать на языке передаточных функций.

Используем символику компонентов, принятую в Model Vision Studium и практически не отличающуюся от принятой в пакете Simulink. Разница лишь в том, что в пакете Simulink вы не можете заглянуть «во внутрь» блока и поменять там что-либо по своему желанию, а в MVS такая возможность предусмотрена. Главное, что в обоих пакетах – это ориентированные блоки. На рис. 31 приведены всего четыре элемента, из них два соответствуют блокам с передаточными функциями 1/s и K, обычно называемым интегратором и усилителем соответственно, а последние два – это сумматор и переключатель, они являются вспомогательными и необходимы для получения совокупной системы.

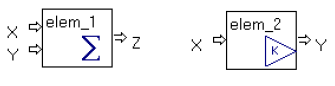
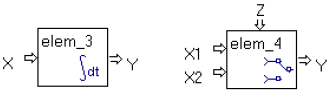
Рис. 31. Блоки, используемые для моделирования электрической цепи

Используя перечисленные блоки, можно построить нужную нам систему (рис. 32).

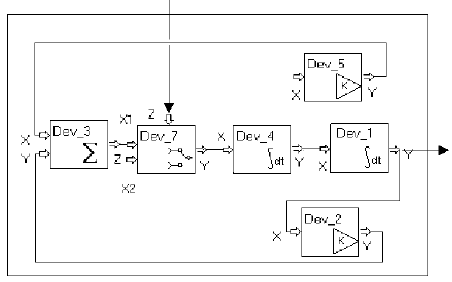
Рис. 32. Функциональная схема электрической цепи, реализованная с помощью «подхода Simulink»

При соединении блоков, в которых для описания внутреннего поведения используются гибридные автоматы с жестко фиксированной формой алгебро-дифференциальных уравнений и разделением фазовых переменных на «входы», «выходы», «состояния», результат объединения всегда приводит к разрешимой системе. Это происходит потому, что эквивалентная локальная система уравнений объединяемых блоков в этом случае является механическим объединением локальных систем уравнений блоков-компонентов. Действительно, в силу свойств «входов» и «выходов», «входы» могут присутствовать только в правых частях дифференциальных уравнении или формул и не могут быть искомым переменным в алгебраических уравнениях. Равенства «вход-выход» и «выход-вход», являющиеся в общем случае алгебраическими уравнениями, соответствующими связям, очевидным образом превращаются в формулы.

Действительно, если «выход» A является источником в ориентированной связи, а «вход» B приемником, то общее алгебраическое уравнение связи 0 = A - B очевидно трансформируется в формулу B = A . Поскольку при численном решении все формулы заменяются на отсортированную последовательность соответствующих операторов присваивания, ясно, что эффективность численного решения для ориентированных связей существенно выше, чем для неориентированных, когда необходимо как минимум решать систему дополнительных алгебраических уравнений, соответствующих связям.

Это свойство ориентированных блоков особенно ценно для моделей гибридных систем, в которых в результате срабатывания переходов в картах состояния локальные системы уравнений могут динамически изменяться и, следовательно, эквивалентная система уравнений тоже должны перестраиваться динамически. В случае ориентированных блоков старые уравнения просто изымаются из эквивалентной системы уравнений, а новые добавляются. При этом формулы, конечно, нужно пересортировывать динамически.

Можно показать, что и в случае использования ориентированных блоков пакета MVS и блоков пакета Simulink мы всегда приходим к совокупной системе алгебро-дифференциальных уравнений, которая и является таким образом «минимальной» по сложности формой описания.