7.5. Неориентированные блоки и связи

Идея использовать в качестве компонентов неориентированные блоки возникла очень давно, и особенно ярко проявляет себя при конструировании электрических схем. Вернемся к описанию электрической цепи (рис. 28), и для простоты рассмотрим только состояние, когда ключ замкнут. Введем две фазовые переменные U и I , а также три элемента R,C,L со следующими компонентными уравнениями:

,

И предположим, что их графические изображения соответствуют рис. 33. На рисунке помимо самого элемента, изображены места соединений – контакты.

Рис. 33. Изображение элемента с контактами

Для реализации цепи необходим еще и источник питания, у которого напряжение постоянно и не зависит от протекающего по цепи тока. Давая имя R1 конкретному элементу, например, сопротивлению, будем предполагать, что этому имени автоматически сопоставляется компонентное уравнение

.

Для описания поведения совокупной системы одних компонентных уравнений недостаточно. Для этого необходимы уравнения, составленные на основании законов Кирхгофа, их также называют топологическими уравнениями, подчеркивая этим зависимость их окончательной формы от конфигурации цепи. Первый закон Кирхгофа утверждает, что сумма токов в любом узле равна нулю, а второй, что сумма падений напряжений в любом замкнутом контуре равна нулю.

При таком подходе пользователю предоставляют возможность рисовать схемы, а программе приходится выявлять на схеме замкнутые контуры и узлы и на их основе получать топологические уравнения.

Покажем, что информации, имеющейся на чертеже электрической схемы достаточно для построения совокупной системы уравнений, определяющей поведение цепи. Электрической схеме с замкнутым ключом поставим в соответствии граф, узлам которого соответствуют контакты. Помеченные дуги соответствуют включенным между контактами элементам (рис. 34).

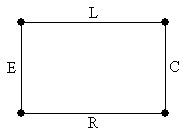
Рис. 34. Граф, узлы которого соответствуют контактам, а дуги – электрическим компонентам

Для этого графа построим нормальное дерево (рис. 35), то есть дерево (связный граф без циклов), охватывающее все узлы, ребра которого образованы включением элементов схемы в определенной последовательности – сначала все источники напряжения, затем элементы C, R, L. Если в состав схема входят источники тока, они включаются в последнюю очередь. (Источники тока сохраняют постоянное значение тока, при любом напряжении.)

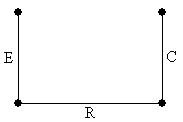
Рис. 35. Нормальное дерево, соответствующее исходному графу

На основании построенного дерева разделим фазовые переменные на две группы. В первую включим токи и напряжения элементов, входящих в состав дерева. В нашем случае это векторы I₁ = [I_E, I_C , I_R] , U₁ = [U_E,U_C,U_R] . Во вторую – остальные, не включенные нами в дерево. У нас в состав дерева не включена дуга, соответствующая индуктивности – I₂ = [I_L] и U₂ = [U_L].

Составим матрицу, столбцами которой являются ребра дерева, а строками – оставшиеся ребра графа.

	E	С	R
L	1	1	1

Выберем направления токов на ребрах и поставим на пересечении соответствующих строк и столбцов следующие знаки:

• плюс единицу, если дуга, указанная в строке, и дуга, указанная в столбце, входят в состав одного цикла, и направления токов у них совпадает;

• минус единицу, если дуга, указанная в строке, и дуга, указанная в столбце, входят в одного состав цикла, но направления токов у них не совпадают,

• ноль, если они не входят в цикл, возникающий при добавлении очередной дуги в дерево (рассмотрение каждой строки этой матрицы эквивалентно добавлению нового ребра в дерево и анализу появившегося цикла).

В нашем, простейшем, случае все элементы матрицы равны единице.

Если обозначить полученную матрицу через M , а транспонированную через M^* , то можно показать, что уравнения:

соответствуют двум рассмотренным топологическим уравнения и имеют вид:

В совокупности с компонентными уравнениями, определенными выше, и с учетом свойства идеального источника напряжения при любом токе в цепи поддерживать на своих контактах постоянное напряжение, получим замкнутую систему уравнений относительно выбранных переменных.

Таким образом, можно получать совокупные системы уравнений для электрических, механических и гидравлических систем, то есть там, где существуют аналоги рассмотренных базовых компонентов и топологические уравнения, аналогичные уравнениям Кирхгофа. Если ввести специальные компоненты, преобразующие один вид энергии в другой, то появляется возможность строить и «смешанные системы», например электромеханические. Алгоритм получения системы уравнений, пригодной для численного интегрирования, достаточно прост благодаря тому, что мы ввели специальные формы компонентных уравнений и сумели правильно учесть уравнения связи, возникающие после соединения элементов через контакты.

Развитием такого подхода, является соединение через контакты блоков, содержащих описание поведения в виде систем алгебраических и дифференциальных уравнений. Основная идея подхода очень удачно выражена в определении «язык для моделирования физических систем». При использовании традиционного подхода блочного моделирования для описания ряда реальных систем возникают серьезные ограничения на вид блоков.

Библиографический список

1. Зарубин В.С. Математическое моделирование в технике. М: Изд-во МГТУ им. Н.Э.Баумана, 2001.

2. Лоу А.М., Кельтон Д.В. Имитационное моделирование (Simulation Modeling and Analysis. Серия: Классика Computer Science). СПб.: Питер, 2004.

3. Бенькович Е. Практическое моделирование динамических систем / Е. Бенькович, Ю. Колесов, Ю. Сеничков. СПб.: БХВ-Петербург, 2002.

4. Карпов Ю. Имитационное моделирование систем. Введение в моделирование с AnyLodic 5. – СПб.: БХВ-Петербург, 2005.

5. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М.: ФИЗМАТЛИТ, 2002.

6. Дьяконов В.П., Круглов В.И. MATLAB. Анализ, идентификация и моделирование. СПб.: Питер, 2002.

7. Бахвалов Л. Компьютерное моделирование – длинный путь к сияющим вершинам / Компьютерра, 6.10.1997г., № 40(217), С.26-36.

8. Шеннон Р. Имитационное моделирование систем - искусство и наука. М.: Мир, 1978.-418с.