Лекция по сопромату

Jz0

J y0

Jz0 y0

n
= ∑(Jz 0i	+bi2 Ai) .	(3.5)
i=1
n
= ∑(J y0i	+ai2 Ai ) .	(3.6)
i=1
n
= ∑(Jz0i y0i +aibi Ai) .		(3.7)
i=1

Расчёт можно предельно формализовать, подставив выражения (3.4) в формулы (3.5), (3.6), (3.7). В этом случае предварительный расчёт сводится к выполнению пункта 4. Пункты 2 и 3 необязательны для вычисления моментов инерции сложной фигуры.

	n
Jz0	= ∑(Jz0i	+( yci − yc )2	Ai ) .	(3.8)
	i=1
	n
J y0	= ∑(J y0i	+(zci − zc )2	Ai ) .	(3.9)
n	i=1
Jz0 y0 = ∑(Jz0i y0i +(zci − zc )( yci − yc )Ai ) .				(3.10)
i=1

Вопросы для самопроверки

1.Как вычисляются моменты инерции прямоугольника относительно центральных осей, параллельных сторонам прямоугольника?

2.Можно ли при определении моментов инерции сложных фигур вычислять не сумму, а разность моментов инерции простых фигур?

31

ЛЕКЦИЯ 4. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

Практические вычисления представлены в примере 2. Пример 2. Рассчитана фигура, рассмотренная в примере 1.

Во избежание ошибок по невнимательности полезно выполнить чертёж сечения (рис. 4.1) с указанием центральных осей всего сечения и центральных осей каждой простой фигуры, т. е. выполнить пункт 2 последовательности вычисления моментов инерции сложной фигуры (см. лекцию 3).

	y	y0 y02
	y01
	y03	2

•

	•
1	•

yc

•

zc 3

z02

z01

z0

z

z03

Рис. 4.1. Чертёж фигуры с центральными осями

Далее выполняется пункт 4. Выписываются формулы для моментов инерции простых фигур относительно центральных осей (рис. 4.2–4.4).

32

y

h

•

b

z

h •

b

	y
c	•
y

D

Jz

=

bh3

;

J y

=

hb3

.

z

36

36

b2h2

Jzy = ±

72 .

Рис. 4.2. Треугольник

y

Jz

=

bh3

;

J y

=

hb3

.

12

12

J zy

= 0 .

Рис. 4.3. Прямоугольник

y =	2D	.
c	3π
z Jz =0,11R4 ;	J y =		πD4 .
			128
R = D/2;	Jzy = 0.

Рис. 4.4. Полукруг

Для каждой фигуры по приведённым формулам вычисляются моменты инерции в соответствии с заданными размерами. При выборе табличной формулы необходимо сопоставлять расположение фигуры в таблице и в заданном сечении. Результаты вычислений заносятся в таблицу.

33

Моменты инерции простых фигур

Фигура № 1				Фигура № 2				Фигура № 3
Jz01	, см4	47,64	Jz02		, см4	114,33	Jz03		, см4	45,1
Jy01	, см4	24,3	Jy02		, см4	37,33	Jy03		, см4	161,03
Jz y	, см4	17	Jz y		, см4	0	Jz y		, см4	0
01	01		02	02			03	03

Значения моментов инерции в таблице и результаты примера 1 ( yci ; yc ; zci ; zc ) подставляются в формулы (3.8) – (3.10)

и вычисляются моменты инерции всего сечения:

Jz0 = 682,55 см4; J y0 =389,26 см4; Jz0 y0 =164,44 см4.

4.1. Зависимость между моментами инерции при повороте осей

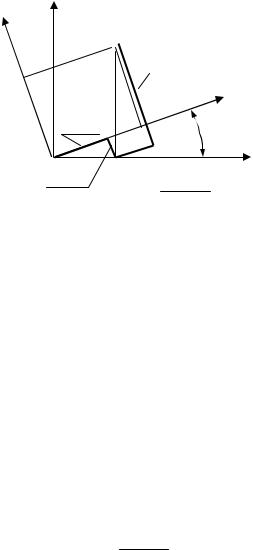
Через центр тяжести поперечного сечения можно провести бесчисленное множество координатных осей. Для расчётов на прочность важно знать, какое положение занимают центральные оси, относительно которых моменты инерции имеют экстремальные значения, т. е. один момент инерции является максимальным, а второй – минимальным. Положение этих особых осей координат выявляется при рассмотрении зависимости между моментами инерции относительно осей исходных и повёрнутых на угол α (рис. 4.5).

Зависимость между моментами инерции при повороте осей может быть установлена на основе выражений (2.10) – (2.12) путём непосредственных преобразований. Исходными для тожде-

ственных преобразований являются формулы
u = z cos α+ y sin α; v = y cos α−z sin α.	(4.1)

Формулы (4.1) получаются на основе комбинации длин отрезков, показанных на рис. 4.5.

34

y

v

	z	•
	u		y cosα
	y	v		u

z cosα	α
	z

z sin α y sin α

Рис. 4.5. Координаты произвольной точки в исходной и повёрнутой системах координат

Из формул (2.10) – (2.12) сиспользованием(4.1) получается:

Ju = Jz cos2 α+ J y sin2 α− Jzy sin(2α) ;	(4.2)
Jv = Jz sin2 α+ J y cos2 α+ Jzy sin(2α) ;	(4.3)
Juv = Jzy cos 2α+ 1 (Jz − Jy )sin(2α) .	(4.4)
2

Вопрос о том, при каком угле α моменты инерции Ju, Jv принимают экстремальные значения, решается по известной процедуре математического анализа: берётся производная, приравнивается нулю, из полученного уравнения определяется аргумент экстремального значения функции. Исследование функций Ju, Jv на экстремум даёт один и тот же результат для определения α:

tg(2α) =	2Jzy
	J y − J z .	(4.5)

Эта же формула получается из условия Juv = 0. Таким образом, по формуле (4.5) определяется особое положение централь-

35

ных осей, которые называются главными осями. Их отличие от других центральных осей подчёркивается в определении: глав-

ными центральными осями называются центральные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения (один максимальный, другой минимальный).

Моменты инерции относительно главных центральных осей называются главными моментами инерции.

По формуле (4.5) вычисляется tg(2α) , затем угол 2α

и, наконец, угол поворота α, определяющий положение главных центральных осей.

Главные моменты инерции можно вычислить не только по формулам (4.2), (4.3). Моменты инерции – это элементы матрицы I.

Jz		J zy
I =		J		.
J	zy		y

В задаче на собственные значения для матрицы I решается уравнение

(J z − J )	J zy		= 0 .
Jzy	(J y − J )

После раскрытия определителя получаются формулы для вычисления главных моментов инерции.

Jmax =

J

z

+ J

y

+

J

z

− J

y

2

+ Jzy2 .

(4.6)

2

2

Jmin =

J

z

+ J

y

−

J

z

− J

y

2

+ Jzy2 .

(4.7)

2

2

По формулам (4.6), (4.7) можно вычислить значения главных моментов, но важно знать не только величину главного мо-

36

мента, но и к какой оси он относится. Обе эти задачи решаются по формулам (4.2), (4.3), а формулы (4.6), (4.7) используются как проверочные. Кроме того, линейные преобразования матрицы не изменяют величину её определителя, поэтому справедливо уравнение

	Jz	Jzy		=		Jmax	0		.
	Jzy	J y				0	Jmin
После раскрытия определителей получается:
	Jmax Jmin = Jz J y − J zy2 .									(4.8)
При линейных отображениях след матрицы не изменяется,
поэтому справедливо уравнение
	Jz + J y = Jmax + Jmin .									(4.9)
Выражения (4.8), (4.9) используются для проверки вычис-
лений.
Пример 3. Рассчитана					сложная		фигура,			представленная

в примерах 1, 2. В примере 2 вычислены моменты инерции отно-

сительно центральных осей: Jz			= 682,55 см4; J y =389, 26 см4;
			0	0
Jz	0	y =164,44 см4. После подстановки этих значений в (4.5) по-
		0
лучается tg(2α) = –1,121. Угол			2α	равен 2α = arctg(–1,121) =

= 48,274°. Тогда α = –24,137°. Главные центральные оси повёрнуты относительно осей z0, y0, какпоказано на рис. 4.6.

Тригонометрические функции угла α равны: sin2α = 0,1672; cos2 = 0,8328; sin(2α) = –0,7463. Эти значения функций подстав-

ляются в (4.2), (4.3). Главные моменты инерции равны:

Ju = 756,24 см4; Jv = 315,57 см4. Значения главных моментов, вычисленных по формулам (4.6), (4.7): Jmax = 756,23 см4,

Jmin = 315,57 см4.

Проверка вычислений по выражениям (4.8), (4.9).

37

Jmax Jmin	= Jz	J y	− Jz2 y .
	0	0	0	0
238643,5		238648,9

Jz0 + J y0 = Jmax + Jmin .

1071,81 1071,8

y y0 v

2

1	•	z0
		z
		α
	3	u

Рис. 4.6. Главныецентральныеосипоперечногосечения

Вопросы для самопроверки

1.Какие оси координат называются главными центральными осями?

2.Как проверить вычисление моментов инерции сложных фигур относительно произвольных центральных осей?

38

ЛЕКЦИЯ 5. ВНУТРЕННИЕ УСИЛИЯ И НАПРЯЖЕНИЯ

ПРИ РАСТЯЖЕНИИ-СЖАТИИ

5.1. Растяжение-сжатие

По общему определению при простом виде деформации в поперечном сечении действует только одно внутреннее усилие. Тогда растяжение или сжатие стержня определяется следующим образом: растяжение-сжатие – это такой простой вид деформации, при котором в поперечном сечении действует только продольная сила N.

Во второй лекции получена зависимость (2.1) N = ∫σdA .

A

Теперь для решения задачи о прочности необходимо взять интеграл. Из курса математики известно, что для взятия интеграла должна быть известна подынтегральная функция, т. е. σ( А) , од-

нако в сопротивлении материалов нет дополнительных уравнений, позволяющих определить эту функцию. Если задача не решается математически, то её решают экспериментально. В лабораторных условиях установлено, что точки на поверхности стержня, находящиеся на контуре одного и того же поперечного сечения, перемещаются одинаково. Этот факт устанавливается прямыми замерами перемещений точек с помощью специальных приборов. Перемещения точек внутри стержня замерить невозможно, поэтому остаётся только один вариант – предположить, что точки поперечного сечения внутри тела перемещаются так же, как точки на поверхности, т. е. одинаково. Другими словами, при деформации растяжения-сжатия поперечное сечение остаётся плоским, перемещаясь параллельно самому себе вдоль продольной оси стержня. Таким образом, сформулировано допущение о плоских сечениях – сечение, плоское до деформации, остаётся плоским после деформации. Впервые допущение о плоских сечениях ввёл Даниил Бернулли (1700–1782).

39

Естественно предположить, что напряжения распределяются по площади поперечного сечения так же, как перемещения. Тогда согласно допущению о плоских сечениях σ(A) =const .

Формула (2.1) легко интегрируется.

N = ∫σdA N = σ∫dA N = σA .

A A

Отсюда получается формула для вычисления нормальных напряжений при растяжении-сжатии.

σ=	N	.	(5.1)
	A

Интегральная формула (2.1) заменяется алгебраической формулой (5.1), т. е. сделан шаг по схеме Р. Декарта: математическая задача заменяется алгебраической. Формула (5.1) позволяет вычислить величину нормальных напряжений от заданной нагрузки, т. к. от заданной нагрузки и вида закрепления стержня зависит величина продольной силы. Тогда следующий шаг в решении задачи о прочности – это определение продольных сил, исходя из заданной расчётной схемы конструкции.

5.2. Определение продольных сил

Любые внутренние усилия, в том числе и продольные силы, определяются методом сечений, известным из курса теоретической механики. Последовательность применения метода сечений состоит в следующем.

1)После определения реакций опор конструкция мысленно разделяется на две части.

2)Одна из частей отбрасывается (обычно отбрасывается более сложная, громоздкая часть).

3)Действие отброшенной части на оставшуюся часть заменяется внутренними усилиями.

40