Лекция по сопромату

иудлинений стержня ( l). Результаты измерений оформляются в виде графика, который называется диаграммой. Эксперименты показывают, что различные материалы могут иметь качественно одинаковые диаграммы. По диаграммам растяжения материалы разделяются всего лишь на две группы: пластичные материалы

ихрупкие материалы. Диаграмма растяжения пластичного материала (углеродистой стали) представлена на рис. 6.4.

σ

	•		•	•
σт	•				σв
		σ
			п	σу

ε

Рис. 6.4. Диаграммарастяженияпластичногоматериала

Ось абсцисс обозначена ε – относительная линейная деформация (ε = l/l, где l – начальная длина стержня).

На диаграмме отмечены характерные точки, соответствующие предельным значениям напряжений:

σп – предел пропорциональности – наибольшее напряже-

ние, до которого материал деформируется в соответствии с законом Гука (по закону Гука напряжения линейно зависят от деформаций);

σу – предел упругости – наибольшее напряжение, до которо-

го в материале развиваются только упругие деформации (упругими называются деформации, исчезающие после снятия нагрузки); σт – предел текучести – напряжение, при котором резко увеличиваются пластические деформации без увеличения на-

51

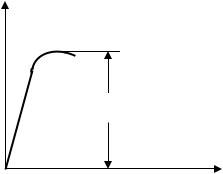
грузки (пластическими называются деформации, остающиеся после снятия нагрузки);

σв – предел прочности или временное сопротивление – ус-

ловно наибольшее напряжение в материале как отношение наибольшей силы к первоначальной площади поперечного сечения.

Диаграмма растяжения хрупкого материала показана на рис. 6.5.

σ

σв

ε

Рис. 6.5. Диаграммарастяженияхрупкогоматериала

Диаграмма на рис. 6.5 показывает, что в хрупких материалах пластические деформации практически отсутствуют.

Диаграммы растяжения пластичных и хрупких материалов имеют линейные участки, графически изображающие закон Гука: σ = Eε . Здесь Е – коэффициент пропорциональности, называемый модулем упругости (ввёл Томас Юнг (1773–1829)). По своему физическому смыслу модуль упругости – это напряжение, которое могло бы возникнуть в материале при упругих относительных деформациях ε =1, т. е. увеличении длины стержня в два раза ( l = l).

Кроме продольной деформации при растяжении-сжатии возникает поперечная деформация (εп), характеризующая изменение размеров поперечного сечения. В пределах упругих деформаций зависимость между поперечной и продольной дефор-

52

мациями является линейной: εп = με, где μ – коэффициент Пуассона (Симеон Дени Пуассон (1781–1840)).

Модуль упругости Е и коэффициент Пуассона μ называются физическими характеристиками материала, и определяются экспериментально для каждого материала.

6.4. Условие прочности при растяжении-сжатии

Результаты экспериментов показывают, что существует два вида деформаций: упругие и пластические. Упругие деформации очень малы и практически не изменяют первоначальные размеры и форму конструкции. Пластические деформации существенно изменяют размеры и форму конструкции ещё до разрушения материала. Для большинства строительных конструкций и механических систем значительное отклонение от первоначальных размеров в процессе эксплуатации не допускается. В связи с этим прочной считается не та конструкция, которая не разрушается, а та, в которой нет пластических деформаций. Контролировать вид деформации можно, устанавливая такую величину максимальных напряжений в материале, при которой развитие пластических деформаций невозможно. Такие напряжения называются допускаемыми. Допускаемые напряжения –

это наибольшие напряжения в конструкции, обеспечивающие упругую работу материала. Обозначение допускаемых напряжений – [σ] . Для пластичных материалов допускаемые

напряжения определяются по формуле

[σ] =	σт ,	(6.5)
	n

где n – коэффициент запаса прочности, величина которого назначается по нормативным документам в зависимости от класса конструкции.

Для хрупких материалов

53

[σ] =	σв .	(6.6)
	n

Таким образом, чтобы обеспечить упругую работу материала необходимо выполнение условия прочности: максималь-

ные напряжения от нагрузки должны быть меньше или равны допускаемым напряжениям.

σmax ≤[σ] .

(6.7)

С учётом формулы (6.1) условие прочности принимает вид

	N	≤[σ].	(6.8)
	A max

Для стержней постоянного сечения с учётом (6.2) условие прочности имеет вид

Nmax	≤[σ] .	(6.9)
A

Физический смысл условия прочности состоит в том, что под прочностью понимается только упругая работа материала. Если в конструкции появились пластические деформации без разрушения материала, то конструкция считается не прочной. В этом заключается точный инженерный смысл понятия прочности, отличающийся от обыденных представлений, описанных в первой лекции. По своему месту в схеме Декарта условие прочности представляет собой третий пункт, т. е. сводит алгебраическую задачу к арифметической. Имея условие прочности, можно производить арифметические действия – расчёты на прочность. Условие прочности используется в трёх вариантах.

1) Проектировочный расчёт. Задаётся расчётная схема и материал. Определить размеры поперечного сечения. Для участка с постоянными величинами N и A площадь сечения определяется из условия прочности по формуле

54

A ≥	N	.	(6.10)
	[σ]

При известной площади и компоновке сечения определяется геометрический параметр поперечного сечения.

2) Определение грузоподъёмности. Нагрузка выражена через параметр, который требуется определить при известных размерах и материале конструкции.

Сначала из условия прочности определяется допускаемая продольная сила.

[N] = A [σ] .

(6.11)

Затем продольная сила, соответствующая максимальным напряжениям, выражается через параметр нагрузки и приравнивается к допускаемой силе. Из полученного уравнения вычисляется параметр допускаемой нагрузки (грузоподъёмность).

3) Проверочный расчёт. Известны все факторы, влияющие на прочность. Проверяется выполнение условия прочности. Если условие прочности не удовлетворяется, производится проектировочный расчёт или определяется грузоподъёмность.

Пример 6. Рассматривается расчётная схема стержня, данного в примере 4.

Проектировочный расчёт. Пусть материал стержня – углеродистая сталь, допускаемые напряжения равны [σ] = 160 МПа.

При постоянном по длине круглом сечении площадь определяется по формуле (6.10)

A ≥ N[σmax] A ≥ 3016010−3 104 = 1,875 см2.

Тогда диаметр стержня равен:

	D =	4A	=	4 1,875	= 1,5451 см.
		π		π

55

Впримере 5 рассмотрен стержень переменного сечения

сотношением площадей А1 = А2 = А, А3 = 4А, А4 = 2А. Эпюра напряжений в примере 5 показывает, что при заданном соот-

ношении площадей максимальные напряжения возникают на первом участке. Условие прочности для первого участка записывается в виде

NA1 ≤[σ] .

Тогда параметр площади равен:

A = [Nσ1] =1016010−3 104 = 0,625 см2.

При известном параметре А площади на участках определяются по заданным соотношениям.

Вопросы для самопроверки

1.Как используется допущение о плоских сечениях при переходе от математической задачи к алгебраической?

2.Для чего изучается напряжённое состояние в точке?

3.На каких площадках действуют максимальные нормальные напряжения в точке при растяжении-сжатии?

4.На каких площадках действуют максимальные касательные напряжения в точке при растяжении-сжатии?

5.Какие предельные напряжения определяются достаточно точно в процессе эксперимента?

6.Как определяются допускаемые напряжения для пластичных и хрупких материалов?

7.Каков физический смысл условия прочности?

8.Почему условие прочности является результатом перехода от алгебраической задачи к арифметической задаче сопротивления материалов?

9.Какова роль эксперимента в сопротивлении материалов?

56

ЛЕКЦИЯ7. СТАТИЧЕСКИНЕОПРЕДЕЛИМЫЕСИСТЕМЫ

ПРИ РАСТЯЖЕНИИ-СЖАТИИ

7.1. Перемещения при растяжении-сжатии

В соответствии с формулами для напряжений ( σ = N / A ) и относительных деформаций (ε = l/l) закон Гука ( σ = Eε) переписывается в виде

NA = E ll .

Отсюда определяется абсолютное удлинение участка стержня длиной l при постоянной площади сечения и постоянной продольной силе.

l =	Nl	.	(7.12)
	EA

Изменение длины участка можно трактовать как относительное перемещение крайних сечений участка (u) (рис. 7.1).

N

N

a

l

a

Перемещение

правого

l = 2a

торцевого

сечения

относительно

левого

l

u = l

торцевого

сечения

Рис. 7.1. Относительноеперемещениекрайнихсечений участка

Для получения полной информации о деформировании конструкции строится эпюра перемещений.

57

Пример 7. Рассчитан стержень, представленный в примере 4. Пусть стержень имеет постоянную по длине площадь, вычисленную в примере 6 (А = 1,875 см2). Модуль упругости стали

равен Е = 2 105 МПа.

Для построения эпюры перемещений желательно выбрать опорное сечение с нулевым перемещением, относительно которого определяются перемещения крайних сечений участков. Эти перемещения показываются на эпюре. Перемещения крайних сечений участков соединяются прямыми линиями, т. к. внутри участка в соответствии с формулой (7.12) зависимость перемещений от длины линейна. Крайние сечения участков обозначены на схеме конструкции 0, a, b, c, d (рис. 7.2).

F1 = 10 кН

F2 = 30 кН F3 = 40 кН

F4 = 10 кН

0

a

b

c

d

0,6 м

0,3 м

0,8 м

0,6 м

1,6

8

6,4

эп. u

(10-4м)

Рис. 7.2. Эпюра продольныхперемещений

Вычисление перемещений.

Опорное сечение 0 не перемещается, поэтому u0 = 0. Перемещение сечения а относительно сечения 0 вычисляется по фор-

муле (7.12): ua−0	=		10 10−3 0,			6		=1,6 10−4 м. Перемещение сече-
			10	5	1,875	10	−4
	2

ния b относительно сечения 0 определяется как сумма перемещения сечения b относительно сечения а ( ub−a ) и перемещения

58

сечения а относительно сечения 0 ( ua−0 ): ub−0 =ub−a +ua−0 . Перемещение ub−a определяется по формуле (6.12). Так как N2 = 0,

перемещение ub−a =

0. Тогда перемещение

ub−0 =1,6 10−4 м.

Аналогично определяются

перемещения сечений

c и d:

uc−0 = uc−b +ub−0 ;

ud−0 = ud −c +uc−0 .

Перемещения

uc−b ; ud −c

определяются по формуле (7.12).

u

=

N l

=

30 10−3 0,8

= 6, 4 10

−

4 м.

c−b

3 3

EA

2 105 1,875 10−4

u

d −c

=

N4l4

=

−10 10−3 0,6

= −1,6 10−4 м.

EA

2 105 1,875 10−4

С учётом вычисленных перемещений получается:

u

=8 10−4 м;

u

d −0

=6,4 10−4 м.

c−0

По вычисленным значениям перемещений строится эпюра перемещений, показанная на рис. 7.2.

7.2. Статически неопределимые системы, работающие на растяжение-сжатие

Для плоской системы сил можно составить три независимых уравнения статики, поэтому число реакций не должно быть меньше трёх. Если силы действуют вдоль одной прямой, то составляется только одно уравнение статики, которое может выполняться за счёт одной реакции опоры. Системы, имеющие

недостаточное число реакций для выполнения всех уравнений статики, называются механизмами. Другими словами,

если конструкция не имеет минимально необходимого числа реакций опор, она падает. Минимально необходимое число реакций опор равно числу уравнений статики. Системы, в которых

число реакций опор равно числу уравнений статики, назы-

59

ваются статически определимыми. Довольно часто по техно-

логическим причинам конструкция имеет реакций больше минимально необходимого числа. Системы, в которых число ре-

акций опор больше числа уравнений статики, называются статически неопределимыми. Для расчёта статически неопределимых систем к уравнениям статики дополнительно составляются так называемые уравнения совместности перемещений. Число уравнений статики и уравнений совместности перемещений должно равняться числу неизвестных усилий. Уравнения совместности перемещений составляются на основе анализа деформации конструкции. В результате анализа устанавливаются количественные соотношения между перемещениями отдельных точек системы. Эти количественные соотношения выражаются в виде уравнения совместности перемещений. Таким образом,

уравнение совместности перемещений выражает геометрические особенности деформации конструкции.

Так как различные конструкции имеют свои отличные друг от друга особенности деформирования, общей схемы составления уравнений совместности перемещений не существует. Безошибочно можно выявить особенности деформирования простых конструкций, и эти особенности записать в виде уравнений. Для расчёта сложных статически неопределимых конструкций существуют специальные методы, которые рассматриваются по курсу строительной механики.

В рамках курса сопротивления материалов рассчитываются простые конструкции, представленные в последующих примерах.

Пример 8. Расчётная схема конструкции представлена на рис. 7.3. Цель расчёта – построение эпюры продольных сил. Конструкция имеет две опоры с реакциями Ra , Rb . Так как все

силы действуют вдоль оси стержня, существует одно уравнение статики ∑Fx = 0 или

Ra + F1 + F2 −F3 + Rb = 0 .

60