
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,
7. Уравнения прямой в пространстве:
общие уравнения прямой в пространстве (уравнения прямой как линии пересечения двух непараллельных плоскостей) A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0:
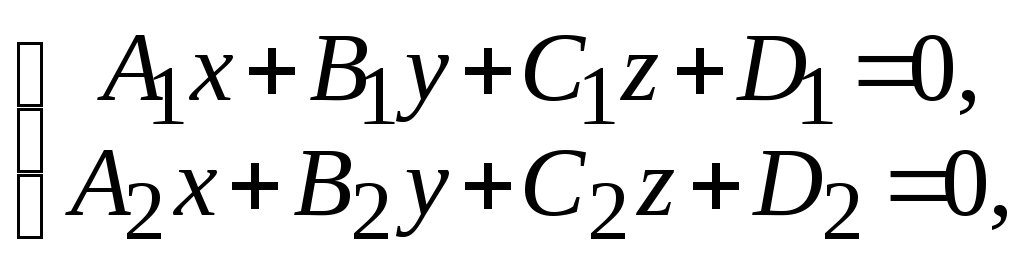
направляющий
вектор этой прямой а
= N1N2
=
 ,
а точка на прямой определяется решением
системы при фиксированном значении
одной из переменных, например, приz0
= 0 значения x0,
y0
являются решением системы
,
а точка на прямой определяется решением
системы при фиксированном значении
одной из переменных, например, приz0
= 0 значения x0,
y0
являются решением системы

канонические уравнения прямой – уравнения прямой, проходящей через точку М(x0; y0; z0), с заданным направляющим вектором a = {ax; ay; az}:
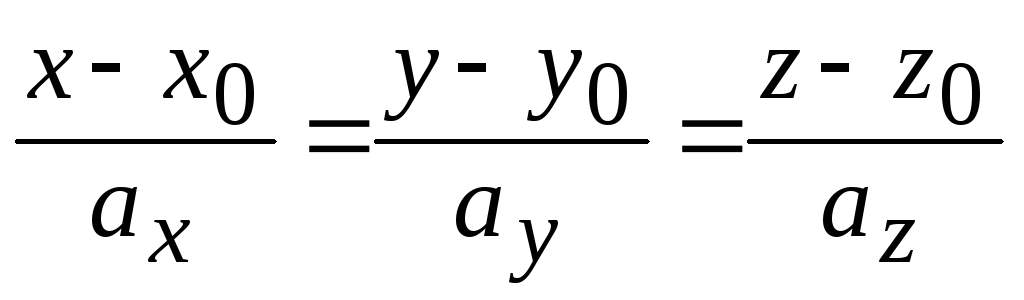 ;
;уравнения прямой, проходящей через две точки М1(x1; y1; z1), М2(x2; y2; z2):
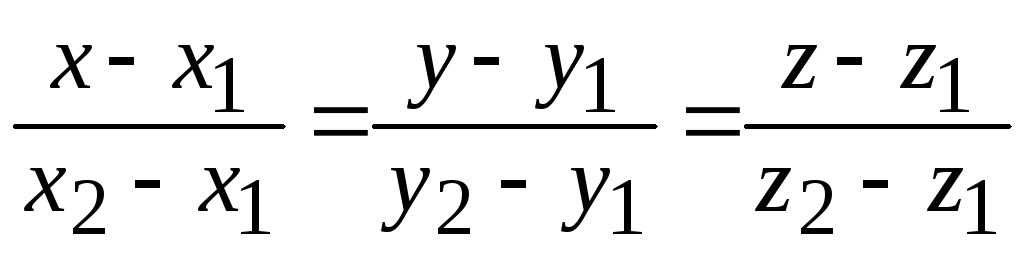 ;
;параметрические уравнения прямой, проходящей через точку М(x0; y0; z0), с заданным направляющим вектором a = {ax; ay; az}: х = х0 +t·ax; y = y0 +t·ay; z = z0 + t·az.
8.
Угол между прямой и плоскостью
– острый угол
между прямой
и ее проекцией на плоскость; если прямая
задана каноническими уравнениями
![]() ,
а плоскость – общим уравнениемAx
+
By
+
Cz
+
D
= 0,
то sin
=
,
а плоскость – общим уравнениемAx
+
By
+
Cz
+
D
= 0,
то sin
=
![]() ,
гдеN
= {A;
B;
С}
– нормальный вектор плоскости, a
= {ax;
ay;
az}
– направляющий вектор прямой.
,
гдеN
= {A;
B;
С}
– нормальный вектор плоскости, a
= {ax;
ay;
az}
– направляющий вектор прямой.
9. Угол между двумя прямыми в пространстве: если известны направляющие векторы a1 и a2 двух прямых в пространстве соответственно, то косинус острого угла a между этими прямыми:
cos
=
![]() .
.
Примеры выполнения заданий лабораторной работы
1. Написать уравнения прямых, проходящих через точку М(– 2; 1), одна из которых параллельна, а другая – перпендикулярна заданной прямой l: 5x + 3y – 4 = 0. Выполнить чертеж.
Решение.
Прямая l: 5x + 3y – 4 = 0, задана общим уравнением на плоскости. Ее нормальный вектор N = {5; 3}, направляющий вектор а = {3; – 5}.
а) Находим уравнение прямой l1, перпендикулярной прямой l. Для l1 нормальным вектором N1 является вектор а, т.е. N1 = {3; – 5}. Записываем уравнение прямой l1 по заданному нормальному вектору N1 = {3; – 5} и точке М(– 2; 1), через которую эта прямая проходит: 3(х + 2) – 5(у – 1) = 0, т.е. l1: 3х – 5у + 11 = 0.
б) Находим уравнение прямой l2, параллельной прямой l. Для l2 нормальным вектором N1 является вектор N, т.е. N2 = {5; 3}. Записываем уравнение прямой l2 по заданному нормальному вектору N2 = {5; 3} и точке М(– 2; 1), через которую эта прямая проходит: 5(х + 2) + 3(у – 1) = 0, т.е. l2: 5х + 3у + 7 = 0.
в) Чтобы построить графики прямых l1, l2, l, определим по 2 точки для каждой из этих прямых, через которые они проходят (одна точка для l1 и l2 уже задана: М(– 2; 1)). Для этого, задавая, например значение х, по уравнению соответствующей прямой найдем координату у искомой точки:
|
l1: |
х |
–2 |
3 |
|
l2: |
х |
–2 |
1 |
|
l: |
х |
2 |
– 1 |
|
у |
1 |
4 |
|
у |
1 |
– 4 |
|
у |
–2 |
3 |
Т.о., прямая l1 проходит через точки М(– 2; 1) и М1(3; 4); прямая l2 проходит через точки М(– 2; 1) и М2(1; – 4); прямая l проходит через точки М3(2; – 2) и М4(– 1; 3):

Ответ: l1: 3х – 5у + 11 = 0 (l1 l); l2: 5х + 3у + 7 = 0 (l2 || l).
2. Написать уравнения прямой, которая проходит через точку М(6; 5) и через точку пересечения прямых l1: x – y + 3 = 0, и l2: 5x – 3y – 1 = 0. Выполнить чертеж.
Решение.
Находим
точку пересечения М1
прямых l1
и l2:
![]() .
Решая эту систему, например, по формулам
Крамера, получаем координаты этой точки:М1(5;
8).
.
Решая эту систему, например, по формулам
Крамера, получаем координаты этой точки:М1(5;
8).
Записываем
искомое уравнение прямой l,
проходящей через точки М(6;
5)
и М1(5;
8)
на плоскости:
![]() =
0, гдех1
=
6; у1
= 5;
х2
= 5;
у2
= 8,
т.е.:
=
0, гдех1
=
6; у1
= 5;
х2
= 5;
у2
= 8,
т.е.:
![]() = 0, или 3(х
– 6) + (у
– 5) = 0, т.е. l:
3х
+ у
– 23 = 0.
= 0, или 3(х
– 6) + (у
– 5) = 0, т.е. l:
3х
+ у
– 23 = 0.
Чтобы построить графики прямых l1, l2, l, дополнительно определим по 2 точки для каждой из прямых l1: x – y + 3 = 0, и l2: 5x – 3y – 1 = 0, через которые они проходят. Для этого, задавая, например значение х, по уравнению соответствующей прямой найдем координату у искомой точки:
|
l1: |
х |
0 |
– 3 |
|
l2: |
х |
–1 |
2 |
|
у |
3 |
0 |
|
у |
– 2 |
3 |

Ответ: l: 3х + у – 23 = 0.
3.
Найти расстояние от точки Р(–
4; 2) до прямой
на плоскости:
а) l1:
![]() б)
l2:
б)
l2:
![]() .
.
Решение.
а)
Преобразуем параметрические уравнения
![]() прямойl1
в общее уравнение этой прямой на
плоскости. Для этого исключим из системы
параметр t.
Из 1-го уравнения находим: t
= (х
+ 1)/3. Подставляем это выражение для t
во 2-е уравнение системы: у
= 4(х
+ 1)/3 – 2, откуда получаем: 4х
– 3у
+ 2 = 0.
прямойl1
в общее уравнение этой прямой на
плоскости. Для этого исключим из системы
параметр t.
Из 1-го уравнения находим: t
= (х
+ 1)/3. Подставляем это выражение для t
во 2-е уравнение системы: у
= 4(х
+ 1)/3 – 2, откуда получаем: 4х
– 3у
+ 2 = 0.
Теперь
используем формулу определения расстояние
от точки Р(x0;
y0)
до прямой Ax
+ By
+ C
= 0:
![]() Посколькуx0
= – 4; у0
= 2; А
= 4; В
= – 3; С
= 2, то расстояние от точки Р(–
4; 2) до прямой l1:
Посколькуx0
= – 4; у0
= 2; А
= 4; В
= – 3; С
= 2, то расстояние от точки Р(–
4; 2) до прямой l1:
![]() = 4 лин. ед.
= 4 лин. ед.
б)
Преобразуем каноническое уравнение
![]() прямойl2
в общее уравнение этой прямой на
плоскости: х
– 1 = – 3(у
+ 3), или х
+ 3у
+ 8 = 0.
прямойl2
в общее уравнение этой прямой на
плоскости: х
– 1 = – 3(у
+ 3), или х
+ 3у
+ 8 = 0.
Теперь
используем формулу определения расстояние
от точки Р(x0;
y0)
до прямой Ax
+ By
+ C
= 0:
![]() Посколькуx0
= – 4; у0
= 2; А
= 1; В
= 3; С
= 8, то расстояние от точки Р(–
4; 2) до прямой l2:
Посколькуx0
= – 4; у0
= 2; А
= 1; В
= 3; С
= 8, то расстояние от точки Р(–
4; 2) до прямой l2:
![]() =
=![]() лин. ед.
лин. ед.
Ответ:
а) 4 лин. ед.;
б)
![]() лин. ед.
лин. ед.
4. Даны координаты вершин пирамиды ABCD: A(2; 3; 1), B(4; 1; – 2), C(6; 3; 7), D(– 5; – 4; 8).
Составить:
а) канонические уравнения прямой AB;
б) общее уравнение плоскости ABC;
в) канонические уравнения высоты DO, проведенной из вершины D на основание ABC.
Найти:
г) угол между ребром AD и гранью ABC;
д) длину высоты DO.
Решение.
а) Составляем канонические уравнения прямой AB по координатам двух точек A(2; 3; 1) и B(4; 1; – 2) на этой прямой:
![]() ,
где х1
= 2, у1
= 3, z1
= 1; х2
= 4, у2
= 1, z2
= – 2. Т.о.,
,
где х1
= 2, у1
= 3, z1
= 1; х2
= 4, у2
= 1, z2
= – 2. Т.о.,
АВ:
![]() ,
или
,
или![]() .
.
б)
Составляем общее
уравнение плоскости ABC
по координатам трех точек на этой
плоскости A(2;
3; 1), B(4;
1; – 2), C(6;
3; 7):
 = 0, гдех1
= 2, у1
= 3, z1
= 1; х2
= 4, у2
= 1, z2
= – 2; х3
= 6, у3
= 3, z3
= 7. Т.о., АВС:
= 0, гдех1
= 2, у1
= 3, z1
= 1; х2
= 4, у2
= 1, z2
= – 2; х3
= 6, у3
= 3, z3
= 7. Т.о., АВС:
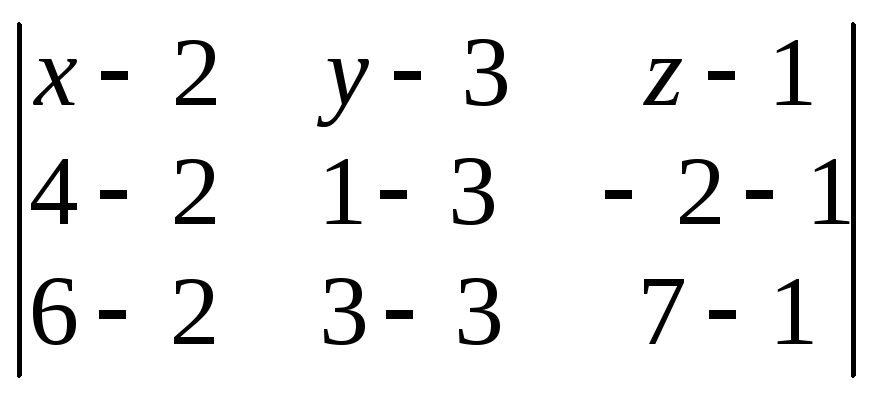 = 0, или,
= 0, или,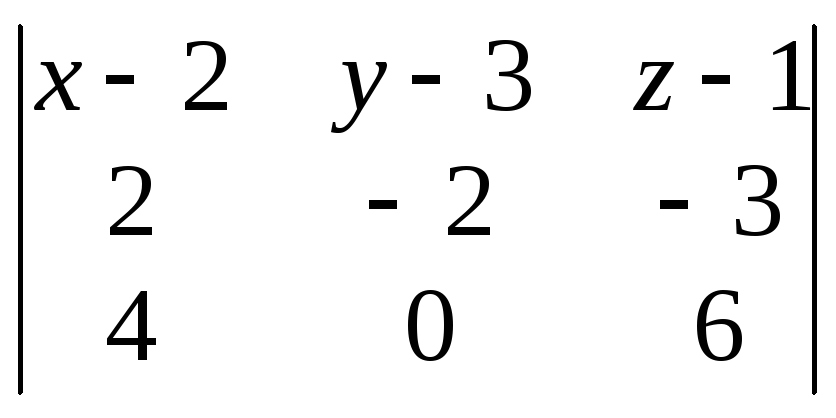 = 0. Разлагая этот определитель по первой
строке, получим: (х
– 2)(–
12) – (у
– 3)24
+ (z
– 1)8
= 0. т.е. уравнением плоскости, содержащей
АВС,
является: – 12х
– 24у +
8z
+ 88 = 0, или 3х
+ 6у –
2z
– 22 = 0.
= 0. Разлагая этот определитель по первой
строке, получим: (х
– 2)(–
12) – (у
– 3)24
+ (z
– 1)8
= 0. т.е. уравнением плоскости, содержащей
АВС,
является: – 12х
– 24у +
8z
+ 88 = 0, или 3х
+ 6у –
2z
– 22 = 0.
в) Перед тем, как составить канонические уравнения прямой DO отметим, что нормальный вектор плоскости АВС N = {3; 6; – 2} является направляющим вектором высоты DO, опущенной из вершины D треугольной пирамиды на ее основание АВС.
Теперь
составляем канонические уравнения
прямой DO
по координатам точки D(–
5; – 4; 8) на этой прямой и направляющему
вектору а
= {3; 6; – 2} этой прямой:
![]() ,
гдех0
= – 5, у0
= – 4, z0
= 8; ах
= 3, ау
= 6, аz
= – 2.
Следовательно, DO:
,
гдех0
= – 5, у0
= – 4, z0
= 8; ах
= 3, ау
= 6, аz
= – 2.
Следовательно, DO:
![]() .
.
г)
Прежде, чем найти угол между ребром AD
и гранью
ABC,
определим канонические уравнения прямой
AD
по координатам точек A(2;
3; 1) и
D(–
5; – 4; 8):
![]() ,
или
,
или![]() ,
или
,
или![]() .
.
Теперь
находим синус острого угла
между ребром AD,
направляющий вектор которого а
= {1; 1; –1}, и
гранью ABC
с нормальным вектором N
= {3; 6; –
2}: sin
=
![]() =
=![]() =
=![]() ≈ 0,9073.
≈ 0,9073.
Следовательно, ≈ arc sin 0,9073 ≈ 65,13.
д)
Находим длину высоты DO,
т.е. расстояние от точки
D(–
5; – 4; 8) до плоскости ABC:
3х
+ 6у –
2z
– 22 = 0. Поскольку расстояние от точки
Р(х0;
у0;
z0)
до плоскости Ax
+ By
+ Cz
+ D
= 0:
![]() ,
то искомая длина высоты DO
равна
,
то искомая длина высоты DO
равна
![]() = 11 лин. ед.
= 11 лин. ед.
Ответ:
а) АВ:
![]() ;
;
б) АВС: 3х + 6у – 2z – 22 = 0;
в)
DO:
![]() ;
;
г) ≈ arc sin 0,9073 ≈ 65,13;
д) 11 лин. ед.
