
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,
Примеры выполнения заданий лабораторной работы
1.
Найти
решение системы двух уравнений
![]() а)
используя формулы Крамера; б)
матричным способом; в)
методом Гаусса.
а)
используя формулы Крамера; б)
матричным способом; в)
методом Гаусса.
Решение.
а) Решение системы по формулам Крамера.
Находим
определитель системы
![]()
= det
A
=
= det
A
=
![]() = – 8 – 15 = – 23.
= – 8 – 15 = – 23.
Находим
дополнительный определитель для
неизвестной х.
Для этого столбец коэффициентов при х
в определителе системы заменяем столбцом
свободных членов системы: 1
=
![]() = – 4 – 65 = – 69.
= – 4 – 65 = – 69.
Находим
дополнительный определитель для
неизвестной y.
Для этого столбец коэффициентов при y
в определителе системы заменяем столбцом
свободных членов системы: 2
=
![]() = 52 – 6 = 46.
= 52 – 6 = 46.
Находим решение системы по формулам Крамера: х = 1/ = – 69/(– 23) = 3; y = 2/ = 46/(– 23) = – 2.
б) Решение системы матричным способом.
Находим
решение системы
![]() в видеX
=
А−1∙B,
где Х
=
в видеX
=
А−1∙B,
где Х
=
![]() ,B
=
,B
=
![]() ,А−1
– обратная матрица к основной матрице
системы А
=
,А−1
– обратная матрица к основной матрице
системы А
=
![]() .
.
Поскольку
(см. справочный материал к 1-й лаб. работе)
для матрицы 2-го порядка А
=
![]() обратная матрицаА
–
1
=
обратная матрицаА
–
1
=
![]()
![]() ,
то получаемА−1
=
,
то получаемА−1
=
![]() =
=![]() .
.
Т.о.,
Х
=
![]() =
=![]()
![]() =
=![]() =
=![]() .
Следовательно,х
= 3; y
= – 2.
.
Следовательно,х
= 3; y
= – 2.
в) Решение системы методом Гаусса.
Выполняем
прямой ход метода Гаусса, т.е. приводим
расширенную матрицу системы (А|B)
=
![]() к ступенчатому виду. Для этого в качестве
ведущего элемента берем в 1-м столбце
матрицыА
1-й диагональный элемент, равный 4, и
элементарными преобразованиями строк
расширенной матрицы зануляем нижестоящий
элемент в этом столбце:
к ступенчатому виду. Для этого в качестве
ведущего элемента берем в 1-м столбце
матрицыА
1-й диагональный элемент, равный 4, и
элементарными преобразованиями строк
расширенной матрицы зануляем нижестоящий
элемент в этом столбце:
стр.:
4II–3∙I
![]() ~
~
![]() .
.
В результате получаем систему, равносильную исходной:
![]()
Выполняем обратный ход метода Гаусса: из последнего уравнения находим y = – 2, и подставляем полученное значение в вышестоящее уравнение: 4х + 5(–2) = 2, откуда находим: 4х = 2 + 10 = 12, т.е. х = 3.
Ответ: х = 3; y = – 2.
2.
Найти
решение системы трех уравнений
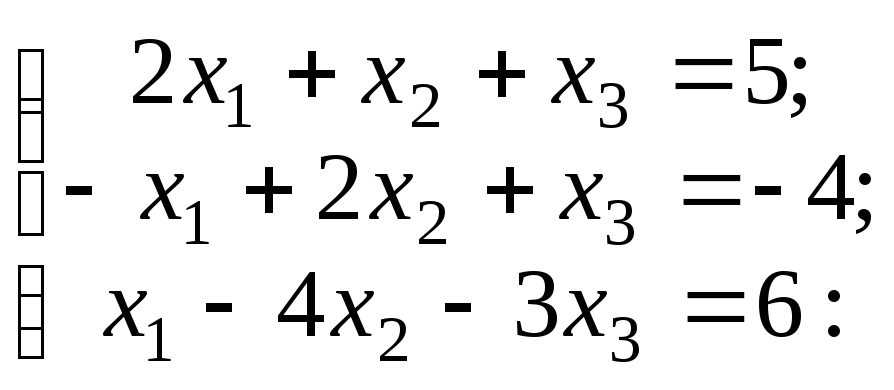 а)
используя формулы Крамера; б)
матричным способом; в)
методом Гаусса.
а)
используя формулы Крамера; б)
матричным способом; в)
методом Гаусса.
Решение.
а) Решение системы по формулам Крамера.
Находим
определитель системы
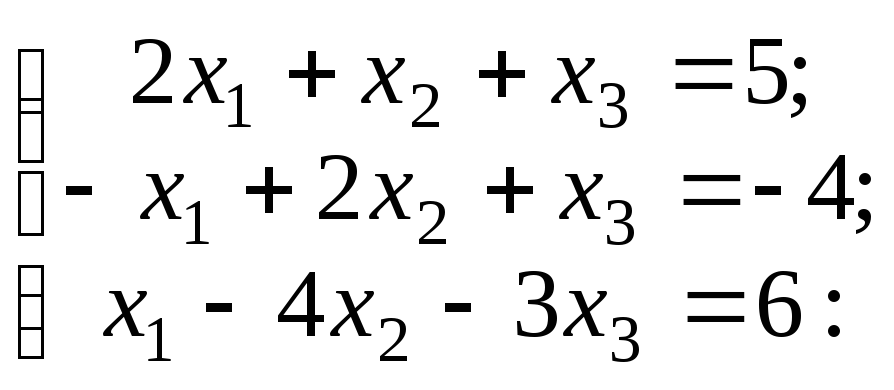
= det
A
=
= det
A
=
 = – 12 +4 +1 – 2 +8 – 3 = – 4.
= – 12 +4 +1 – 2 +8 – 3 = – 4.
Находим
дополнительный определитель для
неизвестной х1.
Для этого столбец коэффициентов при х1
в определителе системы заменяем столбцом
свободных членов системы: 1
=
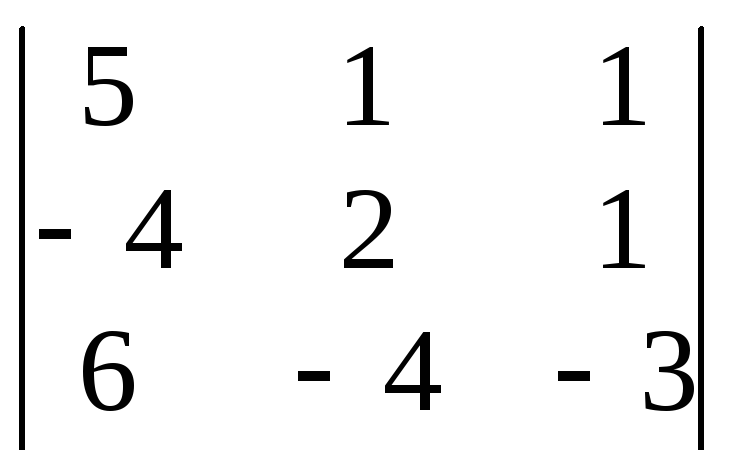 = – 30 + 16 + 6 – 12 + 20 – 12 = – 12.
= – 30 + 16 + 6 – 12 + 20 – 12 = – 12.
Находим
дополнительный определитель для
неизвестной х2.
Для этого столбец коэффициентов при х2
в определителе системы заменяем столбцом
свободных членов системы: 2
=
 = 24 – 6 + 5 + 4 – 12 – 15 = 0.
= 24 – 6 + 5 + 4 – 12 – 15 = 0.
Находим
дополнительный определитель для
неизвестной х3.
Для этого столбец коэффициентов при х3
в определителе системы заменяем столбцом
свободных членов системы: 3
=
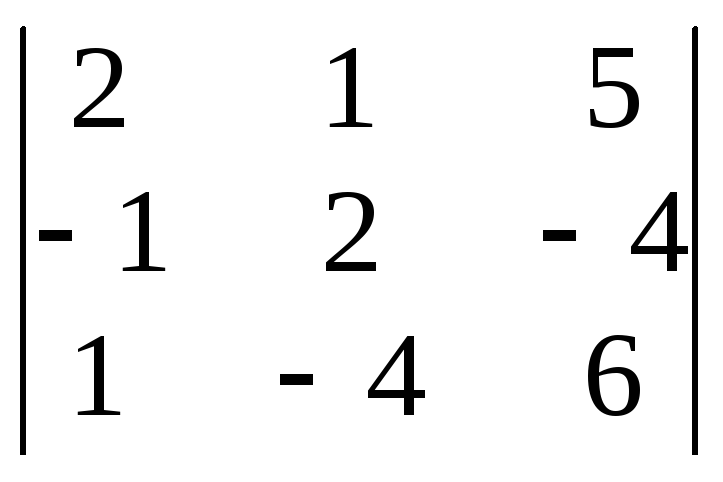 = 24 + 20 – 4 – 10 – 32 + 6 = 4.
= 24 + 20 – 4 – 10 – 32 + 6 = 4.
Находим решение системы по формулам Крамера: х1 = 1/ = – 12/(– 4) = 3; х2 = 2/ = 0/(– 4) = 0; х3 = 3/ = 4/(– 4) = – 1.
б) Решение системы матричным способом.
Находим
решение системы
 в видеX
=
А−1∙B,
где Х
=
в видеX
=
А−1∙B,
где Х
=![]() ,B
=
,B
=![]() ,А−1
– обратная матрица к основной матрице
системы А
=
,А−1
– обратная матрица к основной матрице
системы А
=
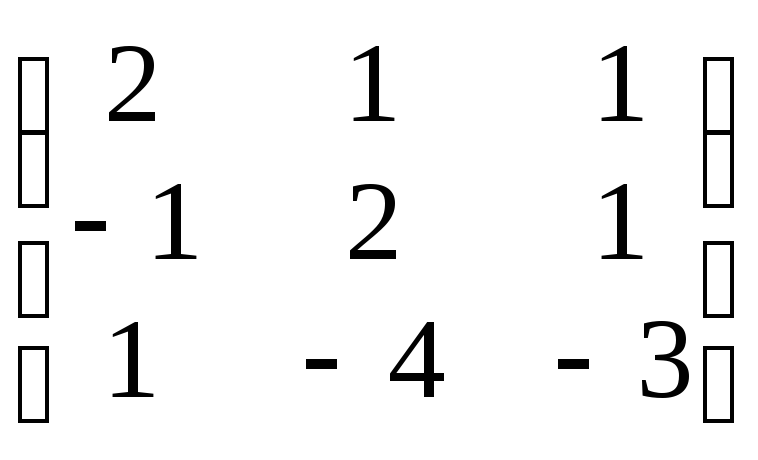 .
.
Находим обратную матрицу А−1 матричным методом:
стр.:
II–I
стр.:
III+3∙I
стр.:
I+III
стр.:
II+III
(А|Е)
=
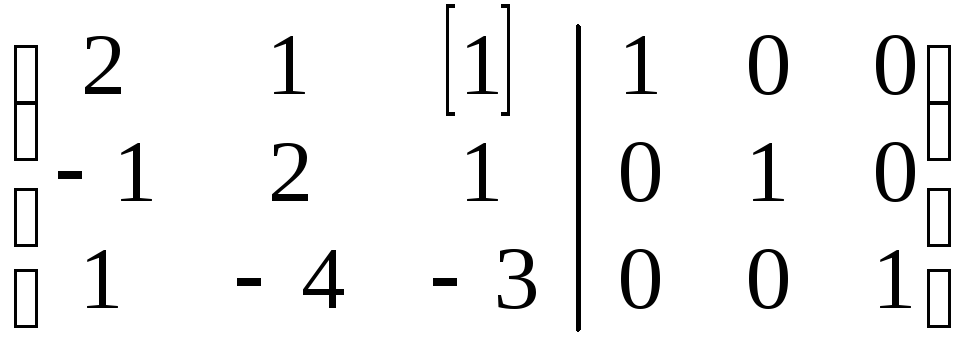 ~
~
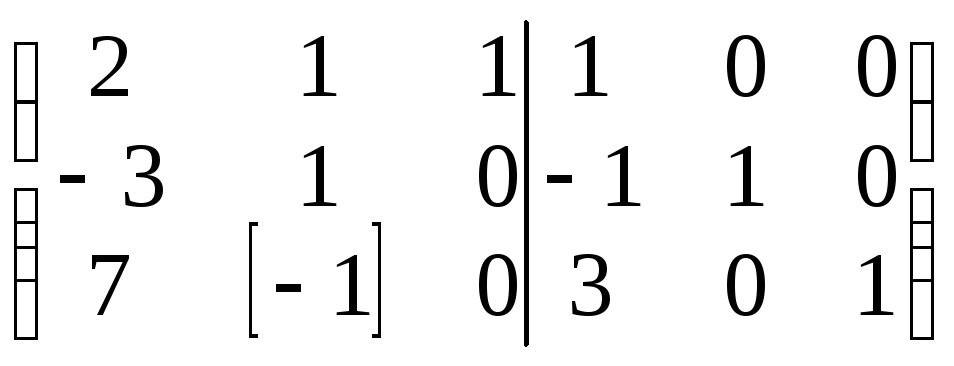 ~
~
стр.:
I/4
стр.:
II/4
стр.:
III/(–4)
стр.:
4I–9II
стр.:
4III–7∙II
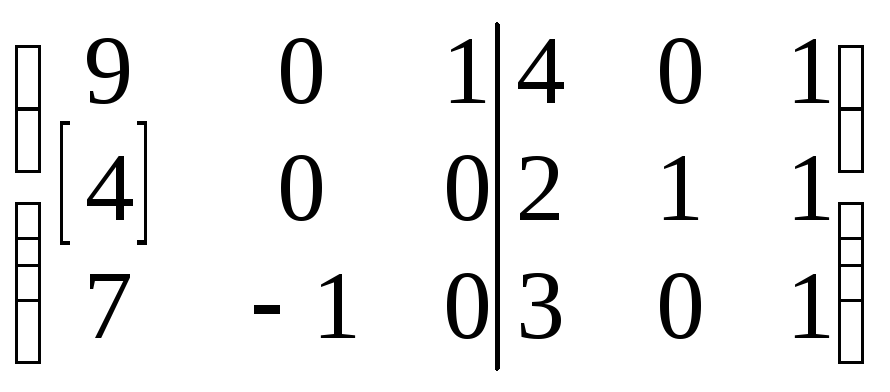 ~
~
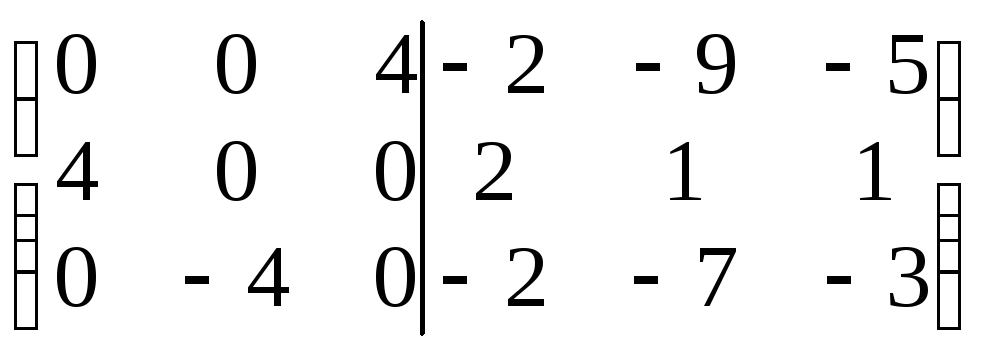 ~
~
Перестановка
строк
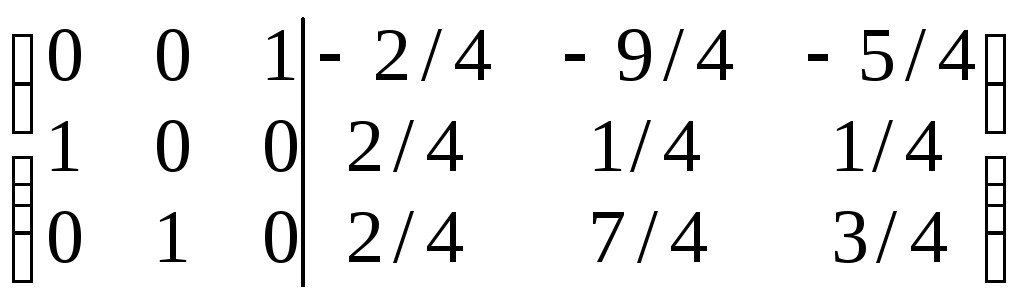 ~
~
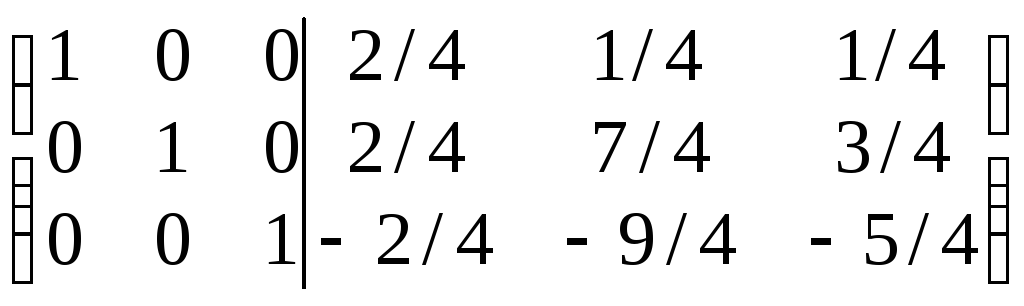 = (E|A–1).
= (E|A–1).
Следовательно,
A–1
=
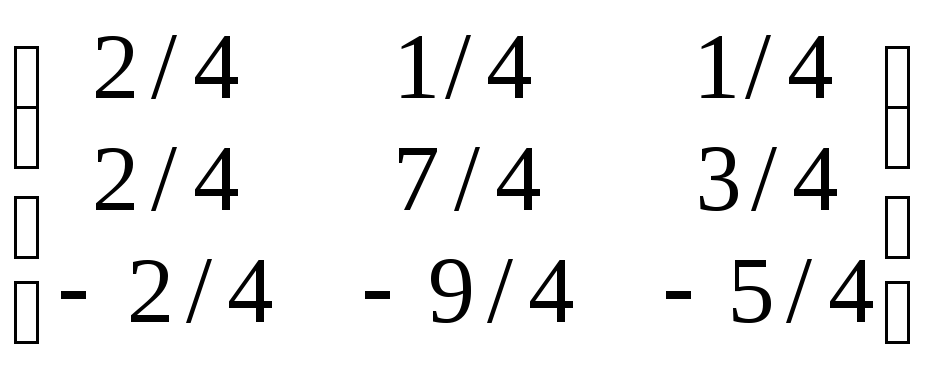 =
= .
.
Т.о.,
Х
=
![]() =
=
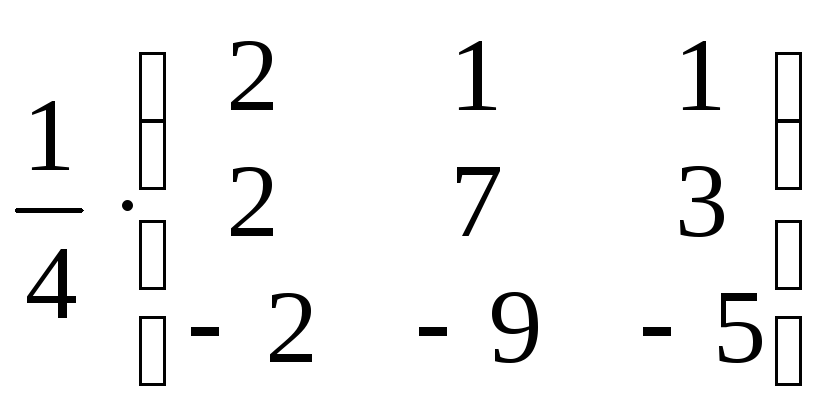
![]() =
=
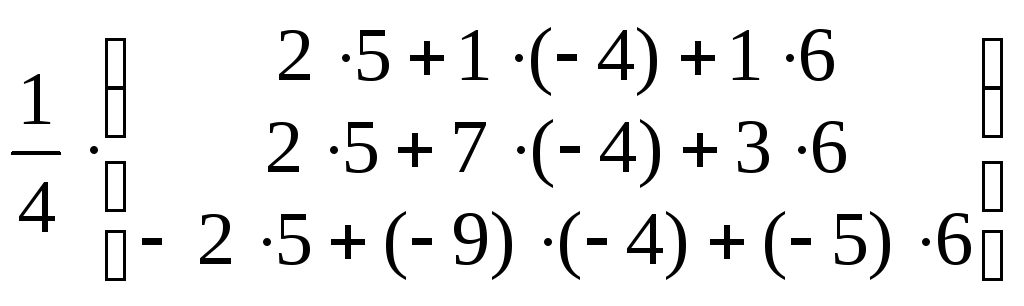 =
=
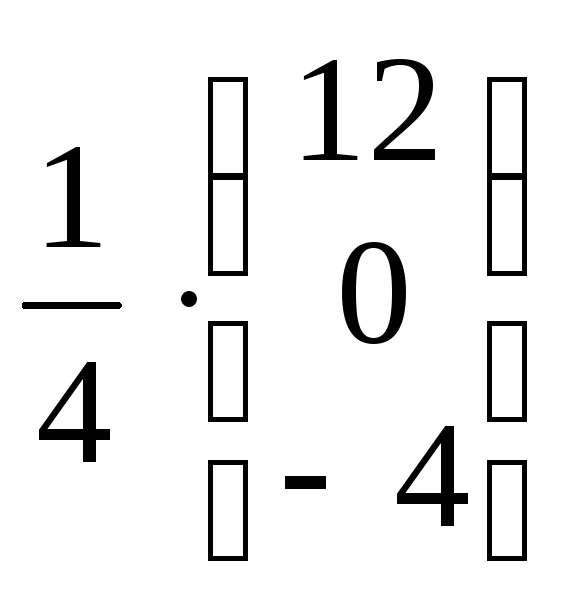 =
=
![]() .
.
Следовательно, х1 = 3; х2 = 0; х3 = – 1.
в) Решение системы методом Гаусса.
Выполняем
прямой ход метода Гаусса, т.е. приводим
расширенную матрицу системы (А|B)
=
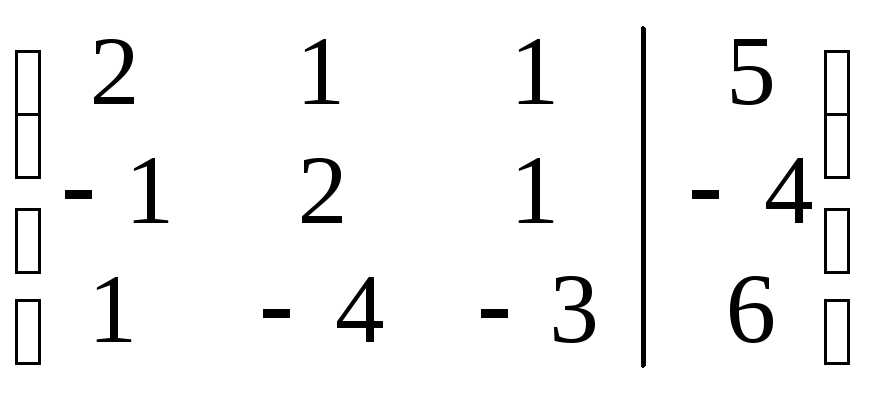 к ступенчатому виду. Для этого
последовательно слева направо в качестве
ведущих элементов берем диагональные
элементы преобразуемой матрицыА
и элементарными преобразованиями строк
расширенной матрицы зануляем нижестоящие
элементы в соответствующих столбцах
(т.е. последовательно исключаем неизвестные
из ниже находящихся уравнений системы
относительно верхних уравнений):
к ступенчатому виду. Для этого
последовательно слева направо в качестве
ведущих элементов берем диагональные
элементы преобразуемой матрицыА
и элементарными преобразованиями строк
расширенной матрицы зануляем нижестоящие
элементы в соответствующих столбцах
(т.е. последовательно исключаем неизвестные
из ниже находящихся уравнений системы
относительно верхних уравнений):
стр.:
2II+I
стр.:
2III–I
стр.:
5III+9II
 ~
~
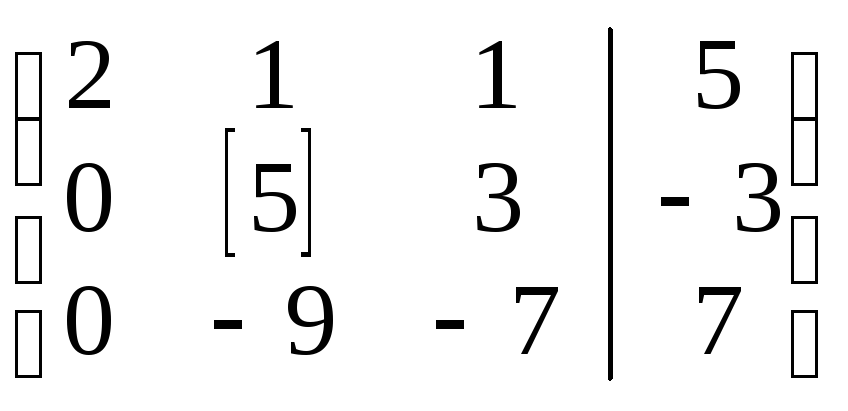 ~
~
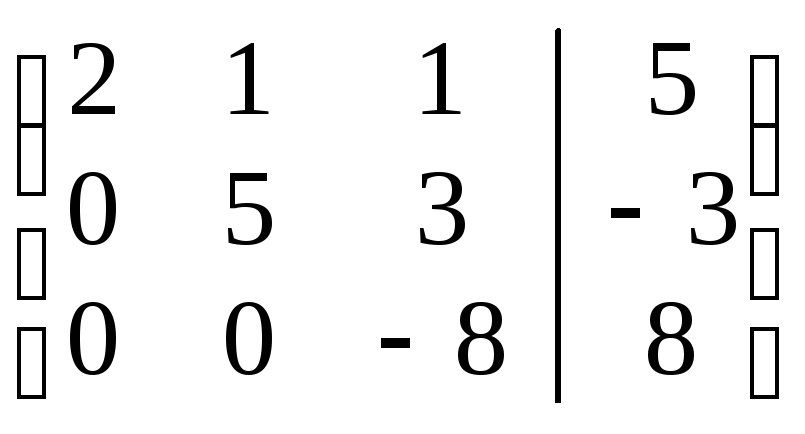 .
.
В результате получаем систему, равносильную исходной:
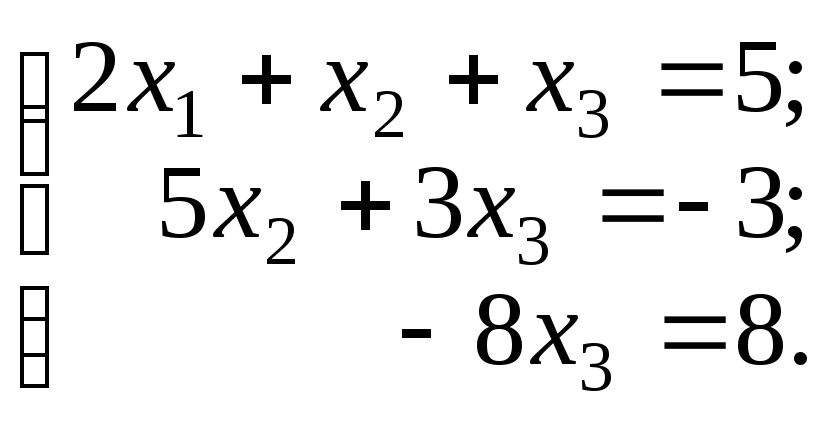
Выполняем обратный ход метода Гаусса.
Из последнего уравнения находим х3 = – 1.
Подставляем полученное значение х3 в вышестоящее уравнение: 5х2 + 3(–1) = –3, откуда находим: 5х2 = – 3 + 3 = 0, т.е. х2 = 0.
Подставляем полученные значения х2 и х3 в первое уравнение системы: 2х1 + 0 + (–1) = 5, откуда 2х1 = 6, т.е. х1 = 3.
Ответ: х1 = 3; х2 = 0; х3 = – 1.
2.
Используя
метод Гаусса, найти общее и базисное
решения системы линейных уравнений:
а)
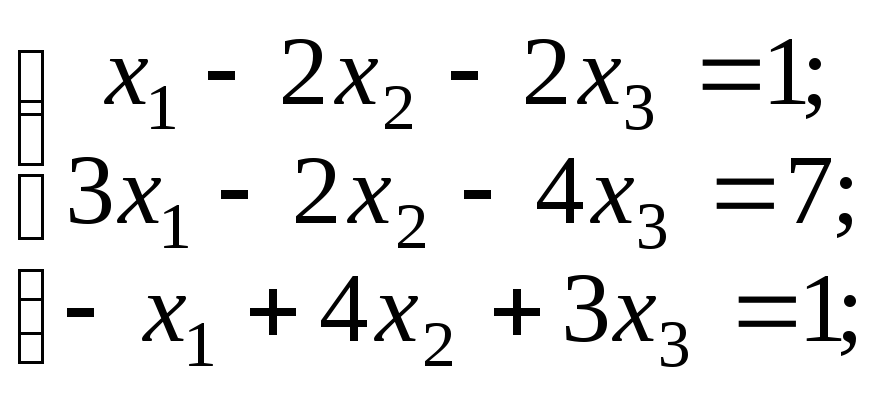 б)
б)
 в)
в)
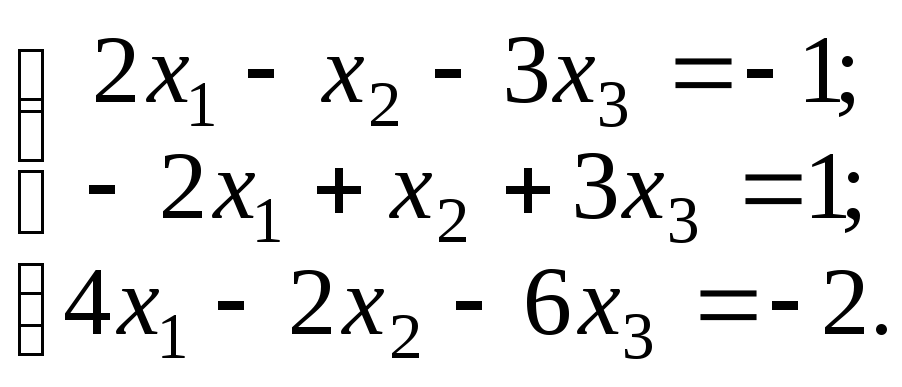
Решение.
а)
Составляем
расширенную матрицу системы:
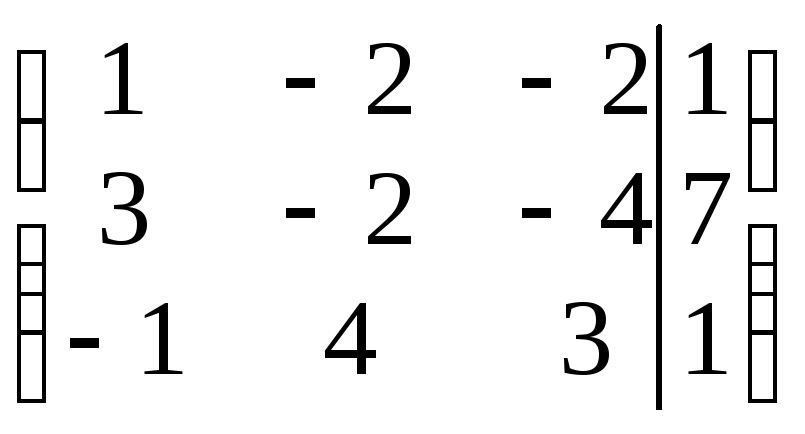 .
.
Выполняем прямой ход метода Гаусса: элементарными преобразованиями строк расширенной матрицы приводим ее к ступенчатому виду:
стр.:
II−3∙I
стр.:
III+I
стр.:
II ∕
2
стр.:
III−II
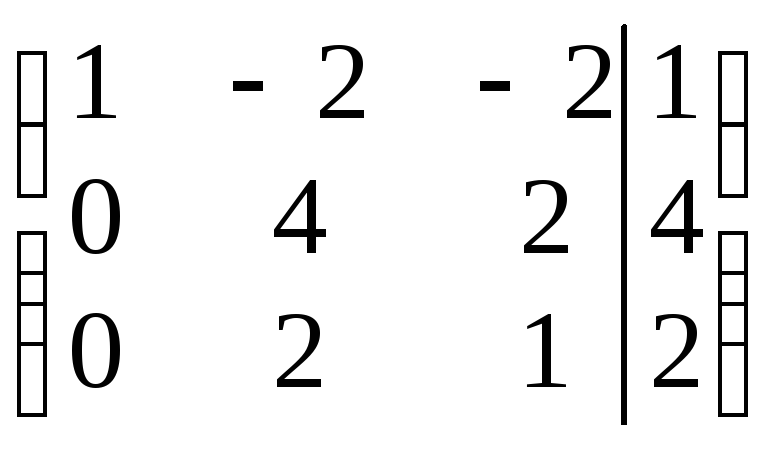 ~
~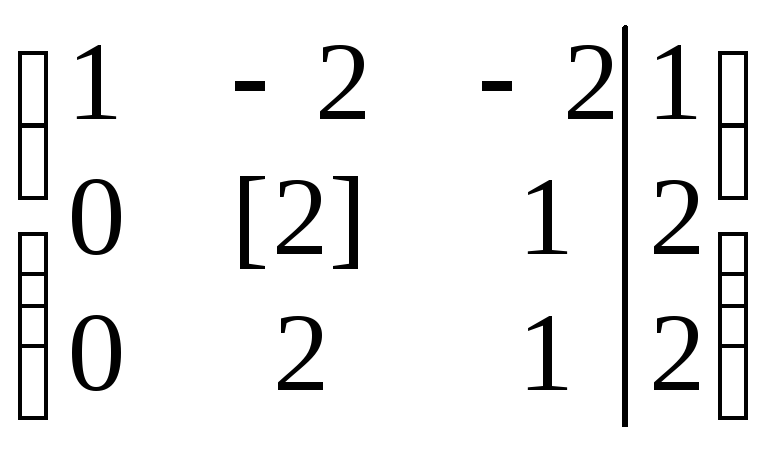 ~
~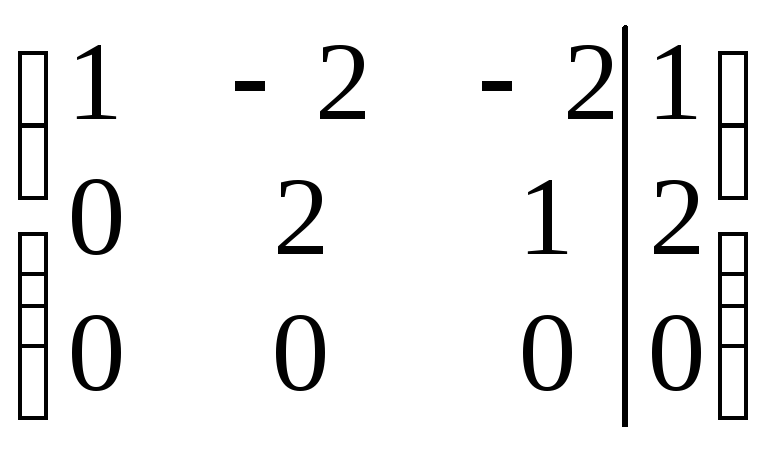 .
.
По полученной расширенной матрице ступенчатого вида системы запишем систему уравнений, равносильную исходной:
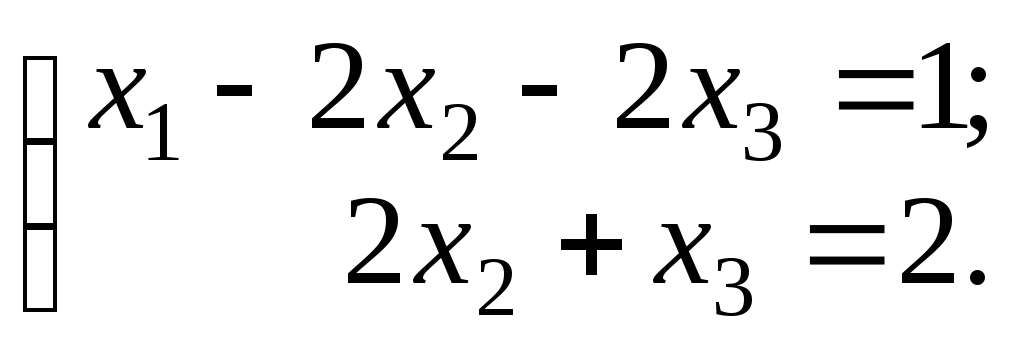
В полученной системе 2 уравнения и 3 неизвестных, следовательно, в исходной системе 2 базисных неизвестных и одна свободная. В качестве базисных неизвестных возьмем x1 и x2, что допустимо, поскольку соответствующие им коэффициенты в расширенной матрице ступенчатого вида без нулевых строк образуют диагональную матрицу, определитель которой отличен от нуля.
Базисные неизвестные оставим в левой части уравнений, а свободную неизвестную x3 в качестве параметра переносим в правую часть уравнений:
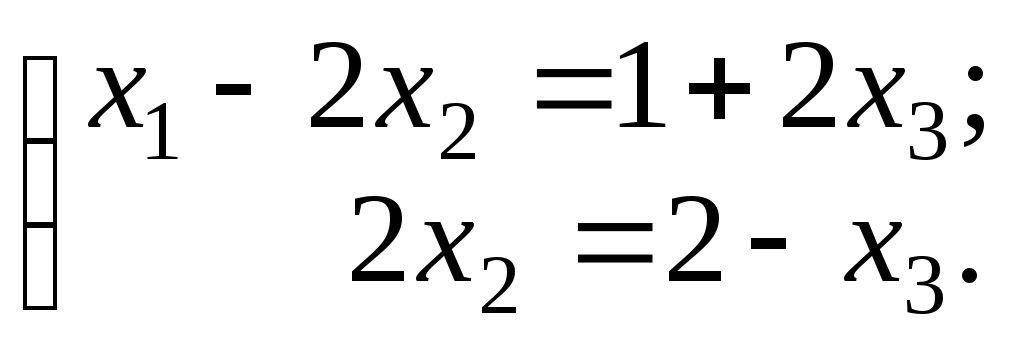
Выполняем обратный ход метода Гаусса: найдем общее решение системы последовательным вычислением значений базисных неизвестных путем перехода от нижнего уравнения к верхнему.
Из второго уравнения определяется x2 = 1 − x3 / 2. Подставляя это значение в первое уравнение, получим x1 = 1 + 2x3 + 2∙(1 − x3 / 2) = 3 + x3.
Чтобы подчеркнуть, что x3 как параметр может принимать любые числовые значения, а также чтобы избавиться в ответе от дробей, переобозначим свободную неизвестную: x3 = 2С, где С – произвольная константа.
С
учетом произведенной замены запишем
общее решение в виде вектора-столбца
X
=
![]() =
=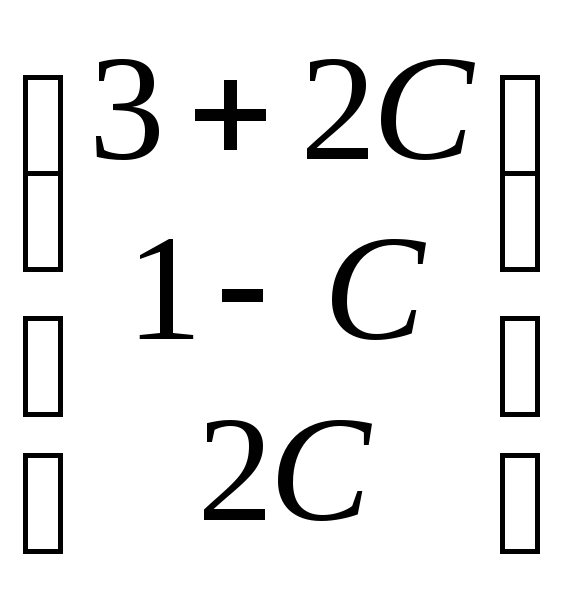 .
.
Запишем базисное решение, получаемое при равенстве всех свободных неизвестных нулю (в нашем случае x3 = 0 и, следовательно, С = 0):
X0
=
![]() .
.
Ответ: общее решение системы x1 = 3 + 2С, x2 = 1 − С, x3 = 2С;
базисное решение системы x1 = 3, x2 = 1, x3 = 0.
б)
Составляем
расширенную матрицу системы:
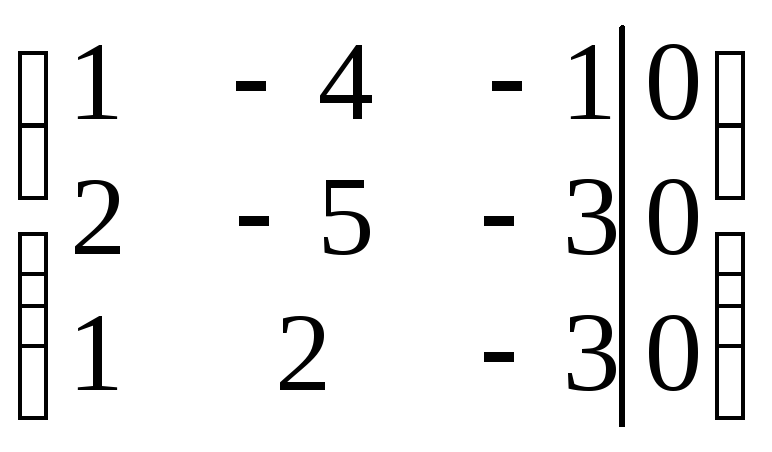 .
.
Выполняем прямой ход метода Гаусса: элементарными преобразованиями строк расширенной матрицы приводим ее к ступенчатому виду:
стр.:
II−2∙I
стр.:
III−I
стр.:
III−2∙II
 ~
~
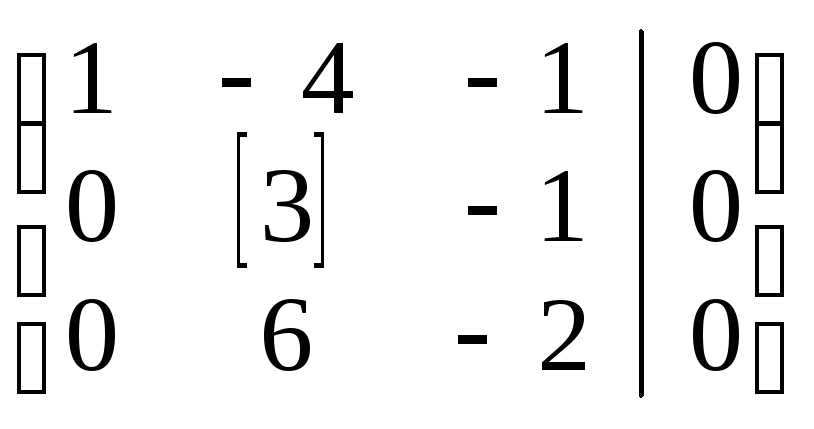 ~
~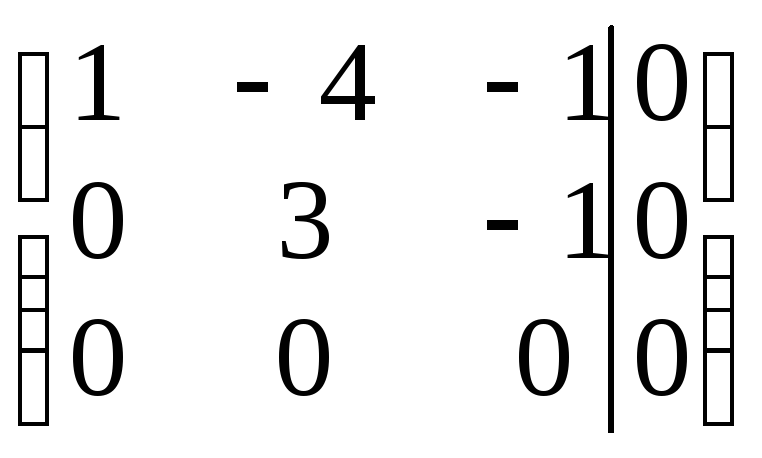 .
.
По
полученной расширенной матрице
ступенчатого вида системы запишем
систему уравнений, равносильную исходной:

В полученной системе 2 уравнения и 3 неизвестных, следовательно, в исходной системе 2 базисных неизвестных и одна свободная. В качестве базисных неизвестных возьмем x1 и x2, что допустимо, поскольку соответствующие им коэффициенты в расширенной матрице ступенчатого вида без нулевых строк образуют диагональную матрицу, определитель которой отличен от нуля.
Базисные
неизвестные оставим в левой части
уравнений, а свободную неизвестную x3
в качестве параметра переносим в правую
часть уравнений:
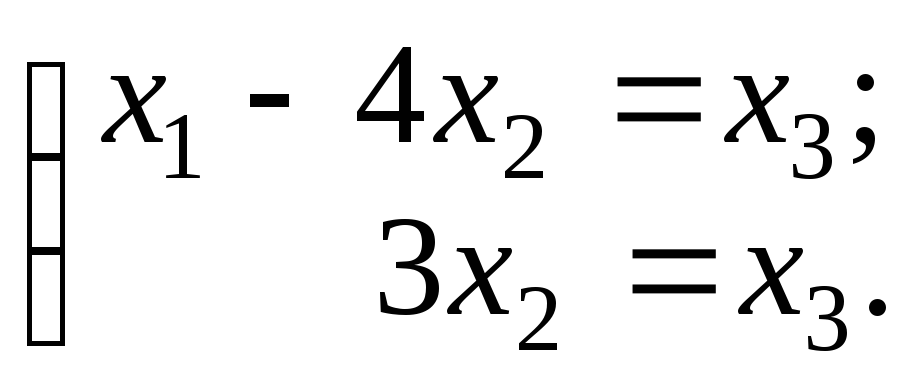
Выполняем обратный ход метода Гаусса: найдем общее решение системы последовательным вычислением значений базисных неизвестных путем перехода от нижнего уравнения к верхнему.
Из второго уравнения определяется x2 = x3 / 3. Подставляя это значение в первое уравнение, получим x1= x3 + 4x3 / 3 = 7x3 / 3.
Чтобы подчеркнуть, что x3 как параметр может принимать любые числовые значения, а также чтобы избавиться в ответе от дробей, переобозначим свободную неизвестную: x3 = 3С, где С – произвольная константа.
С учетом произведенной замены запишем общее решение в виде вектора-столбца
X
=
![]() =
=![]() =C∙
=C∙![]() .
.
Запишем базисное решение, получаемое при равенстве всех свободных неизвестных нулю (в нашем случае x3 = 0 и, следовательно, С = 0):
X0
=
![]() .
.
Ответ: общее решение системы: x1 = 7С, x2 = С, x3 = 3С;
базисное решение системы: x1 = 0, x2 = 0, x3 = 0.
в)
Составляем расширенную матрицу системы:
 .
.
Выполняем прямой ход метода Гаусса: элементарными преобразованиями строк расширенной матрицы приводим ее к ступенчатому виду:
стр.:
II+I
стр.:
III−2∙I
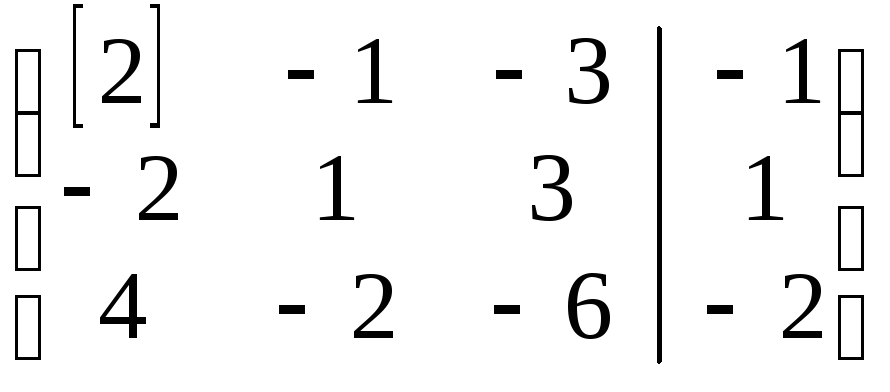 ~
~
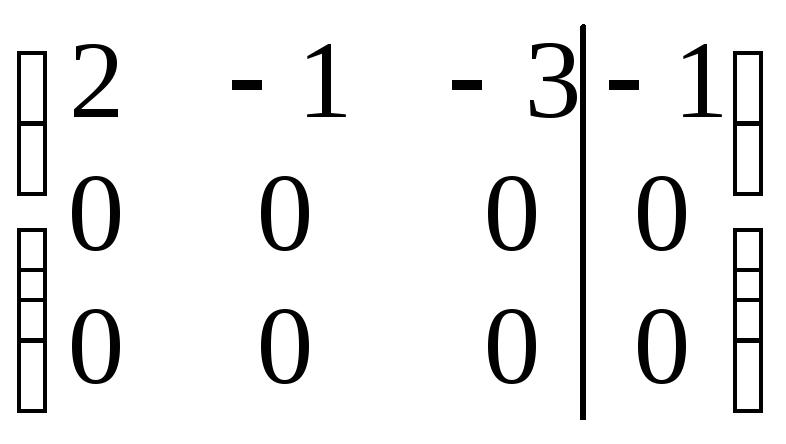 .
.
Согласно полученной расширенной матрице исходная система сводится к единственному уравнению
2∙x1 − x2 − 3∙x3 = −1.
Поскольку в полученном единственном уравнении 3 неизвестных, то в исходной системе одна базисная неизвестная и 2 свободные. В качестве базисной неизвестной выбираем x1.
Базисную неизвестную оставим в левой части уравнений, а свободные неизвестные x2 и x3 в качестве параметров переносим в правую часть уравнения:
2∙x1 = −1 + x2 + 3∙x3, откуда x1 = −1/ 2 + x2 / 2 + 3∙x3 / 2.
Запишем общее решение системы, переобозначив свободные неизвестные: x2 = 2∙С1, x3 = 2∙С2, где С1 и С2 – произвольные константы:
x1 = −1/ 2 + С1 + 3∙С2.
С учетом произведенной замены запишем общее решение в виде вектора-столбца
X
=
![]() =
=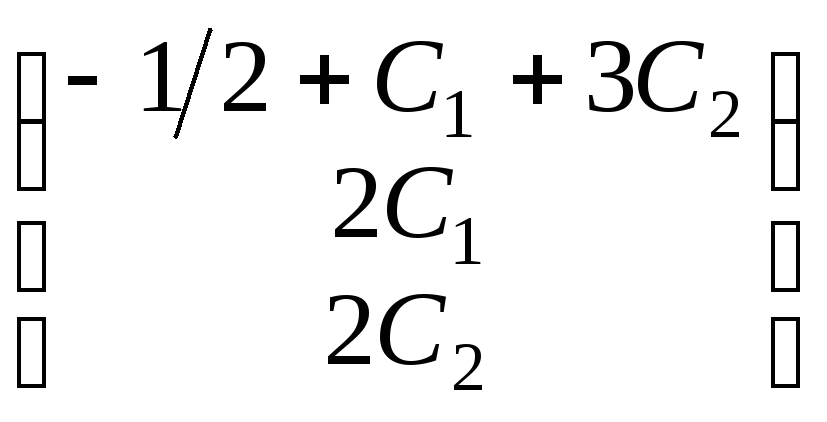 .
.
Запишем базисное решение, получаемое при равенстве всех свободных неизвестных нулю (в нашем случае x2 = 0, x3 = 0 и, следовательно, С1 = С2 = 0):
X0
=
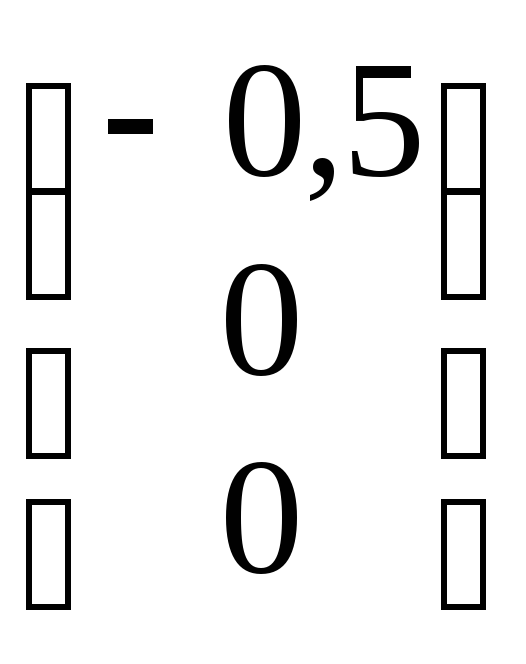 .
.
Ответ: общее решение системы x1 = − 0,5 + С1 + 3С2; x2 = 2С1; x3 = 2С2;
базисное решение системы x1 = − 0,5; x2 = 0; x3 = 0.
Примечание:
если
исходная
система
в задании 3в
имела бы, например, вид
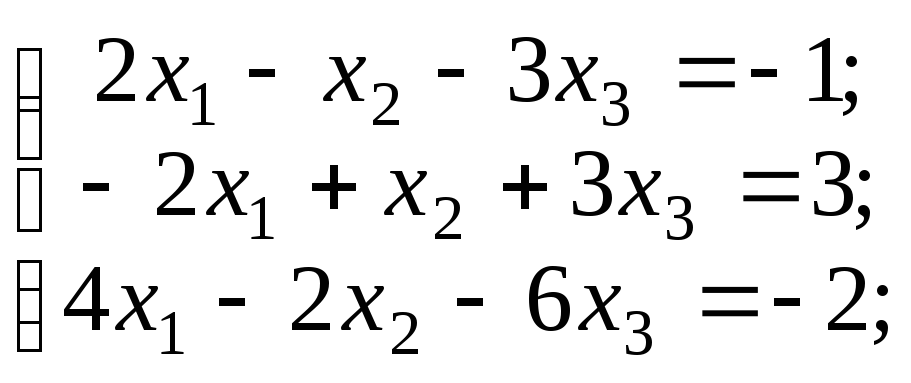 то получится соответствующая этой
системе расширенная матрица ступенчатого
вида:
то получится соответствующая этой
системе расширенная матрица ступенчатого
вида: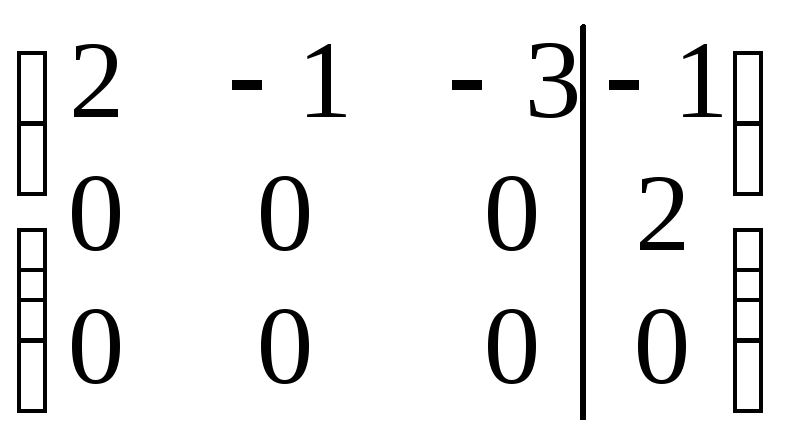 .
Следовательно, для такой системы ранг
основной матрицы (rang
A
= 1) не равен рангу расширенной матрицы
(rang
(A|B)
= 2), и поэтому она несовместна, т.е. решений
не имеет.
.
Следовательно, для такой системы ранг
основной матрицы (rang
A
= 1) не равен рангу расширенной матрицы
(rang
(A|B)
= 2), и поэтому она несовместна, т.е. решений
не имеет.
