Справочный материал

к 8-й лабораторной работе

1. Производная функции у = у(х) по переменной х в точке х₀ – конечный двусторонний предел отношения изменения значения функции у = у(х) к соответствующему бесконечно малому изменению значения аргумента х этой функции в окрестности точки х = х₀: у (х₀) = 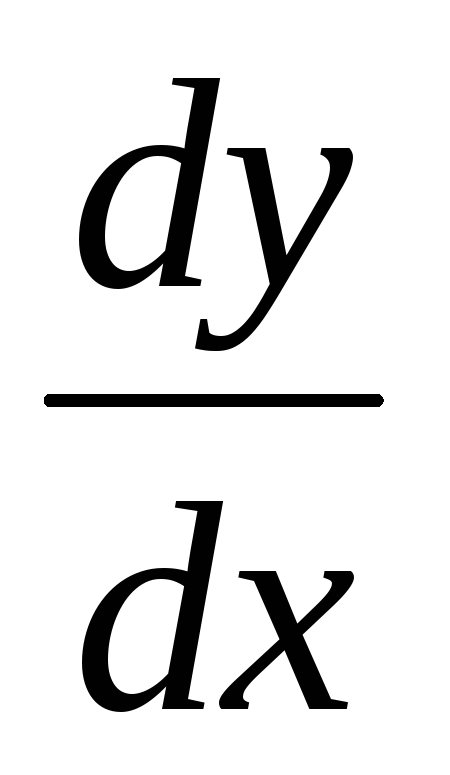===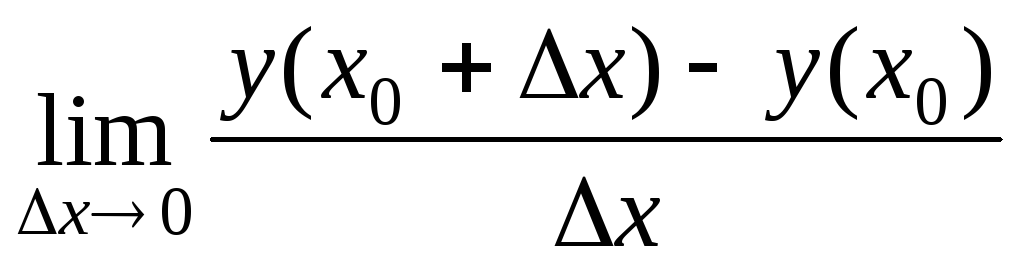. Значение производнойу (х₀) равно тангенсу угла наклона касательной к графику функции у = у(х) при х = х₀ относительно положительного направления координатной оси х. Если s(t) – зависимость перемещения материальной точки от времени, то s (t) = =v(t) – мгновенная скорость этой материальной точки в момент времени t.

2. Дифференцируемость функции у = у(х): если в каждой точке х интервала (а; b) существует производная у(х), то функция у = у(х) называется дифференцируемой на этом интервале.

3. Правила дифференцирования – производная алгебраической суммы: (u  v) = u  v ; (u  v  w) = u  v  w ; производная произведения: (uv) = uv + uv; (uvw) = uvw + uvw + uvw ; производная дроби: (u/ v) = (uv – uv )/ v².

4. Производная параметрически заданной функции x = x(t), y = y(t): y (x) = y (t) / x (t).

5. Производная сложной функции: если y = u(v(w(x))), то= 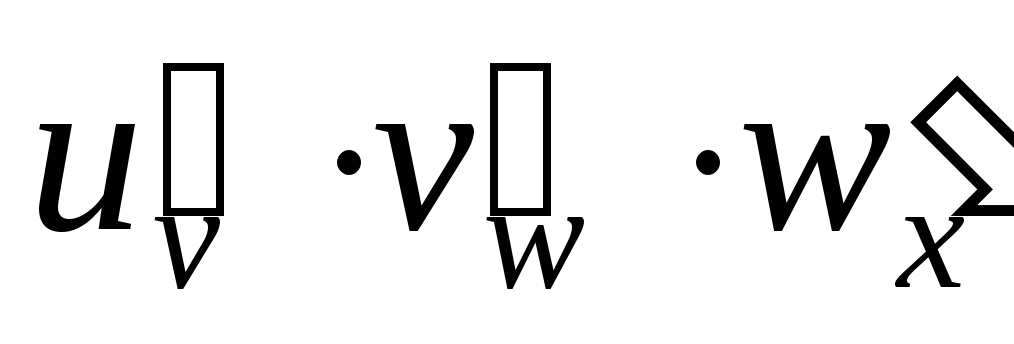. Последовательность дифференцирования сложной функции обратна последовательности вычисления значения функции, в частности, на калькуляторе. Например, при вычислении значения функцииу = sin²(ln(x³+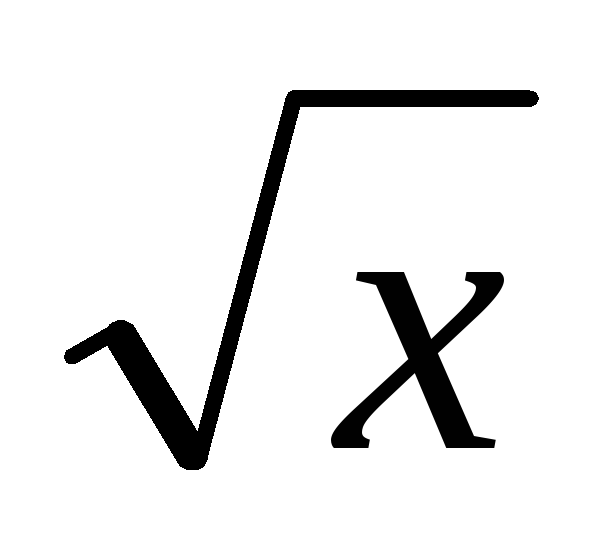)) в точке х алгебраические операции выполняются в следующей последовательности: куб х, квадратный корень из х, сумма куба и квадратного корня, логарифм суммы, синус логарифма, квадрат синуса, следовательно, нахождение производной у (х) сводится к произведению производных, определяемых в последовательности: производная квадрата синуса, производная синуса логарифма, производная логарифма суммы, производная суммы, равная сумме производных куба х и квадратного корня из х, т.е. каждая следующая дифференцируемая функция является аргументом предыдущей.

6. Таблица производных основных элементарных функций

Вид функции	Формула функции	Производная функции
1) Постоянная	y = C для всех х 	С = 0
2) Линейная	y = х, х y = ах  b, х	х = 1 (ах  b) = а
3) Степенная	y = х^а, х > 0, а  y = х ^– а, х > 0, а  y = 1/х, х  0 , х > 0 , х > 0, n \{1}	(х^а) = ах^а –^1 (х^– а) = –ах ^– а –^1 (1/х) = –1/x^2 () = 1/() () = 1/()
4) Показательная	y = а^х, а > 0, а  1, х  y = е^х, х  y = е^– х, х 	(а^х) = а^хln а (е^х) = е^х (е^– х) = – е^– х
5) Показательно-степенная	y = u(х)^v^(^х^)	(u^v)=(vu^v–^1)u+(u^vln u)v
6) Логарифмическая	y = log ах, а > 0, а  1, х > 0 y = lnх, х > 0	(log ах) = 1/(xln a) (lnх) = 1/х
7) Тригонометрическая	y = sin x х  y = cos x х  y = tg x х  y = ctg x х 	(sin x) = cos x (cos x) = – sin x (tg x) = 1/cos^2x (ctg x) = – 1/sin^2 x
8) Обратная тригонометрическая	y = arc sin x –1  х  1 y = arc cos x –1  х  1 y = arc tg x х  y = arc ctg x х 	(arc sin x) = 1/ (arc cos x) = – 1/ (arc tg x) = 1/(1 + x^2) (arc ctg x) = – 1/(1 + x^2)
9) Гиперболическая	y = sh x х  y = ch x х  y = th x х  y = cth x х  0	(sh x) = ch x (ch x) = sh x (th x) = 1/ch^2x (cth x) = – 1/sh^2 x

7. _{Уравнение касательной к кривой у = у(х) в точке} М(х₀; у₀), где y_{0 =} y(x₀): y = y₀ + _у'(х0)(x – x₀).

8. Уравнение нормали к кривой _{у = у(х) в точке} М(х₀; у₀): y = y₀ –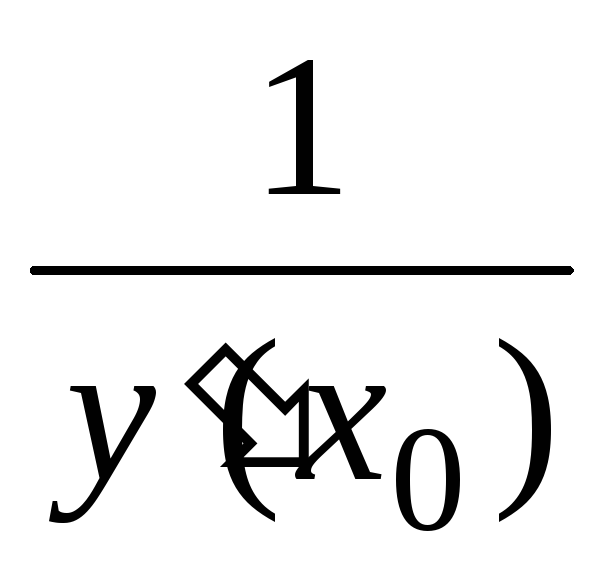(x – x₀).

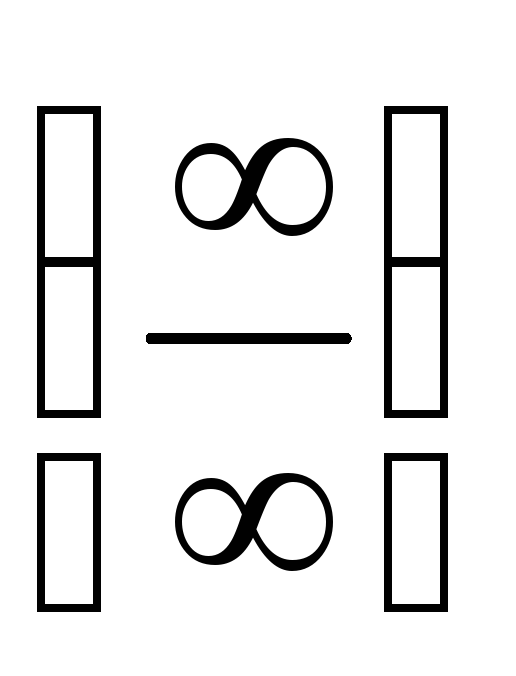9. Правило Лопиталя: _{= , где а – любое конечное число или ∞. Правило Лопиталя можно использовать только для неопределенностей вида} и. _{Правило Лопиталя можно использовать многократно, если при его использовании снова возникает одна из указанных неопределенностей.}