
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,
Примеры выполнения заданий лабораторной работы
1. Вычислить пределы функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;г)
;г)
![]() ;д)
;д)
![]() ;е)
;е)
![]() ;
ж)
;
ж)
![]() ;з)
;з)
![]() ;
и)
;
и)
![]() .
.
Решение.
а)
Подставляем
в функцию предельное значение переменной
х
= 4:
![]() =
=
![]() =
=![]() =
=![]() .
.
б)
Подставляем
в функцию предельное значение переменной
х
= :
за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Поскольку и в числителе и в знаменателе
дроби имеем многочлены, а предел находится
прих
,
то в каждом из этих многочленов оставляем
член с х
в максимальной степени:
.
Поскольку и в числителе и в знаменателе
дроби имеем многочлены, а предел находится
прих
,
то в каждом из этих многочленов оставляем
член с х
в максимальной степени:
![]() =
=
![]() =
=
![]() = 2.
= 2.
в)
Подставляем
в функцию предельное значение переменной
х
= 0: за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Поскольку и в числителе и в знаменателе
дроби имеем многочлены, а предел находится
прих
0, то в каждом из этих многочленов
оставляем член с х
в
минимальной степени:
.
Поскольку и в числителе и в знаменателе
дроби имеем многочлены, а предел находится
прих
0, то в каждом из этих многочленов
оставляем член с х
в
минимальной степени:
![]() =
=![]() =
=![]() = – 3.
= – 3.
г)
Подставляем
в функцию предельное значение переменной
х
= 2: за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Поскольку и в числителе и в знаменателе
дроби многочлены, а предел находится
прих
2, то в этих многочленах выделяем
бесконечную малую (х
–
2): корнями многочлена числителя являются
х1
= 2, х2
= 1/2, поэтому
.
Поскольку и в числителе и в знаменателе
дроби многочлены, а предел находится
прих
2, то в этих многочленах выделяем
бесконечную малую (х
–
2): корнями многочлена числителя являются
х1
= 2, х2
= 1/2, поэтому
![]() =
=
![]() =
=
![]() =
=![]() = 3/4.
= 3/4.
д )
Подставляем
в функцию предельное значение переменной
х
= 0: за знаком предела
)
Подставляем
в функцию предельное значение переменной
х
= 0: за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Поскольку в числителе разность корней,
то переносим иррациональность в
знаменатель, умножив и числитель, и
знаменатель на соответствующую сумму
корней:
.
Поскольку в числителе разность корней,
то переносим иррациональность в
знаменатель, умножив и числитель, и
знаменатель на соответствующую сумму
корней:
![]() =
=![]() =
=
![]() =
=![]() =
=![]() =
=![]() .
.
е)
Подставляем
в функцию предельное значение переменной
х
= 0: за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Для раскрытия неопределенности
воспользуемся эквивалентными малыми.
Поскольку в окрестности точких
= 0: 1 – cos
α(х)
~ 2(х)/2,
tg
α(х)
~ α(х),
arcsin
α(х)
~ α(х),
то 1 – cos
х
~ х2/2,
сtg
3х2=
1/tg
3x2
~ 1/(3х2),
arcsin3х
~ х3.
.
Для раскрытия неопределенности
воспользуемся эквивалентными малыми.
Поскольку в окрестности точких
= 0: 1 – cos
α(х)
~ 2(х)/2,
tg
α(х)
~ α(х),
arcsin
α(х)
~ α(х),
то 1 – cos
х
~ х2/2,
сtg
3х2=
1/tg
3x2
~ 1/(3х2),
arcsin3х
~ х3.
Получаем:
![]() =
=
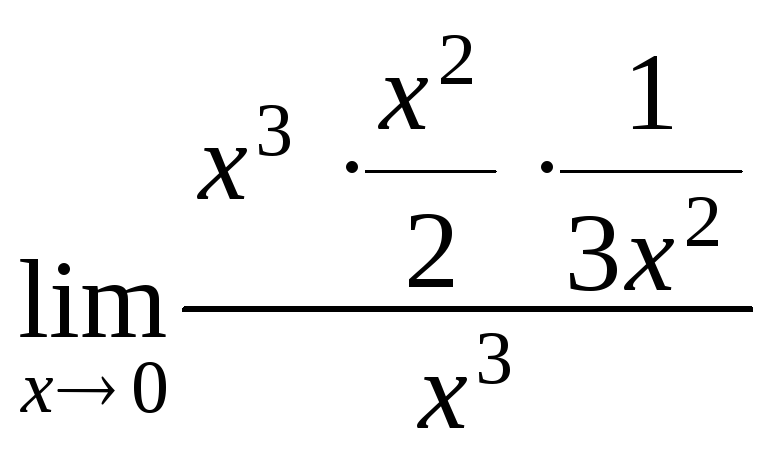 =
=
![]() = 1/6.
= 1/6.
ж)
Подставляем
в функцию предельное значение переменной
х
= 0: за знаком предела
![]() получаем
неопределенность
получаем
неопределенность
![]() .
Для раскрытия неопределенности
воспользуемся эквивалентными малыми.
Поскольку в окрестности точких
= 0: 1 – cos
α(х)
~ 2(х)/2,
то в окрестности этой точке справедливо
приблизительное равенство cos
α(х)
≈ 1 – 2(х)/2,
и, следовательно, cos
2x
– cos
x
≈ (1 – 4x2/2)
– (1 – x2/2)
= 3x2/2;
поскольку arc
tg
α(х)
~ α(х),
то arc
tg2
3х
~ (3х)2
= 9х2;
поскольку sin
α(х)
~ α(х),
то sin2
2х
~ (2х)2
= 4х2.
.
Для раскрытия неопределенности
воспользуемся эквивалентными малыми.
Поскольку в окрестности точких
= 0: 1 – cos
α(х)
~ 2(х)/2,
то в окрестности этой точке справедливо
приблизительное равенство cos
α(х)
≈ 1 – 2(х)/2,
и, следовательно, cos
2x
– cos
x
≈ (1 – 4x2/2)
– (1 – x2/2)
= 3x2/2;
поскольку arc
tg
α(х)
~ α(х),
то arc
tg2
3х
~ (3х)2
= 9х2;
поскольку sin
α(х)
~ α(х),
то sin2
2х
~ (2х)2
= 4х2.
Получаем:
![]() =
=
![]() =
=
![]() = 0,3.
= 0,3.
з)
Подставляем
в функцию предельное значение переменной
х
= 2: за знаком предела
![]() получаем
неопределенность (1∞).
Для раскрытия неопределенности
воспользуемся формулу, получаемую как
следствие 2-го замечательного предела:
получаем
неопределенность (1∞).
Для раскрытия неопределенности
воспользуемся формулу, получаемую как
следствие 2-го замечательного предела:
![]() у(х)
=
у(х)
=
![]() u(x)β(x)
= (1∞)
= exp[
u(x)β(x)
= (1∞)
= exp[![]() (β(x)·(u(x)
– 1))].
Имеем: х0
= 2; u(x)
=
(β(x)·(u(x)
– 1))].
Имеем: х0
= 2; u(x)
=
![]() ;
(x)
=
;
(x)
=
![]() .
Следовательно,
.
Следовательно,![]() = exp[
= exp[![]() (
(![]() (
(![]() – 1))].
– 1))].
Находим
![]() (
(![]() (
(![]() – 1)) =
– 1)) =![]() (
(![]()
![]() )
=
)
=![]()
![]() =
=![]()
![]() =
=![]() 4,5
= 4,5. Т.о.,
4,5
= 4,5. Т.о.,
![]() = e4,5.
= e4,5.
и)
Найти
предел числовой последовательно
![]() ,
используя возможность перехода к
непрерывному аргументу:
,
используя возможность перехода к
непрерывному аргументу:![]() =
=![]() .
Поскольку для предела отношения
многочленов прих
получаем
.
Поскольку для предела отношения
многочленов прих
получаем![]() =
=![]() =1, то для исходного предела имеем
неопределенность (1∞),
поэтому для раскрытия этой неопределенности
воспользуемся формулой, получаемой
как следствие 2-го замечательного
предела:
=1, то для исходного предела имеем
неопределенность (1∞),
поэтому для раскрытия этой неопределенности
воспользуемся формулой, получаемой
как следствие 2-го замечательного
предела:
![]() у(х)
=
у(х)
=
![]() u(x)β(x)
= (1∞)
= exp[
u(x)β(x)
= (1∞)
= exp[![]() (β(x)·(u(x)
– 1))].
Имеем: х0
= + ;
u(x)
=
(β(x)·(u(x)
– 1))].
Имеем: х0
= + ;
u(x)
=
![]() ;(x)
= 3х2
+ 2. Следовательно,
;(x)
= 3х2
+ 2. Следовательно,
![]() = exp[
= exp[![]() ((3х2
+ 2)(
((3х2
+ 2)(![]() – 1))].
– 1))].
Находим
![]() ((3х2
+ 2)(
((3х2
+ 2)(![]() – 1)) =
– 1)) =![]() ((3х2
+ 2)
((3х2
+ 2)![]() )
=
)
=![]()
![]() =
=
![]()
![]() =
=![]() (–21)
= – 21. Следовательно,
(–21)
= – 21. Следовательно,
![]() =
=![]() = е–
21.
= е–
21.
Ответ:
а) 2/9; б)
2; в)
–
3; г)
3/4;
д)
1/(![]() );
е)
1/6; ж)
0,3; з)
e4,5;
и)
е
–
21.
);
е)
1/6; ж)
0,3; з)
e4,5;
и)
е
–
21.
2.
Исследовать
функцию f(x)
на непрерывность, установить тип точек
разрыва и построить график функции в
окрестности точек разрыва:
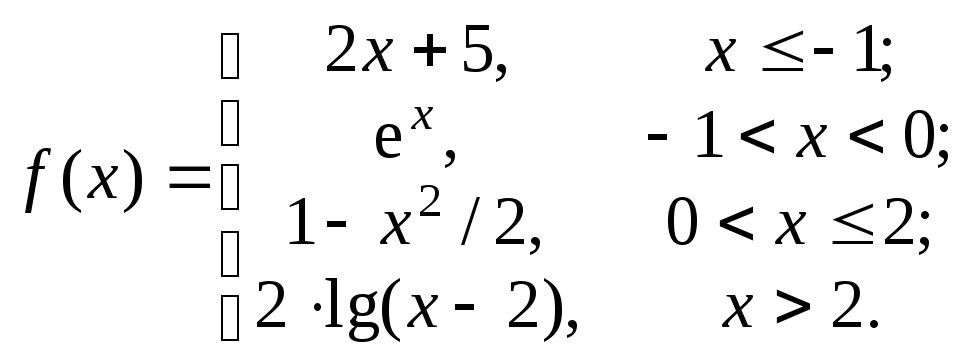
Решение.
Найдем односторонние пределы функции f(x) в граничных точках интервалов ее различного задания:
f(–1
– 0) =
![]() (2х
+5) = 3; f(–1
+ 0) =
(2х
+5) = 3; f(–1
+ 0) =![]() ех
= е
–1
≈ 1/2,7183 ≈ 0,34;
ех
= е
–1
≈ 1/2,7183 ≈ 0,34;
f(–
0) =
![]() ех
= е0
= 1; f(+
0) =
ех
= е0
= 1; f(+
0) =![]() (1
– х2/2)
= 1;
(1
– х2/2)
= 1;
f(2
– 0) =
![]() (1
– х2/2)
= –1; f(2
+ 0) =
(1
– х2/2)
= –1; f(2
+ 0) =
![]() 2lg(x
– 2) = 2
2lg(x
– 2) = 2![]() lg(x
– 2) = – .
lg(x
– 2) = – .
Согласно полученным значениям односторонних пределов функция f(x) имеет: в точке х = –1 разрыв 1-го рода; в точке х = 0 разрыв 1-го рода (причем, поскольку конечный предел слева равен пределу справа, а функция в точке х = 0 не определена, то это, так называемый, устранимый разрыв); в точке х = 2 разрыв 2-го рода.
Для построения графика функции f(x) в окрестностях ее точек разрыва воспользуемся значениями этой функции в некоторых дополнительных точках:
х –2 –3 у –1 –1
х 1 2 у 1/2 –1
у(х) = 2х + 5:
у(х) = (1 – х2/2):
х 2,5 3 4 5 6 у ≈ – 0,6 0 ≈ 0,6 ≈ 1 ≈ 1,2
у(х) = 2lg(x – 2):

Ответ: в точке х = –1 разрыв 1-го рода;
в точке х = 0 разрыв 1-го рода;
в точке х = 2 разрыв 2-го рода.
