Садовский М.В. Квантовая теория поля. Часть 2

30

:

¨á. 2-1

¨á. 2-2

¥«¨ç¨­	N	®á®¡®© ஫¨ ­¥ ¨£à ¥â, íâ® ¯à®áâ® ­®à¬¨à®¢®ç­ë© ¬­®¦¨â¥«ì.
§«®¦¥­¨¥ ãàì¥ ¤«ï F (x) ¨¬¥¥â ¢¨¤:
		F (x) = Z	d4k			e;ikx		(2.21)
			(2 )4		k2 ; m2 + i"

а¨бгвбв¢¨¥ i" ! i0+ ¢ §­ ¬¥­ ⥫¥ ¤¨ªâã¥â ¢ë¡®à ¯ã⨠¨­â¥£à¨à®¢ ­¨ï ¯® k0,
¢ ᮮ⢥âá⢨¨ á 䥩­¬ ­®¢áª¨¬ ¯à ¢¨«®¬ ®¡å®¤ ¯®«îᮢ ¯à¨ k0			=		pk2 + m2.
2			2			2		i", â.¥.
®«îá à ᯮ« £ îâáï ¢ â®çª å, ®¯à¥¤¥«ï¥¬ëå ãà ¢­¥­¨¥¬: k0 = k				+ m			;
¯à¨
k0 = p		i = E i
	k2 + m2							(2.22)
ª ª íâ® ¯®ª § ­® ­ ¨á.2-1. ¯à¥¤¥«¥ ! 0(" ! 0) í⨠¯®«îá			ᤢ¨£ îâáï ­
¤¥©á⢨⥫ì­ãî ®áì ¨ ¯ãâì ¨­â¥£à¨à®¢ ­¨ï ¯à®å®¤¨â ª ª ¯®ª § ­® ­					¨á.2-2.

ëè¥ ¬ë ¢¨¤¥«¨, çâ® â ª®© ¯®¤å®¤ ᮮ⢥âáâ¢ã¥â \¯®¢®à®âã" ¢à¥¬¥­­®© ®á¨ ­ ¬ «ë© 㣮« ¢ ª®¬¯«¥ªá­®© ¯«®áª®á⨠¢à¥¬¥­¨. â® ¯®§¢®«ï¥â ­ ¬ ¯à ¢¨«ì­® ®¡¥á¯¥ç¨âì £à ­¨ç­ë¥ ãá«®¢¨ï ¤«ï ¬¯«¨âã¤ë ¯¥à¥å®¤ ¢ ªã㬠{ ¢ ªãã¬. ® íâ®

¦¥ ¬®¦­® ®¡¥á¯¥ç¨âì, ®áãé¥á⢨¢ â ª®© ¯®¢®à®â ¨ ­	ª®­¥ç­ë© 㣮« à ¢­ë© ; =2,
â ª çâ® t ! ;it(! ;i1). ᫨ ¢¢¥á⨠®¡®§­ 祭¨¥
x4 = it = ix0	(2.23)

â® ¤ ­­ë© ¯à¥¤¥« ᮮ⢥âáâ¢ã¥â x4 ! 1. ª®¥ ¯à®áâà ­á⢮ { ¢à¥¬ï (á ¬­¨¬ë¬ ¢à¥¬¥­¥¬) ï¥âáï ¥¢ª«¨¤®¢ë¬, ¨­¢ ਠ­â­ë© ¨­â¥à¢ « (à ááâ®ï­¨¥ ¬¥¦¤ã ¤¢ã¬ï

; 1 X anx2 !

2 n n

:

31

¡«¨§ª¨¬¨ â®çª ¬¨) ¢ ­¥¬ ¨¬¥¥â ¢¨¤:

						4
ds2 = ;(dx0)2 ; (dx)2 ; (dy)2 ; (dz)2 = ;						=1	(dx )2	(2.24)
						X
¨¬¯ã«ìá­®¬ ¯à®áâà ­á⢥ ¬®¦­®, ᮮ⢥âá⢥­­®, ¢¢¥áâ¨
k4 = ;ik0								(2.25)
â ª çâ®				d4kE = d3kdk4 = ;id4k
k2 = ;(k12 + k22 + k32 + k42) = ;kE2								(2.26)
£¤¥ ¨­¤¥ªá E ®¡®§­ ç ¥â ¥¢ª«¨¤®¢® ¨¬¯ã«ìá­®¥ ¯à®áâà ­á⢮. ਠí⮬ 䥩­¬ -
­®¢áª¨© ¯à®¯ £ â®à ¯à¨­¨¬ ¥â ¢¨¤:
F (x) = ;i	Z	d4kE e;ikx						(2.27)
		(2 )4 k2 + m2
				E

¬¥â¨¬, çâ® íâ® ¢ëà ¦¥­¨¥3 , á â®ç­®áâìî ¤® ;i, ᮢ¯ ¤ ¥â á ª®à५ï樮­­®© ä㭪樥© à­è⥩­ { ¥à­¨ª¥ ⥮ਨ ªà¨â¨ç¥áª¨å ¥­¨© ¢ ç¥âëà¥å¬¥à­®¬ ¯à®áâà ­á⢥ [14, 15, 35], ¥á«¨ áç¨â âì, çâ® m2 T ; Tc , £¤¥ Tc { ⥬¯¥à âãà ä - §®¢®£® ¯¥à¥å®¤ II த (¤«ï ¯à®áâ®âë ¨¬¥¥¬ ¢ ¢¨¤ã ®¡« áâì ⥬¯¥à âãà T > Tc).¤¥áì ¬ë ¢¯¥à¢ë¥ áâ «ª¨¢ ¥¬áï á £«ã¡®ª®© á¢ï§ìî ª¢ ­â®¢®© ⥮ਨ ¯®«ï ¨ ᮢà¥- ¬¥­­®© ⥮ਨ ªà¨â¨ç¥áª¨å ¥­¨© (áâ â¨áâ¨ç¥áª®© 䨧¨ª®©) [14, 15]. § (2.7), á ãç¥â®¬ d4x = ;id4xE ¨ (@ ')2 = ;(@E ')2 ¯®«ãç ¥¬ ¯à®¨§¢®¤ï騩 ä㭪樮­ « ¢ ¥¢ª«¨¤®¢®© ⥮ਨ ¯®«ï ¢ ¢¨¤¥:

	Z D		;Z		2		;
Z0E [J] =		' exp		d4xE	1	[(@E')2 + m2'2]		'J		(2.28)

çâ®, ¯® áã⨠¤¥« , ᮢ¯ ¤ ¥â á® áâ â¨áâ¨ç¥áª®© á㬬®© £ ãáᮢ®© ¬®¤¥«¨ ä §®¢®£® ¯¥à¥å®¤ (â.¥. ⥮ਨ ­¤ ã [35] ¡¥§ ãç¥â ç«¥­®¢ '4 ¨ ¢ëè¥) ¤«ï ᪠«ïà­®£®

¯ à ¬¥âà ¯®à浪 ', ¢§ ¨¬®¤¥©áâ¢ãî饣® á ¢­¥è­¨¬ ¯®«¥¬ J [14, 15].

㭪樮­ «ì­®¥ ¨­â¥£à¨à®¢ ­¨¥.

¥à¥©¤¥¬ ª ®¡á㦤¥­¨î ä㭪樮­ «ì­®£® ¨­â¥£à¨à®¢ ­¨ï á ä®à¬ «ì­®© â®çª¨ §à¥­¨ï. ç­¥¬ á å®à®è® ¨§¢¥áâ­®© ­ ¬ ä®à¬ã«ë ¤«ï ¨­â¥£à « ã áá®­ { ãáá (1.28):

1		1		2		2
Z;1 dxe; 2 ax					= r a			(2.29)
«¥¥ ¯à¥¤¥«ë ¨­â¥£à¨à®¢ ­¨ï ¢á¥£¤	¯®¤à §ã¬¥¢ ¥¬ ®â ;1 ¤® 1 ¨ ­¥ ¢ë¯¨áë-
¢ ¥¬. ®§ì¬¥¬ ¯à®¨§¢¥¤¥­¨¥ n èâ㪠⠪¨å ¨­â¥£à «®¢:

Z dx1dx2:::dxn exp

3 ¤¥áì ­¥â ¯à®¡«¥¬ë ®¡å®¤ ¯®«îᮢ { ®­¨ «¥¦ â ­

(2 )n=2

= n 1=2 (2.30)

Qi=1 ai

¬­¨¬®© ®á¨ ¢ â®çª å k4 = ipkE2 + m2.

32 :

ãáâì A { ¤¨ £®­ «ì­ ï ¬ âà¨æ á í«¥¬¥­â ¬¨ a1; a2; :::; an, x { n-¬¥à­ë© ¢¥ªâ®à (á⮫¡¥æ) á ª®¬¯®­¥­â ¬¨ x1; x2; :::; xn. ®£¤ ¯®ª § ⥫ì íªá¯®­¥­âë ¢ (2.30) ¬®¦­®

§ ¯¨á âì ¢ ¢¨¤¥ ᪠«ïà­®£® ¯à®¨§¢¥¤¥­¨ï:

	(x; Ax) =			a x2			(2.31)
				n	n
			n
			X
¤¥â¥à¬¨­ ­â ¬ âà¨æë A ¥áâì:
					n
DetA = a1a2:::an =						ai	(2.32)
					i=1
					Y
®£¤ (2.30) § ¯¨è¥âáï ª ª:
Z dnxe;	1	(x;Ax) = (2 )n=2(DetA);1=2					(2.33)
	2

®áª®«ìªã íâ® à ¢¥­á⢮ á¯à ¢¥¤«¨¢® ¤«ï «î¡®© ¤¨ £®­ «ì­®© ¬ âà¨æë, ®­® â ª¦¥ á¯à ¢¥¤«¨¢® ¨ ¤«ï «î¡®© ¤¥©á⢨⥫쭮© ᨬ¬¥âà¨ç­®© ¬ âà¨æë, ¯®áª®«ìªã ¢á¥- £¤ áãé¥áâ¢ã¥â «¨­¥©­®¥ ¯à¥®¡à §®¢ ­¨¥, ¯à¨¢®¤ï饥 â ªãî ¬ âà¨æã ª ¤¨ £®­ «ì- ­®¬ã ¢¨¤ã. ¯à¥¤¥«¨¬ ⥯¥àì ¬¥àã ¨­â¥£à¨à®¢ ­¨ï ª ª:

		[dx] = (2 );n=2dnx					(2.34)
®£¤	(2.33) ¯¥à¥¯¨áë¢ ¥âáï ¢ ¢¨¤¥:
		Z [dx]e;	1	(x;Ax) = (DetA);1=2			(2.35)
			2
⮠ᮮ⭮襭¨¥ «¥£ª® ®¡®¡é ¥âáï ­					á«ãç ©, ª®£¤	¢ íªá¯®­¥­â¥ á⮨⠪¢ ¤à â¨ç-
­ ï ä®à¬ ®¡é¥£® ¢¨¤ :
		Q(x) = 1			(x; Ax) + (b; x) + c		(2.36)
		2
®¦­® ¤¥©á⢮¢ âì ª ª ¯à¨ ¢ë¢®¤¥ (1.35). ®à¬						(2.36) ¤®á⨣ ¥â ¬¨­¨¬ã¬ ¯à¨
x = ;A;1b ¨ ¯à¥¤áâ ¢«ï¥âáï ¢ ¢¨¤¥:					1
		Q(x) = Q(x) + 2[x ; x; A(x ; x)]					(2.37)
®£¤	áà §ã ¨¬¥¥¬	­ «®£ (1.35) ¢ ¢¨¤¥:
Z	[dx] exp ; 2	[(x; Ax) + (b; x) + c = exp 2(b; A;1b ; c) (DetA);1=2					(2.38)
	1				1

£¤¥ A;1 ®¡®§­ ç ¥â ®¡à â­ãî ¬ âà¨æã.

áᬮâਬ ⥯¥àì á«ãç © íନ⮢ëå ¬ âà¨æ. ®§¢¥¤¥¬ (2.29) ¢ ª¢ ¤à â ¨ § -

¯¨è¥¬:

2

dxdye;

1

a(x2+y2) =

(2.39)

2

1

;

a

iyZ, â ª çâ® (¢ëç¨á«ïï 类¡¨ ­ ¯¥à¥å®¤

¢¥¤¥¬ z = x + iy ¨ z = x

®â x; y ª z; z )

¨¬¥¥¬ dxdy = ;

idz dz, ¯®á«¥ 祣® (2.39) § ¯¨áë¢ ¥âáï ª ª:

2

Z

dz

dz

1

e;az

z = a

(2.40)

(2 i)1=2

(2 i)1=2

:	33
¡®¡é¨¬ íâã ä®à¬ã«ã, ­ «®£¨ç­® ¯¥à¥å®¤ã ®â (2.30) ª (2.35), ¢¢¥¤ï ¯®«®¦¨â¥«ì­®
®¯à¥¤¥«¥­­ãî íନ⮢㠬 âà¨æã A ¨ ¬¥àã ¨­â¥£à¨à®¢ ­¨ï
[dz] = (2 );n=2dnz	(2.41)
®£¤ ¯®«ã稬:
Z [dz ][dz]e;(z ;Az) = (DetA);1	(2.42)

ᥠ¢ë¯¨á ­­ë¥ ä®à¬ã«ë ¢¯®«­¥ áâண¨¥, ®­¨ ¯à¥¤áâ ¢«ïîâ ᮡ®© ¯àאַ¥ ®¡®¡é¥- ­¨¥ \®¤­®¬¥à­ëå" ¨­â¥£à «®¢ ­ á«ãç © ª®­¥ç­®¬¥à­®£® ¢¥ªâ®à­®£® ¯à®áâà ­á⢠.஢¥¤¥¬ ⥯¥àì ä®à¬ «ì­®¥ ®¡®¡é¥­¨¥ ­ á«ãç © ¡¥áª®­¥ç­®¬¥à­®£® ä㭪樮- ­ «ì­®£® ¯à®áâà ­á⢠. ãáâì à¥çì ¨¤¥â ® ¯à®áâà ­á⢥ ¤¥©á⢨⥫ì­ëå ä㭪権 '(x ). ®¦­® ®¯à¥¤¥«¨âì ¨å ᪠«ïà­®¥ ¯à®¨§¢¥¤¥­¨¥:

	('; ') = Z d4x['(x)]2	(2.43)
¡®¡é¥­¨¥ ¢ëà ¦¥­¨ï (2.35) ¥áâì:
Z	1
	D'(x) exp ; 2 Z dx'(x)A'(x) = (DetA);1=2	(2.44)
£¤¥ A { ­¥ª®â®àë© ®¯¥à â®à, ¤¥©áâ¢ãî騩 ­ ä㭪樨 '(x):
	A'(x) = Z dyA(x; y)'(y)	(2.45)

¥£® ¤¥â¥à¬¨­ ­â ®¯à¥¤¥«ï¥âáï, ¥áâ¥á⢥­­®, ª ª ᮮ⢥âáâ¢ãî饥 ¯à®¨§¢¥¤¥­¨¥ ᮡá⢥­­ëå §­ 祭¨©. ¥à ¨­â¥£à¨à®¢ ­¨ï D'(x) = [d'(x)]. ᥠíâ® á«¥¤ã¥â ¯®- ­¨¬ âì, ª ª ®¡ëç­®, ¢ ¢¨¤¥ ¯à¥¤¥«ì­®£® ¢ëà ¦¥­¨ï ⨯ (2.5). ëà ¦¥­¨¥ (2.44) ®¡ëç­® ­ §ë¢ îâ £ ãáá®¢ë¬ ä㭪樮­ «ì­ë¬ ¨­â¥£à «®¬.

᫨ '(x) ¯à¥¤áâ ¢«ï¥â ᮡ®© ª®¬¯«¥ªá­ãî äã­ªæ¨î (¯®«¥), â® ¢®§­¨ª ¥â ¥áâ¥- á⢥­­®¥ ®¡®¡é¥­¨¥ (2.42):

	1	Z dx' (x)A'(x) = (DetA);1
	Z D' (x)D'(x) exp ; 2
£¤¥ A { íନ⮢ ®¯¥à â®à.
¡®¡é¥­¨¥ (2.38) ¤«ï á«ãç ï ¢¥é¥á⢥­­ëå ¯®«¥© '(x) ¨¬¥¥â ¢¨¤:
Z	D'(x) exp ; 2 Z dx Z dy'(x)A(x; y)'(y) + Z dxB(x)'(x) + c =
	1

= exp 12 Z dx Z dyB(x)A;1(x; y)B(y) ; c (DetA);1=2

(2.46)

(2.47)

£¤¥ A;1 (x; y) ®¡®§­ ç ¥â ᮮ⢥âáâ¢ãî騩 ®¡à â­ë© ®¯¥à â®à. «ï ª®¬¯«¥ªá­ëå

¯®«¥© ¢®§­¨ª ¥â ᮢ¥à襭­® ­ «®£¨ç­®¥ ¢ëà ¦¥­¨¥, ®â«¨ç î饥áï ®â (2.47) ­ - «¨ç¨¥¬ ¨­â¥£à¨à®¢ ­¨ï ¯® ' ¨ ', â ª¦¥ § ¬¥­®© (DetA);1=2 ­ (DetA);1 .

¥à­¥¬áï ⥯¥àì ª à áᬮâ७¨î ®¡é¥£® ¢ëà ¦¥­¨ï ¤«ï ¯à®¨§¢®¤ï饣® äã­ª- 樮­ « ¯®«ï «¥©­ { ®à¤®­ (2.10):

Z0 [J] = Z D' exp ;i Z	d4x 2	'(2	+ m2	; i")' ; 'J	(2.48)
	1

34	:
	â®ï騩 §¤¥áì ä㭪樮­ «ì­ë© ¨­â¥£à « ¨¬¥¥â, ª ª à §, £ ãáᮢ ¢¨¤ (2.47), ¯à¨ç¥¬
	A(x; y) = i(2 + m2 ; i") (x ; y), B(x) = ;iJ(x), c = 0. ®£¤ ¨§ (2.47) ¯®«ãç ¥¬:
				i
	Z0[J] = exp				Z dxdyJ(x)(2 + m2 ; i");1J(y) [iDet(2 + m2 ; i")];1=2					(2.49)
				2
	®§­¨ªè¨© §¤¥áì ¤¥â¥à¬¨­ ­â ¬®¦­® ¯¥à¥¯¨á âì, á ¯®¬®éìî (2.44), ª ª:
	[iDet(2 + m2 ; i")];1=2 = Z D'(x) exp ;					i		+ m2 ; i")'(x)
							Z dx'(x)(2			(2.50)
						2
	®¡à â­ë© ®¯¥à â®à:
					(2 + m2 ; i");1 = ; F (x ; y)					(2.51)
	çâ® á«¥¤ã¥â ­¥¯®á।á⢥­­® ¨§ (2.17). ®£¤ ¢ëà ¦¥­¨¥ (2.49) ᢮¤¨âáï ª:
		i						i
	Z0[J] = exp ;		Z dxdyJ(x) F (x ; y)J(y) Z D' exp ;						Z dx'(2 + m2 ; i")'
		2						2
										(2.52)

ç⮠ᮢ¯ ¤ ¥â á (2.19). ª¨¬ ®¡à §®¬, ¯àאַ¥ ¢ëç¨á«¥­¨¥ ¯® ¯à ¢¨« ¬ ä㭪樮-

­«ì­®£® ¨­â¥£à¨à®¢ ­¨ï ¤ ¥â ¨§¢¥áâ­ë© ­ ¬ ®â¢¥â ¤«ï ¯à®¨§¢®¤ï饣® ä㭪樮-

­« , ¯®«ã祭­ë© ¢ëè¥ ­¥áª®«ìª® \®¡å®¤­ë¬" ¯ã⥬.

®«ã祭­ë¥ ¢ëè¥ ä®à¬ã«ë ¤«ï £ ãáᮢëå ä㭪樮­ «ì­ëå ¨­â¥£à «®¢ ¡ã¤ãâ è¨à®ª® ¨á¯®«ì§®¢ âìáï ­¨¦¥.

㭪樨 ਭ ᢮¡®¤­ëå ç áâ¨æ.

®ª ¦¥¬ ⥯¥àì, çâ® Z0[J] ï¥âáï ¯à®¨§¢®¤ï騬 ä㭪樮­ «®¬ ¤«ï ä㭪権ਭ ᢮¡®¤­ëå ç áâ¨æ. «ï í⮣® à §«®¦¨¬ (2.20) ¢ àï¤:

Z0[J ] = N 1 ;

i

Z dxdyJ(x) F (x ; y)J (y)+

2

1

i 2

2

+

Z

dxdyJ (x) F (x ; y)J(y)

+

2!

2

1

i

3

3

+

Z

dxdyJ (x) F (x ; y)J(y)

+ :::)

3!

2

¢®¤ï äãàì¥ - ¯à¥¤áâ ¢«¥­¨¥ ¨áâ®ç­¨ª :

J(x) = Z d4pJ (p)e;ipx

¨ ¨á¯®«ì§ãï (2.21) «¥£ª® ¯®«ãç ¥¬:

i

d4xd4yJ (x) F (x

y)J(y) =

i

(2 )4

d4k

J (;k)J(k)

; 2 Z

;

;2

Z

k2 ; m2 + i"

(2.53)

(2.54)

(2.55)

Z[J ] =< 0; 1j0; ;1 >J

:

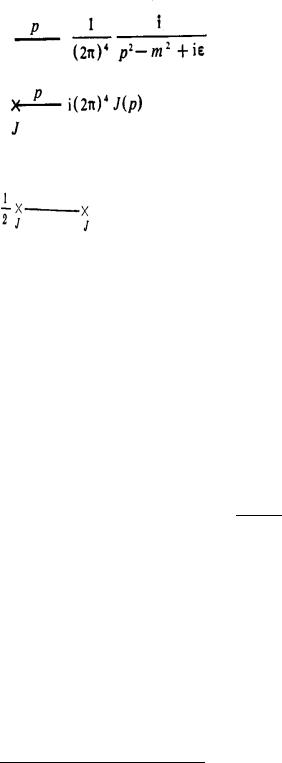
35

¨á. 2-3

¨á. 2-4

®¯®áâ ¢¨¬ ­ «¨â¨ç¥áª¨¬ ¢ëà ¦¥­¨ï¬ £à ä¨ç¥áª¨¥ í«¥¬¥­âë, ª ª íâ® ¯®ª § ­®

­	¨á.2-3. ®£¤ ¢ëà ¦¥­¨î (2.55) ᮮ⢥âáâ¢ã¥â ¤¨ £à ¬¬ , ¯®ª § ­­ ï ­ ¨á.2-
4.	१ã«ìâ â¥, à §«®¦¥­¨¥ ¯à®¨§¢®¤ï饣® ä㭪樮­ « ( ¬¯«¨âã¤ë ¯¥à¥å®¤

¢ ªã㬠{ ¢ ªãã¬) (2.53) ¯à¥¤áâ ¢«ï¥âáï ¤¨ £à ¬¬ ¬¨, ¯®ª § ­­ë¬¨ ­ ¨á.2-54.¨¤¨¬, çâ® íâ®â àï¤ ®¯¨áë¢ ¥â à á¯à®áâà ­¥­¨¥ 1, 2, 3 ¨ â. ¤. \ç áâ¨æ" ¬¥¦¤ã ¨á- â®ç­¨ª ¬¨, â ª çâ® ¬ë ¨¬¥¥¬ ¤¥«® á ¬­®£®ç áâ¨ç­®© ⥮ਥ©. ¦¥ ®âáî¤ ­¥âà㤭® ¯®­ïâì, çâ® Z0 [J] ï¥âáï ¯à®¨§¢®¤ï騬 ä㭪樮­ «®¬ ¤«ï ä㭪権 ਭ à á-

ᬠâਢ ¥¬®© ⥮ਨ ¯®«ï.

®ïá­¨¬ ä®à¬ «ì­ãî áâ®à®­ã ¤¥« . áᬮâਬ, ­ ¯à¨¬¥à, à §«®¦¥­¨¥ ¢ àï¤ ­¥ª®â®à®© ä㭪樨 F (y1; :::; yk) ®â k ¯¥à¥¬¥­­ëå y1; :::; yk:

1

k

k

1

F fyg F (y1; :::; yk) =

:::

Tn(i1; :::; in)yi1:::yin

(2.56)

n=0 i1=0

in=0

n!

£¤¥

X X X

@nF fyg

Tn =

y=0

(2.57)

@y1:::@yn j

¥à¥©¤¥¬ ⥯¥àì ª ¨­âã¨â¨¢­®¬ã ¯à¥¤¥«ã, ª®£¤

¯¥à¥¬¥­­ë¥ ®¡à §ãîâ ª®­â¨­ãã¬: i ! x; yi(i =

1; :::; k) ! y(x);

i ! dx ¨ ¯®«ã稬 á⥯¥­­®¥ à §«®¦¥­¨¥ ¤«ï ä㭪樮­ « :

P

R F [y] =

1

1

dx1:::dxn

Tn(x1; :::; xn)y(x1):::y(xn)

(2.58)

n=0

n!

£¤¥

XZ

Tn(x1; :::; xn) =

:::

F [y]jy=0

(2.59)

y(x1)

y(xn)

í⮬ á«ãç ¥ ® ¢¥«¨ç¨­¥ F [y]

¨ £®¢®àïâ ª ª ® ¯à®¨§¢®¤ï饬 ä㭪樮­ «¥ ¤«ï ä㭪権

Tn(x1; :::xn).

и ¯а®¨§¢®¤пй¨© дг­ªж¨®­ « Z[J ] ­ ¤® ¥й¥ ®в­®а¬¨а®¢ вм. ­, ª ª ¬л ¢¨- ¤¥«¨, ¯а®¯®аж¨®­ «¥­ ¬¯«¨вг¤¥ ¯¥а¥е®¤ ¢ ªгг¬ - ¢ ªгг¬ ¢ ¯а¨бгвбв¢¨¨ ¨бв®з- ­¨ª J. бв¥бв¢¥­­®© ­®а¬¨а®¢ª®© п¢«п¥вбп гб«®¢¨¥ Z[J = 0] = 1. ®£¤ ¬®¦¥¬ ­ ¯¨б вм а ¢¥­бв¢®:

(2.60)

4 ®à¬¨à®¢®ç­ë© ¬­®¦¨â¥«ì N §¤¥áì ®¯ã饭.

36

:

¨á. 2-5

â ª çâ® ãá«®¢¨¥ Z[0] = 1 ¢ë¯®«­ï¥âáï

¢â®¬ â¨ç¥áª¨. ®í⮬ã (2.10) ¨ (2.20) á«¥-

¤ã¥â ¯¥à¥¯¨á âì ª ª:

' exp

i

d4x

1

'(2 + m2

i")'

'J

2

Z0 [J] =

D

;

1

;

;

(2.61)

R

R D

' exp

R

i

R

d4x

2

'(2 + m2

i")'

i

;

;

Z0[J ] = exp ;

Z

dxdyJ(x) F (x ; y)J (y)

(2.62)

2

⨠­®¢ë¥ ®¯à¥¤¥«¥­¨ï, ®ç¥¢¨¤­®, 㤮¢«¥â¢®àïîâ ãá«®¢¨î Z[J = 0] = 1, çâ® ¨

®¯à ¢¤ë¢ ¥â ®â¡à áë¢ ­¨¥ ­¥áãé¥á⢥­­®£® ­®à¬¨à®¢®ç­®£® ¬­®¦¨â¥«ï N .

㭪樮­ « Z0 [J], ®¯à¥¤¥«ï¥¬ë© ¢ëà ¦¥­¨¥¬ (2.62), ¢ ᮮ⢥âá⢨¨ á (2.59),

ï¥âáï ¯à®¨§¢®¤ï騬 ä㭪樮­ «®¬ ¤«ï ä㭪権:

(x1; :::; xn) =

1

nZ0[J]

jJ=0

(2.63)

in

J (x1)::: J (xn)

ᯮ¬¨­ ï (1.109), ¯®­¨¬ ¥¬, çâ®:

nZ0[J]

jJ=0

= i

n

< 0jT '(x1):::'(xn)j0 >

(2.64)

J(x1)::: J (xn)

â ª çâ®

(x1; :::; xn) =< 0jT '(x1):::'(xn)j0 >

(2.65)

¯à¥¤áâ ¢«ï¥â ᮡ®© ¢ ªã㬭®¥ á।­¥¥ ®â åà®­®«®£¨ç¥áª®£® ¯à®¨§¢¥¤¥­¨ï ¯®«¥- ¢ëå ®¯¥à â®à®¢, â.¥. ï¥âáï n-â®ç¥ç­®© (¯® ç¨á«ã ª®®à¤¨­ â) ä㭪樥© ਭ ¤«ï à áᬠâਢ ¥¬®© ⥮ਨ. â® ®¯à¥¤¥«¥­¨¥ ᮢ¯ ¤ ¥â á à áᬮâ७­ë¬ ¢ëè¥ ®¯à¥¤¥«¥­¨¥¬ ä㭪権 ਭ ¢ ®¯¥à â®à­®¬ ä®à¬ «¨§¬¥ ª¢ ­â®¢®© ⥮ਨ ¯®«ï.ந§¢®¤ï騩 ä㭪樮­ « ¬®¦­® ⥯¥àì § ¯¨á âì ¢ ¢¨¤¥:

	1	in		Z
Z0[J] =	X				dx1:::dxnJ (x1):::J (xn) (x1	; :::; xn)	(2.66)
	n=0 n!

:

37

çâ® ¨ ®§­ ç ¥â, çâ® Z0 [J] ï¥âáï ¯à®¨§¢®¤ï騬 ä㭪樮­ «®¬ ¤«ï ä㭪権ਭ (x1; :::; xn). ¬¥­­® íâ® à §«®¦¥­¨¥ ¨ ¯®ª § ­® £à ä¨ç¥áª¨ ­ ¨á.2-5.

©¬¥¬áï ¢ëç¨á«¥­¨¥¬ ­¥ª®â®àëå ¯à®á⥩è¨å n-â®ç¥ç­ëå ä㭪権 ਭ . - ¯®¬­¨¬, çâ® ¬ë ¨¬¥¥¬ ¤¥«® ᮠ᢮¡®¤­®© ⥮ਥ© ᪠«ïà­®£® ¯®«ï. ç­¥¬ á 2-

â®ç¥ç­®© ä㭪樨:	2Z0[J ]
(x; y) = ;	J (x) J(y)	jJ=0	(2.67)

ëç¨á«¥­¨ï ¬®¦­® ¯à®¢¥á⨠­¥¯®á।á⢥­­®, ¨á¯®«ì§ãï ¯à¨¢¥¤¥­­®¥ ¢ëè¥ ®¯à¥- ¤¥«¥­¨¥ ä㭪樮­ «ì­®© ¯à®¨§¢®¤­®©. ¬¥¥¬:

1 Z0[J]

1

exp ;

i

dx1dx2J(x1) F (x1 ; x2)J (x2) =

=

i

Z

i J (x)

J(x)

2

= ;Z dx1 F (x ; x1)J (x1 ) exp ;

i

Z dx1dx2J (x1) F (x1 ; x2)J (x2)

(2.68)

2

1

1

i

i

i

Z0

[J] = i F (x ; y) exp ;

Z J F J +

J(x)

J (y)

2

+Z dx1 F (x ; x1)J(x1) Z dx1 F (y ; x1) exp ;

i

Z J F J

(2.69)

2

£¤¥ ¨á¯®«ì§ã¥¬ ᮪à 饭­ãî § ¯¨áì íªá¯®­¥­âë. ®« £ ï ⥯¥àì J = 0, ¯®«ãç ¥¬:

1

1

Z0

[J]jJ=0 = i F (x ; y)

(2.70)

i

i

J(x)

J(y)

¨«¨

(x; y) = i F (x ; y)

(2.71)

á­®, çâ® 2-â®ç¥ç­ ï äã­ªæ¨ï ਭ , ä ªâ¨ç¥áª¨, ᮢ¯ ¤ ¥â á 䥩­¬ ­®¢áª¨¬ ¯à®- ¯ £ â®à®¬ ᪠«ïà­®© ç áâ¨æë (®¤­®ç áâ¨ç­ ï äã­ªæ¨ï ਭ ᢮¡®¤­®© ᪠«ïà- ­®© ç áâ¨æë). ® à áᬮâਬ ¥é¥ à § ¥¥ 䨧¨ç¥áª¨© á¬ëá«. ஢¥¤¥¬ á­ ç « ¢ëç¨á«¥­¨ï ¢ ®¯¥à â®à®­®¬ ¯®¤å®¤¥. ® ®¯à¥¤¥«¥­¨î åà®­®«®£¨ç¥áª®£® ¯à®¨§¢¥- ¤¥­¨ï ¨¬¥¥¬:

(x; y) =< 0jT '(x)'(y)j0 >=
=< 0j (x0 ; y0 )'(x)'(y) + (y0 ; x0 )'(y)'(x)j0 >	(2.72)
¥à¢®¥ á« £ ¥¬®¥ §¤¥áì ¯à¥¤áâ ¢«ï¥â ᮡ®© ¬¯«¨âã¤ã ¢¥à®ïâ­®á⨠஦¤¥­¨ï ç -

áâ¨æë ¢ â®çª¥ y ¢ ¬®¬¥­â ¢à¥¬¥­¨ y0 ¨ ¥¥ ¯®á«¥¤ãî饣® ã­¨ç⮦¥­¨ï ¢ â®çª¥ x ¢ ¬®¬¥­â x0 . â®à®¥ á« £ ¥¬®¥ ¤ ¥â ¬¯«¨âã¤ã ¢¥à®ïâ­®á⨠஦¤¥­¨ï ç áâ¨æë ¢ â®çª¥ x ¢ ¬®¬¥­â x0 ¨ ¥¥ ã­¨ç⮦¥­¨ï ¢ â®çª¥ y ¢ ¬®¬¥­â ¢à¥¬¥­¨ y0 . ⨠¯à®æ¥ááë £à ä¨ç¥áª¨ ¯à®¨««îáâà¨à®¢ ­ë ­ ¨á.2-6. 㬬 íâ¨å ¬¯«¨â㤠¨ ¤ ¥â 䥩­¬ - ­®¢áª¨© ¯à®¯ £ â®à. ë §­ ¥¬, çâ® ¢ ®¯¥à â®à­®¬ ¯®¤å®¤¥ ¯®«¥ ' ¬®¦­® § ¯¨á âì ¢ ¢¨¤¥ á㬬ë ç«¥­®¢ á ¯®«®¦¨â¥«ì­ë¬¨ ¨ ®âà¨æ ⥫ì­ë¬¨ ç áâ®â ¬¨ (á¬. « ¢ã

3 ç á⨠I):
'(x) = '(+)(x) + '(;)(x)							(2.73)
£¤¥	d3k
'(+)(x) = Z				1		ake;ikx	(2.74)
	(2 )3
			p	2!k

38

:

¨á. 2-6

(

)

Z

d3k

1

+ ikx

'

;

(x) =

(2 )3

ake

(2.75)

2!k

= p

,

a+

{ ᮮ⢥âáâ¢ãîé¨p

£¤¥ !

k

k2 + m2

; a

¥ ®¯¥à â®àë ஦¤¥­¨ï ¨ ã­¨çâ®-

k

k

¦¥­¨ï. ãç¥â®¬ á¬ëá«

íâ¨å ®¯¥à â®à®¢, ¢ ¢ ªã㬭®¬ á।­¥¬ (2.72) ®áâ îâáï

⮫쪮 ç«¥­ë ¢¨¤ '(+)'(;):

(x; y) = (x0 ;y0) < 0j'(+) (x)'(;) (y)j0 > + (y0 ;x0) < 0j'(+)(y)'(;) (x)j0 > (2.76)

®¤áâ ¢«ïï áî¤ (2.74) ¨ (2.75) ¯®«ãç ¥¬:

(x; y) = Z

d3kd3k0

; y0 )e;

i(kx

;

k0y0)

+ (y0 ; x0)e;

i(ky

;

k0x)

+

(2 )6!k!k0

[ (x0

] < 0jakak0 j0 >

(2.77)

â ª çâ®, ¯¥à¥áâ ¢«ïï ®¯¥à â®àë ¢ ¢ ªã㬭®¬ á।­¥¬ á ¯®¬®éìî ª®¬¬ãâ 樮­­ëå ᮮ⭮襭¨© (â ª, çâ®¡ë ¢ë¤¥«¨âì ®¡à é î騩áï ¢ ­ã«ì ¢ª« ¤ ®â ¨å ­®à¬ «ì­®£® ¯à®¨§¢¥¤¥­¨ï ¨ ­¥­ã«¥¢®© ¢ª« ¤ ®â -ä㭪樨), ¯®«ãç ¥¬:

(x; y) = Z	d3k	[ (x0	; y0 )e;ik(x;y) + (y0	; x0)eik(x;y) ]	(2.78)
	(2 )3!k

¡¥¤¨¬áï, çâ® íâ® ¢ëà ¦¥­¨¥ ¯à®á⮠ᮢ¯ ¤ ¥â á i F (x;y), £¤¥ F (x;y) § ¤ ¥âáï (2.21). ëà ¦¥­¨¥ (2.21) ¬®¦­® ¯¥à¥¯¨á âì ª ª:

d4k

e;ikx

d3kdk0

e;ikx

F (x) = Z

= Z

=

(2 )4

k2 ; m2 + i"

(2 )4 k02

; (k2 + m2) + i"

= Z

d3kdk0 e;ikx

1

1

(2 )4 2!k

;

(2.79)

k0 ; !k + i

k0 + !k ; i

­â¥£à « ¯® k0 âãâ, ª ª ¢á¥£¤ , ¬®¦­® «¥£ª® ¢ëç¨á«¨âì ª®­âãà­ë¬ ¨­â¥£à¨à®¢ - ­¨¥¬. ¯®ª § ⥫¥ íªá¯®­¥­âë á⮨â e;ik0x0 , â ª çâ® ¯à¨ x0 > 0 § ¬ëª ¥¬ ª®­âãà

¨­â¥£à¨à®¢ ­¨ï ¢ ­¨¦­¥© ¯®«ã¯«®áª®á⨠k0, ¨ ¨­â¥£à « ®¯à¥¤¥«ï¥âáï ¢ª« ¤®¬ ®â

¯®«îá ¯à¨ k0 = !k ;i . ਠx0 < 0 § ¬ª­¥¬ ª®­âãà ¨­â¥£à¨à®¢ ­¨ï ¢ ¢¥àå­¥© ¯®- 㯫®áª®á⨠¨ ¢á¥ ®¯à¥¤¥«¨âáï ¢ª« ¤®¬ ¯®«îá ¯à¨ k0 = ;!k +i . ®£¤ , ¯® ⥮६¥

®è¨, ¨¬¥¥¬:

F (x) = Z	d2k eikx
	(2 )3 2!k [ (x0)(;i)e;i!kx0 ; (;x0 )iei!kx0 ]	(2.80)

:				39
®á«¥ § ¬¥­ë ¢® ¢â®à®¬ ¨­â¥£à «¥ k			! ;k ¨ ¯¥à¥®¡®§­ 祭¨ï x ! x;y, ¯®«ãç ¥¬:
F (x ; y) = ;i Z	d3k		; y0)e;ik(x;y) + (y0 ; x0)eik(x;y)]
		[ (x0		(2.81)
	(2 )3!k

ç⮠ᮢ¯ ¤ ¥â á ;i (x; y) ¨§ (2.78). ª¨¬ ®¡à §®¬, 2-â®ç¥ç­ ï äã­ªæ¨ï ਭ , ¢®§­¨ªè ï ¢ ä㭪樮­ «ì­®¬ ¯®¤å®¤¥, ¤¥©á⢨⥫쭮, ᮢ¯ ¤ ¥â á ®¤­®ç áâ¨ç­ë¬ ¯à®¯ £ â®à®¬ ®¯¥à â®à­®© ä®à¬ã«¨à®¢ª¨ ⥮ਨ ¯®«ï.

® çâ® ¯à¥¤áâ ¢«ï¥â ᮡ®© 1-â®ç¥ç­ ï äã­ªæ¨ï? 祢¨¤­®, çâ® ¨§ (2.68) ¨¬¥¥¬:

(x) =< 0jT '(x)j0 >=< 0j'(x)j0 >= 1 Z0 [J]jJ=0 = i J(x)

= ;Z dx1 F (x ; x1)J(x1) exp ; i Z dx1dx2J (x1) F (x1 ; x2)J(x2) jJ=0 = 0 2

(2.82)

{¢ ªã㬭®¥ á।­¥¥ á ¬®£® ¯®«ï à ¢­® ­ã«î!

©¤¥¬ ⥯¥àì 3-â®ç¥ç­ãî äã­ªæ¨î. ¨ää¥à¥­æ¨àãï ¥é¥ à § (2.69), ¯®«ã稬:

	1		1 1							Z0[J] =
	i			i		i
		J(x1)			J(x2)		J(x3)
= ;i F (x2	; x3) Z dx F (x1		; x)J(x)exp ;				i		Z J F J ;
							2
;i F (x2	; x1) Z dx F (x3		; x)J(x)exp ;				i		Z J F J ;
							2
;i F (x3	; x1) Z dx F (x2		; x)J(x)exp ;				i		Z J F J ;
							2

;Z dx F (x2 ; x)J(x)Z dx F (x3 ; x)J(x)Z	dx F (x1 ; x)J (x)exp ;	i		Z	J F J
		2
					(2.83)

çâ® ¯à¨ J = 0, á ®ç¥¢¨¤­®áâìî, ¤ ¥â ­ã«ì. ª¨¬ ®¡à §®¬:

(x1; x2; x3) =< 0jT '(x1)'(x2)'(x3)j0 >= 0

­ «®£¨ç­ë¥ ¢ëç¨á«¥­¨ï ¤ îâ:
		1			1
					::: i				Z0[J ] =
		i J(x1)				J(x4)
= ; F (x2	; x3 ) F (x1	; x4)exp ;				i		Z J F J ;
						2
; F (x2	; x1 ) F (x3	; x4)exp ;				i		Z J F J ;
						2

; F (x3 ; x1) F (x2 ; x4)exp ;	i		Z J F J + :::
	2

£¤¥ ¬­®£®â®ç¨¥¬ ®¡®§­ 祭ë ç«¥­ë, ®¡à é î騥áï ¢ ­ã«ì ¯à¨ J á⢥­­®, ¯®«ãç ¥¬:

(x1; x2; x3; x4) = F (x2 ; x3) F (x1 ; x4 ) + + F (x2 ; x1) F (x3 ; x4) + F (x3 ; x1 ) F (x2 ; x4)

(2.84)

(2.85) = 0. ®®â¢¥â-

(2.86)