Кулик Введение в теорию квантовых вычислений Книга 2 2008

		3		1	2		1	=1, т.е. λ = 1.
	=		–			+
		4		2			2

Тогда

ˆ

ˆ

ˆ

1

0 1

S+

+ S−

S

x

=

=

σ

x

,

σ

x

=

,

2

2

1

0

ˆ

ˆ

ˆ

1

0 −i

S+

− S−

Sy =

=

σ y

, σ y =

0

.

2i

2

i

ˆ

2. Вычислить среднее значение оператора спина S в состоянии

(2.30).

Решение

ˆ

=

1

{σ x ,

σ y , σ z } пред-

Среднее значение оператора спина S

2

ставляет собой вектор

ˆ

1

{ σx

, σ y , σz },

S =

2

компоненты

которого

получаются

усреднением

матриц Паули

(2.41) по состоянию (2.30).

Вычислим

<σx > :

θ

i α

iα

θ

e

cos

0

1

e

cos

2

σ

2

x

=

=

i β

θ

1 0

iβ

θ

e

sin

e

sin

2

2

101

(ei(β−α)

=

−i α

cos(

θ

iβ

sin

θ

e

2

)

e

2

=

=

−i β

sin(

θ

iα

cos

θ

e

2

)

e

2

+ e−i(β−α) )

sin

θ

cos θ

= sin θ cos(β−α) .

2

2

Аналогично, имеем

i α

θ

iα

θ

e

cos

0 −i

e

cos

2

2

σ y =

i β

θ i

0

iβ

θ

=

e

sin

e

sin

2

2

= −i

(ei (β−α)

−e−i (β−α) )

sin

θ

cos θ

=

= sin θ sin(β−α)

,

2

2

i α

θ

iα

θ

e

cos

1

0

e

cos

2

σz

2

=

i β

θ

0

−1

iβ

θ

= cosθ.

e

sin

e

sin

2

2

ˆ

Таким образом, компоненты вектора S имеют вид

ˆ

1

S

=

{ sin θ cos(β−α) , sin θ sin(β−α) , cosθ}.

2

102

	Длина этого вектора равна	1	, а направление задается углами
		2
	θ, β−α, как показано на рис. 2.3.

	iα	cos	θ
e			2
3. Доказать, что спинор				описывает собственное со-
			θ
	iβ	cos
e
			2

стояние	оператора				sˆn = sn		проекции			спина 1 2	на ось
n = sin θcos		(	β−α	)	, sin θsin	(	β−α	)	, cosθ ,	отвечающее	собст-
{									}

венному значению 12 . Сравнить вектор n с направлением векто-

ˆ из предыдущей задачи. Какой вид имеет спинор, отвечаюра S

щий собственному значению проекции на ось n , равному −12 ?

4. Доказать, что любую матрицу М ( 2×2 ) можно представить в виде

М=a0 + a1 σ x +a2 σ y +a3 σ z ,

где σi — матрицы Паули.

Доказательство

u	w	– некоторая произвольная матрица	2×2 .
Пусть М=
v	z

Тогда неизвестные коэффициенты аi (i=0, 1, 2, 3) находятся из условия, что

u w		= a0	1		0		+ a1	0		1		+ a2	0 −i			+ a3	1		0	=
				0	1				1	0				0				0
v	z												i						−1
										103

	a	+ a	a −i a			,
=	0	3	1	2
a1 +i a2			a0 −a3

т.е.

a0 + a3 = ua0 − a3 = z

a1 −i a2 = wa1 +i a2 = v .

Отсюда получаем

a0=	u + z	, a3=	u − z	, a1=	w + v	, a3= i	w − v	.
2		2		2		2

Соотношение (2.44) показывает, что произведение двух (и более) матриц Паули редуцируется к единичной матрице и первым степе-

ням матриц Паули, как и должно быть, так как {1, σi } образуют

полный набор матриц 2×2 . Если в (2.44) сделать замену i ↔ k , а потом вычесть из исходного выражения, то получится коммутаци-

	онное соотношение [σi σk	] = 2 i εikl σl , которое эквивалентно
	ˆ	1
	(2.28), если учесть, что S j =		σ j .
		2

5. Доказать соотношение ( a σ ) (b σ ) = ( a b )+ i [a ×b]σ .

Указание

Воспользоваться свойством (2.44).

6. Пусть {n} есть полный ортонормированный базис гильбертова

пространства состояний квантовой системы, а Fmn =	m		ˆ		n –
			F

матричные элементы линейного оператора ˆ .

F

104

Покажите, что оператор ˆ можно представить в виде

F

ˆ

∑Fmn

m n

.

F =

mn

В

частности,

в двумерном

пространстве состояний с

базисом

{

0 ,

1

} произвольный линейный оператор записывается в виде

ˆ

0 0

+ F01

0 1

+ F10

1 0

+ F11

1 1

.

F = F00

Убедитесь,

что

матрицы

операторов

0 1

+

1 0

,

−i (

0

1

−

1

0

) и

0 0

−

1 1

,

которые написаны

справа в

формулах (2.47), совпадают с матрицами Паули, соответственно, σx , σy и σz . Какой вид имеют матрицы операторов (σ x ±

iσ y )/2?

									ˆ
7. Доказать следующие свойства унитарного оператора U .
							ˆ
(а) Собственные значения U по модулю равны 1.
(б)		ˆ			ˆ				ˆ
		DetU		=1, где DetU		– определитель матрицы U .
			ˆ		ˆ
(в) Если U (λ)= exp(iλF ), где λ – действительный
				ˆ	ˆ	+			ˆ
		параметр, то F = F					. Эрмитовый оператор F
		называется генератором непрерывного унитарного
				ˆ	(λ).
		преобразования U
		ˆ				ˆ		ˆ	обозначает
(г) DetU				(λ)= exp(iλSpF ), где				SpF
				ˆ
		след оператора F .
		ˆ		ˆ		ˆ	(λ2 ).	Это	соотношение
(д) U (λ1			+ λ2 ) = U (λ1 )U

называется групповым свойством.

(г) Произведение унитарных операторов является унитарным оператором.

105

Доказательство

ˆ				ˆ	являются унитарными, т.е. удовлетво-
Пусть операторы U1			и U 2
ряют условиям
ˆ ˆ	+		ˆ	+	ˆ	ˆ	ˆ	+	ˆ	+ ˆ
U1 U1		=U1		U1 =1, U 2			U	2	=U 2	U 2 =1.
Рассмотрим оператор			ˆ		ˆ	ˆ
			U	=U 2		U1 . Так как операция эрмитового

сопряжения означает комплексное сопряжение и транспонирование оператора, то при эрмитовом сопряжении произведения операторов каждый из них подвергается эрмитовому сопряжению, и они

ˆ

+

ˆ

ˆ

+

ˆ +

ˆ

+

.

располагаются в обратном порядке, т.е. U

=(U 2

U1 ) =U1

U

2

Тогда имеем

ˆ ˆ +

ˆ

ˆ

ˆ

+ ˆ

+

ˆ

ˆ ˆ +

ˆ

+

ˆ

ˆ

+

=1.

U U

=U

2 U1

(U1

U

2

)=U

2 (U1 U1

)U 2

=U 2

U 2

ˆ +

ˆ

Аналогичным способом получаем, что U

U =1. Таким образом,

ˆ

оператор U удовлетворяет условию унитарности.

8. Доказать,

что

оператор

сдвига

относительной

фазы

P(φ) ≡

0 0

+ei φ

1

1

является унитарным.

Доказательство

В вычислительном базисе { 0 , 1 } матрица оператора P(φ) является, очевидно, диагональной

P	P			1	0
00	01		=	0	ei φ .
P(φ) = P	P
10	11

106

Поэтому

1	0 1						0			1		0
P(φ) P(φ) + =			φ				−	φ		=				=1.
0	e	i			0	e	i				0	1

С методической точки зрения представляется полезным проверить выполнение условия унитарности непосредственным перемножением операторных выражений для P(φ) и P(φ) +. Тогда имеем

P(φ)P+ (φ) = ( 00 + eiφ 1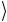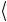1 )( 0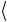0 + e−iφ 1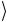1 ) = = 00 + 11 = 1.

На последнем шаге мы использовали условие полноты (2.6) базисных состояний, которое называют спектральным разложением единицы.

9. Доказать, что оператор Адамара H обладает следующими свойствами:

(а)	Н2 = 1
	Доказательство
	Воспользуемся выражением для Н через матрицы Пау-
	ли, т.е. Н=	1	(σ1 +σ3 ) .
	2

Тогда

Н2= 12 (σ1 +σ3 )2 = 12 (σ12 +σ32 +σ1σ3 +σ3σ1 ) = 1.

Здесь мы использовали свойство (2.45), т.е. σ12 =σ32 =1; а также свойство (2.46) антикоммутации разноименных матриц Паули, т.е. σ1σ3 = −σ3σ1 .

(б) Собственные значения λ оператора H равны

λ = ±1.

107

(в) Собственные состояния H, отвечающие этим собственным значениям, имеют вид

π

sin

π

cos

8

, u

8

u =

=

.

1

π

−1

−cos

π

sin

8

8

(г)

Унитарный оператор H есть преобразование пово-

G

1

1

рота спина на угол π вокруг оси n

=

, 0,

.

2

2

Указание

π

GG

GG

Записать H в виде H =σn = exp −i

exp

ˆ

.

iπ(sn)

2

10. Написать матрицу конечных вращений для спина 12 .

Решение

			Φ G G
ˆ	G	i	2 nσ
Оператор конечных вращений R(Φ, n) = e			представляет со-

бой экспоненциальную функцию от матриц Паули. Воспользуемся известным разложением экспоненты в ряд Тейлора

∞

k

e x = ∑

x

ˆ

k =0

k!

и запишем R в виде

ˆ

∞

(iΦ / 2)k G G

k

=

R

= ∑

k !

(nσ)

k =0

∞

(iΦ / 2)2s

GG

2s

∞

(iΦ / 2)2s+1 GG

2s+1

= ∑

(nσ)

+∑

(nσ)

,

(2s)!

(2s +1)!

s=0

s=0

108

где на последнем шаге вся сумма разбита на две части – по четным (k=2s) и нечетным (k=2s+1) значениям k. Рассмотрим величину

(nGσG)2 . С учетом свойства (2.44) имеем

(nGσG)2 = n jnkσ jσk = nj nk (δjk + iεjklσl ) = nG2 + i[nG×nG]σG =1,

так как

n2 =1, а [n ×n]=0.

Тогда

∞	(iΦ / 2)2s	GG 2		s	∞	(−1)s (Φ / 2)2s		Φ
∑		[(nσ)	]		= ∑		= cos		,
	(2s)!					(2s)!		2
s=0					s=0

и

∞	(iΦ / 2)2s+1 G G G G			2 s
∑		(nσ)[(nσ)		] =
	(2s +1)!
s=0
	G G ∞		(−1)s (Φ / 2)2s+1		G G	Φ
	= inσ	∑	(2s +1)!		= inσ sin		.
						2
		s=0

Здесь были использованы известные разложения функций cos x и sin x в ряд Тейлора.

Таким образом

			Φ G G
ˆ	G	i	2 nσ	= cos	Φ	G G	Φ
R(Φ, n) = e					2	+ inσ sin	2 .

Подставляя сюда явный вид матриц Паули и компоненты единичного вектора

n ={sin θcos φ,sin θsin φ, cos θ} ,

109

получаем матрицу
		Φ	+ inz sin		Φ
	cos
		2			2
ˆ
R(Φ, n) =					Φ
	i(nx + iny )sin
					2

i(nx −iny )sin Φ

2 =

cos Φ −inz sin Φ 2 2

		Φ		+i cosθsin			Φ
cos		2					2
=					Φ
	ie		i φ			sin θ
				sin	2

i e	−i φ		sin	Φ
				2	sinθ
	Φ							,
cos		−i cosθsin				Φ
	2					2

которая входит в формулу (2.68) и вместе с фазовыми множителем ei α определяет общий вид унитарной матрицы 2×2 .

11.

Вычислить

результирующую

матрицу

вращения

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

описывают вращение

R (β, γ,δ)

= Rz

(β)Ry (

γ)Rz

(δ), где Rz и

Ry

спина

1 2

вокруг осей z

и y

на углы,

указанные в аргументах.

Сравнить с выражением (2.70).

ˆ

происходит преобра-

12. То же самое, когда вместо вращения Ry

ˆ

зование Rx .

13. Найти явный вид операторов

σi

, где σi

– матрицы Паули.

Указание

Если взять, например,

преобразование вращения спина 1 2 вокруг

π

= iσ1

,

оси x на угол π, то exp i

2

σ1

π

π

−i π 1 + iσ

1

σ1

= exp

−i

exp i

σ1

= e

4

.

4

4

2

110