Теорема сложения

P A B P A P B P AB

P	n	Ai		n	P Ai		P		Ai Aj
	U
	i 1			i 1		1 i j n
	P			Ai Aj Ak ... 1 n 1 P						A1...An
1 i j k n

СФУ Т.В. Крупкина

21

Теорема умножения для двух событий

P AB P A P B | A	P B	P A | B ,

если соответствующие условные вероятности определены

(то есть если P(A) > 0, P(B) > 0).

Доказательство следует из определения условной вероятности.

СФУ Т.В. Крупкина

22

Теорема (формула полной вероятности)

Пусть A – случайное событие, H1, H2, …, Hn

– полная группа событий (гипотезы),

P Hi 0,	n
	A UHi .
	i 1

Тогда вероятность события А может быть вычислена по формуле:

n

P A P Hi P A | Hi

i 1

СФУ Т.В. Крупкина

23

Теорема (формула Байеса)

Пусть A – случайное событие, H1, H2, …, Hn

– полная группа событий (гипотезы),

	P Hi 0,		n
			A Hi .
			i 1
Тогда условная вероятность того, что имело
место событие Hk, если наблюдалось событие
А, может быть вычислена по формуле:
	P Hk | A	P Hk P A | Hk
		n
		P Hi P A | Hi
		i 1				24
		СФУ Т.В. Крупкина

Лекция 4. Схемы испытаний

Схемой испытаний Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода

— «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью p, а «неудача» — с вероятностью q = 1 – p.

СФУ Т.В. Крупкина

25

Теорема (формула Бернулли)

Обозначим через m число успехов в n испытаниях схемы Бернулли. Тогда

Pn m Cnm pmqn m

СФУ Т.В. Крупкина

26

Предельные теоремы для схемы Бернулли

При числе испытаний, превышающем 20, вычисление точного значения Pn(m) затруднительно. В этих случаях применяют приближенные формулы, вытекающие из предельных теорем.

Различают два случая:

когда р мало, используют приближение Пуассона,

когда р не мало (и не очень близко к единице),

справедливо приближение Муавра –Лапласа.

СФУ Т.В. Крупкина

27

Теорема Пуассона

Если при n , р 0 так, что np , 0 < < , то для любого фиксированного m N справедливо:

P m Cm pm 1 p n m p m me

n n m!

СФУ Т.В. Крупкина

28

Приближенная формула Пуассона

Pn m p m me m!

где = np. Приближенную формулу Пуассона применяют при

n > 30,

р< 0.1,

0.1< = np < 10.

СФУ Т.В. Крупкина

29

Локальная приближенная формула

Муавра –Лапласа

Pn m xm npq

x m np m 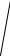npq

Локальную приближенную формулу Муавра –

Лапласа применяют при

n > 30, 0.1 p 0.9, nрq > 9.

СФУ Т.В. Крупкина

30

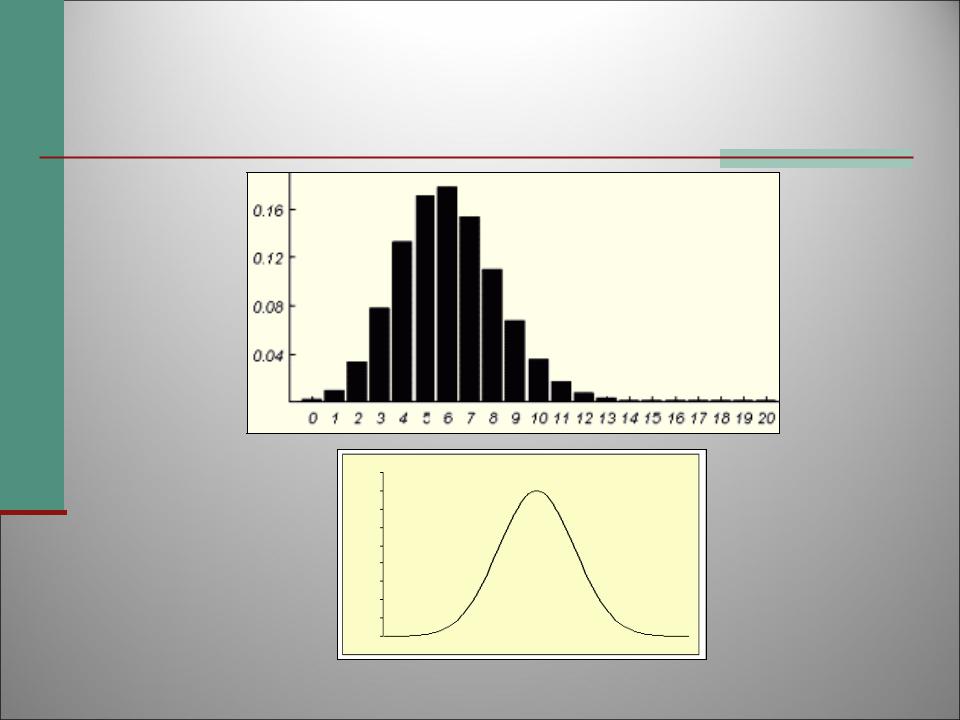
График биномиальных вероятностей при n=30, p=0,2 и график φ(X)

СФУ Т.В. Крупкина

31