В частности, если f(x,y) – многочлен, то уравнение (3.2) не имеет особых решений в области R.

Если в уравнении функция f(x,y) непрерывна по х и у и имеет частную производную по у, то особыми решениями могут быть те кривые y = ϕ(x) ,

∂f

во всех точках которых ∂y обращается в бесконечность

∂f		= ∞ .
∂y
		y=ϕ( x)

Будем называть такие кривые «подозрительными» на особое решение.

Пример 3. Найти кривую, «подозрительную» на особое решение уравнения dydx = 2 y и исследовать, будет ли она особым решением.

Решение. Общее решение данного уравнения имеет вид: y = (x +C)2 . Найдем кривую, «подозрительную» на особое решение, по виду правой

части.
Имеем:	∂f	=	1	= ∞.
	∂y		y	y=ϕ( x)

Ясно, что в качестве кривой y = ϕ(x) можно взять только y = 0 (ось ОХ). В каждой точке этого решения нарушается единственность решения задачи Коши. Возьмем любую точку (х0;0) на решении у = 0. Подставим координаты этой точки в общее решение; получим

0 = (x +C)2 C = −x0 .

Подставляя это значение С в общее решение, получим частное

решение y = (x − x )2	( x > x ).
0	0
Таким образом, через точку (х0;0) проходит не одна интегральная
кривая. Следовательно,	у = 0 -особое решение исходного уравнения. ■

4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, ИНТЕГРИРУЕМЫЕ В КВАДРАТУРАХ

Дифференциальное уравнение первого порядка, разрешённое относительно y′, имеет вид (ДУ (3.2))

	dy	= f (x, y) или dy − f (x, y)dx = 0.
	dx

8

Последнее уравнение является частным случаем уравнения
P(x, y)dx +Q(x, y)dy = 0 .	(4.1)

Дифференциальное уравнение первого порядка называется интегрируемым в квадратурах (или просто интегрируемым), если его общее решение может быть получено с помощью конечного числа элементарных (алгебраических) операций и квадратур. (Квадратурой называется операция отыскания первообразных.) Среди дифференциальных уравнений первого порядка, интегрируемых в квадратурах, рассмотрим некоторые виды ДУ первого порядка.

4.1. Дифференциальные уравнения с разделенными переменными

ДУ первого порядка (3.2) называется уравнением с разделенными переменными, если его можно представить в виде

f (x)dx + g( y)dy = 0 ,

(4.2)

в котором одно слагаемое f (x)dx зависит только от x, а другое g( y)dy

только от y. Для решения этого уравнения достаточно его проинтегрировать, получив общий интеграл уравнения (4.2):

∫ f (x)dx + ∫g( y)dy = С

или F(x) +G( y) = C ,

где F(x), G(y) – первообразные функций f(x), g(y) соответственно. Если последнее уравнение разрешить относительно y, то получится равенство y =ϕ(x, С) , правая часть которого является общим решением исходного уравнения (4.2).

Пример 1. Найти общее решение дифференциального уравнения

				2xdx +	dy			= 0 .
						y
Решение. Интегрируя, находим
				x2 + ln y = C .
Отсюда	ln y = C − х	2	и	с−х2		.
				у = е
Это равенство можно переписать в виде									у = ес е−х2 или (так как
ес = С )	у = С е−х2 . ■
1	1
Замечание. Поскольку нахождение								у	из общего интеграла может

представлять значительные трудности, но уже имеющие только алгебраический характер, то задачу решения ДУ считают законченной уже тогда, когда найден его общий интеграл. Более того, если общий интеграл

9

(или решение) уравнения выражен через неэлементарные интегралы, то и тогда уравнение считается решенным.

Например, 1) интегрируя уравнение 2xdx + (5y4 + cos y)dy = 0 , находим его общий интеграл x2 + y5 +sin y = C . Хотя выразить отсюда

у через х и С мы не сможем, но все же считаем исходное уравнение решенным.

2) Аналогично, записав для уравнения 2xdx + e−y2 dy = 0 общий интеграл x2 + ∫e−y2 dy = C , мы считаем, что решили уравнение, хотя интеграл ∫e−y2 dy и не выражается через элементарные функции.

4.2. Дифференциальные уравнения с разделяющимися переменными

Рассмотрим частный вид уравнения (4.1), а именно, когда функции P(x, y)и Q(x, y) представляют собой произведение функции, зависящей

только от х, на функцию, зависящую только от y , то есть
	P(x, y) =ϕ1	(x) ψ1( y),		(4.3)
	Q(x, y) =ϕ2 (x) ψ2 ( y).
Подставим (4.3) в ДУ	(4.1), получим
ϕ1(x) ψ1( y)dx +ϕ2		(x) ψ2 ( y)dy = 0.		(4.4)
Дифференциальное	уравнение	вида	(4.4)	называется
дифференциальным уравнением с разделяющимися переменными.

Разделив почленно уравнение (4.4) на ϕ2 (x) ψ1( y)				при условии, что
ϕ2 (x) ψ1( y) ≠ 0, получим уравнение с разделенными переменными:
ϕ1	(x) dx	+ψ2	( y) dy = 0 .	(4.5)
ϕ2	(x)	ψ1	( y)

Взяв неопределённые интегралы от обеих частей ДУ (4.5), получим общий интеграл данного уравнения:

∫ϕ1(x) dx + ∫ψ2 ( y) dy = С.

ϕ2 (x) ψ1( y)

Пример 1. Найти общее решение дифференциального уравнения

y′ =1 + x2 + y2 + x2 y2 .

Решение. Правая часть данного уравнения разлагается на множители

dydx = (1 + x2 ) (1 + y2 ) .

10

Поскольку (1+ y2 ) ≠ 0, обе части последнего уравнения разделим на

(1+ y2 ) и умножим на dx :

dy

= (1 + x2 ) dx ,

(1 + y2 )

интегрируя, получим

x3

∫

dy

= ∫(1+ x2 ) dx arctg y = x +

+C .

(1

+ y

2

)

3

Ответ: y = tg(x +

x3

+C).

■

3

Пример 2.

Решить задачу Коши для уравнения 3y2dy = xdx , если

y =1 при x = 2 .

Решение. Данное ДУ можно сразу интегрировать:

			3∫y2dy = ∫xdx y3 =			x2	+C .
				2
Учитывая начальные условия, найдём C :
			13 =	22	+С С = −1.
		x2		2
Ответ:	y3 =		−1. ■
	2

Многие ДУ могут быть приведены к виду уравнения с разделяющимися переменными путем замены переменных.

К числу таких уравнений относятся однородные дифференциальные уравнения первого порядка.

4.3. Однородные дифференциальные уравнения

Функция f (x, y) называется однородной измерения n , если для t

выполняется равенство f (tx,ty) = tn f (x, y) .
Дифференциальное уравнение первого порядка
P(x, y)dx +Q(x, y)dy = 0	(4.6)

называется однородным, если P(x, y) и Q(x, y) – однородные функции одного и того же измерения n , то есть

11

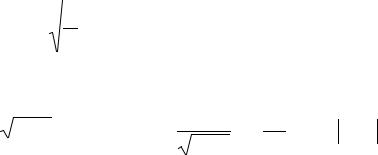
P(tx,ty) = tn P(x, y);

Q(tx,ty) = tnQ(x, y).

Однородное дифференциальное уравнение имеет вторую форму:

y′ =	y
	f		.	(4.7)
	x			y = zx
Дифференциальные уравнения			(4.6) и (4.7) заменой

приводятся к ДУ с разделяющимися переменными z и x , общий интеграл которых находится по методу интегрирования ДУ (4.4).

Пример 1. Найти общее решение уравнения xdy = (x + y)dx .

Решение. Это	уравнение однородное, так	как обе	функции
P(x, y) = x + y и	Q(x, y) = x – однородные	первого	измерения,
удовлетворяющие условиям
P(tx,ty) = tx +ty = t(x + y) = t1P(x, y),
Q(tx,ty) = tx = t1Q(x, y).
Пусть y = zx, тогда dy = zdx + xdz . Подставляя значения			y и dy в
исходное уравнение, получим

x(zdx + xdz) = (x + zx)dx.

После упрощения получим

xdz = dx .

Решаем полученное уравнение с разделяющимися переменными:

∫dz = ∫dx

z = ln

x

+C .

x

y

Возвращаясь к старой переменной ( z =

), получим

x

y

= ln

x

+C

y = x(ln

x

+C) .

x

Ответ. y = x(ln

x

+C) . ■

Пример 2. Решить задачу Коши для уравнения

xdy + (x

y −1

− y)dx = 0 , если y =1 при x =1.

x

Решение. Полагая

y = zx,

dy = zdx + xdz , придём к уравнению с

разделяющимися переменными:

dz

+ ∫dx = 0, z −1 ≠ 0

xdz + z −1dx = 0

∫

z −1

dx

12

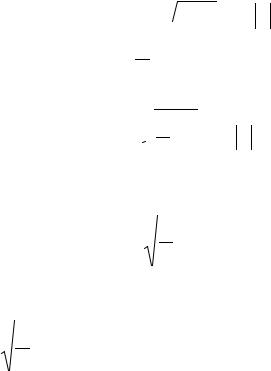
2 z −1 + ln x = C .

Заменяя значение z = xy , получим общее решение исходного

уравнения:

2 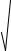xy −1 + ln x = C .

Учитывая начальное условие y(1) =1, находим частное решение данного уравнения

2

y

−1 + ln

x

= 0.

x

Если же z −1 = 0, то из подстановки y = zx получим y = x, (x ≠ 0) –

особое решение.

Ответ: 2

y

−1 + ln

x

= 0,

y = x. ■

x

4.4. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка

называется уравнение вида
y′+ P(x) y = Q(x),	(4.8)

в которое неизвестная функция и ее производная входят линейно (т.е. в первой степени).

Если Q(x) ≠ 0 , то уравнение (4.8) называется линейным неоднородным, если же Q(x) = 0 – линейным однородным.

Пусть P(x) ≠ 0, Q(x) ≠ 0 . Решение уравнения (4.8) будем искать в

виде произведения функций u = u(x), v = v(x), то есть

y = uv .

Так как одна функция выражается через две, то одной из двух функций мы можем управлять произвольно, как это удобно для решения, вторая функция будет зависеть от выбора первой.

Подставим

y = uv ,

dy

= u

dv

+ v

du

в ДУ

(4.8).

dx

dx

dx

Тогда

u

dv

+ v

du

+ Р(x)uv = Q(x)

или

dx

dx

dv

du

u

+ v

+

Р(x)u

= Q(x) .

(4.9)

dx

dx

13

Выберем функцию u так, чтобы в уравнении (4.9) обратился в нуль

коэффициент при функции v , то есть чтобы
			du	+ Р(x)u = 0.					(4.10)
			dx
ДУ (4.10) –		с разделяющимися переменными. Решая							его, получим
(при u ≠ 0 )
∫	du	= −∫P(x)dx ln				u		= −∫P(x)dx
	u
		u(x) = e−∫ P( x)dx							(4.11)

Мы берём какое-либо частное решение ДУ (4.10), а не общее, так как нам достаточно подобрать одну функцию u(x) . Подставляя найденное

значение u(x)

из (4.11) в (4.9), получаем ДУ с разделяющимися

переменными для определения функции				v(x) :
e	−∫ P( x)dx		dv	= Q(x) .
			dx
Откуда находим общее решение v(x)
v(x) = ∫Q(x) e∫ P( x)dxdx +C .					(4.12)

Окончательно, общее решение линейного уравнения (4.8):

y = uv = e−∫ P( x)dx [ Q(x)e∫ P( x)dxdx + C].						(4.13)
					∫
Пример 1. Найти общее решение уравнения
	dy	−	2		y = (x +1)3 .
			x +1
	dx

Решение. Для решения можно было бы воспользоваться готовой формулой (4.13), но она сложна для запоминания, поэтому при решении кратко повторим все выкладки общего случая.

Полагаем y = uv ,

тогда

dy

= u

dv

+ v

du

. Подставляем значения y и

dx

dx

dx

dy в данное уравнение, получим

u

dv

+ v

du

−

2

uv = (x +1)3

x +1

dx

dx

dv

du

2

или

u

+ v

−

u = (x +1)3 .

(*)

dx

x +1

dx

Выберем функцию u так, чтобы коэффициент при v(x)

обратился в

нуль:

14