§6. Добутки векторів

6.1. Скалярний добуток векторів

Означення скалярного добутку. Скалярним добутком двох ненульових векторів іназивається число, що дорівнює добутку довжин цих векторів на косинус кута між ними.

Якщо хоча б один із двох даних векторів нульовий, то їх скалярний добуток за означенням вважається рівним нулю.

Позначається або , або. Таким чином, за означенням,

, (6.1)

де .

Так як є проекцією вектора на вектор , а – проекцією вектора на вектор , то формулі (6.1) можна надати іншого вигляду:

, (6.2)

тобто скалярний добуток рівний добутку довжини одного з них на проекцію іншого на перший вектор.

Властивості скалярного добутку.

1. .

Справедливість цієї властивості випливає з означення.

2. .

Доведення. .

3. .

Доведення.

.

4. Скалярний квадрат вектора рівний квадрату його довжини:

.

Доведення. .

Зокрема, .

Якщо добути корінь із скалярного квадрата вектора, то отримаємо не початковий вектор, а його модуль , тобто.

5. Якщо ненульові вектори і ортогональні, то їх скалярний добуток рівний нулю і навпаки, якщо скалярний добуток двох ненульових векторів рівний нулю, то ці вектори ортогональні.

Доведення. Так як , то, а отже і.

Якщо і , , то і.

Зокрема, .

Приклад 6.1. Знайти , якщо ,, , ,

.

Розв’язок.

. 

Приклад 6.2. Знайти довжину вектора , якщо , ,

.

Розв’язок.



Скалярний добуток в координатній формі. Нехай в декартовій прямокутній системі координат задані вектори ,або, що те ж саме,,.

Знайдемо скалярний добуток цих векторів, перемноживши їх як многочлени згідно властивостям 1 – 3:

.

Згідно властивостям 4, 5, отримаємо:

. (6.3)

Таким чином, скалярний добуток векторів рівний сумі добутків їх однойменних координат.

За формулою (6.3) маємо

, (6.4)

звідки

. (6.5)

Приклад 6.3. Знайти довжину вектора .

Розв’язок. 

Нехай в декартовій прямокутній системі координат задані точки ,.

Відстань між двома точками ірівна

. (6.6)

Так як , токут між ненульовими векторами івизначається за формулами:

,

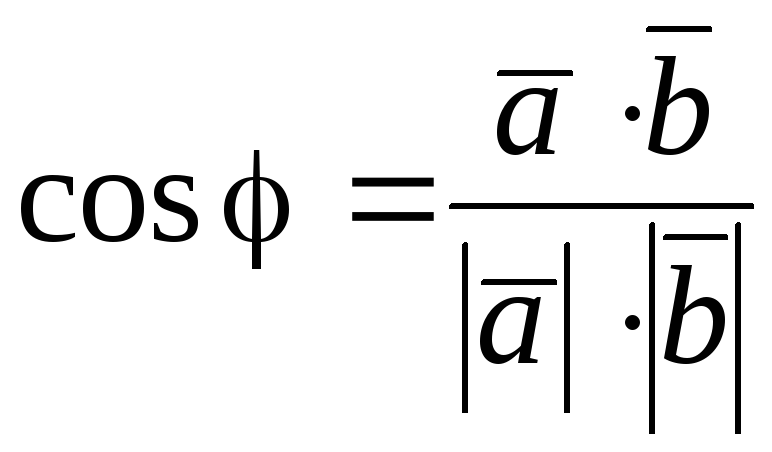тобто

. (6.7)

З останньої формули випливає умова перпендикулярності ненульових векторів і:

. (6.8)

Нехай кути, які утворює вектор з осями координат ,,, відповідно рівні. Тоді проекції вектора на осі координат рівні

, ,. (6.9)

Звідси

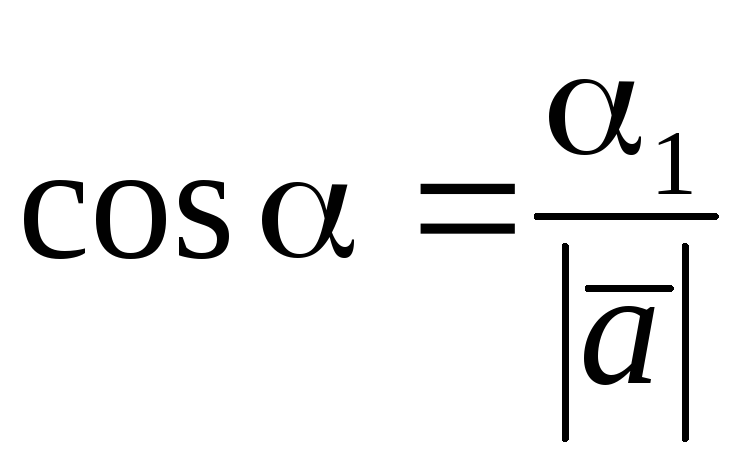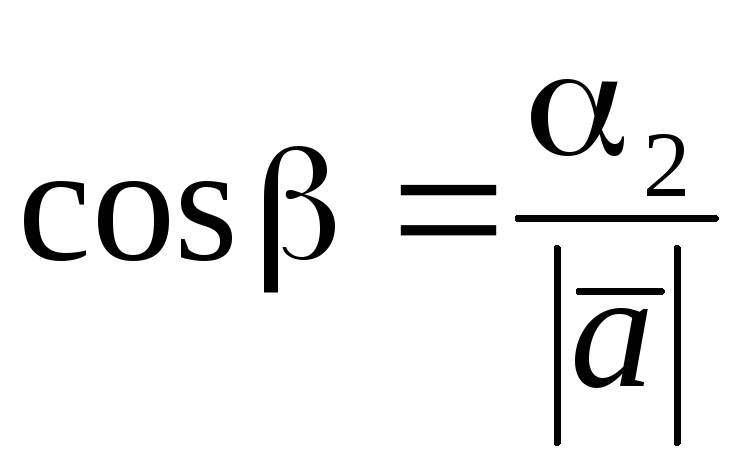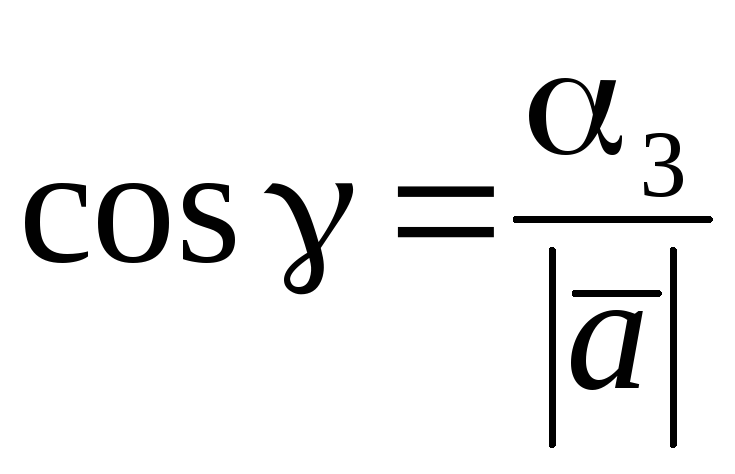, ,. (6.10)

Числа ,,називаютьсянапрямними косинусами вектора .

Підставивши вирази (6.9) в рівність (6.4), отримаємо

.

Скоротивши на , отримаємо співвідношення

.

Приклад 6.4. Довести, що діагоналі чотирикутника, заданого координатами вершин ,,,, взаємно перпендикулярні.

Розв’язок. Складемо вектори і, що лежать на діагоналях даного чотирикутника:

; .

Знайдемо скалярний добуток цих векторів:

.

Згідно властивості 5, вектори іперпендикулярні, що й треба було довести.

Приклад 6.5. Дано трикутник з вершинами в точках ,,. Знайти проекцію сторонина сторону.

Розв’язок. Складемо вектори і, що лежать на сторонах даного трикутника:

; .

З формули (6.2) знаходимо

. 

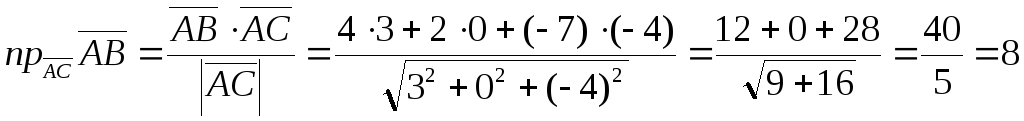Приклад 6.6. Знайти кут між векторами і, якщо,.

Розв’язок. За формулою (6.7) знаходимо

,

. 

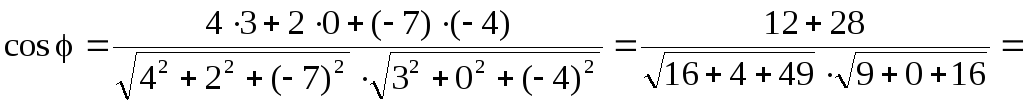
Приклад 6.7. Знайти напрямні косинуси вектора , якщо,.

Розв’язок. Знайдемо координати і довжину вектора :

,

.

За формулами (6.10)

, ,.