4.3. Розв’язання довільних лінійних систем. Теорема Кронекера-Капеллі

Нехай дана довільна система т лінійних рівнянь з п невідомими

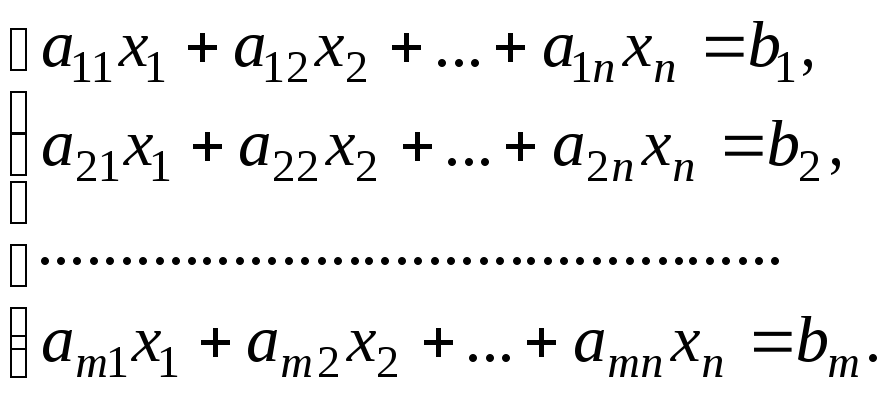
Відповідь на питання щодо сумісності цієї системи дає терема Кронекера-Капеллі:

Теорема 4.1. Система лінійних алгебраїчних рівнянь сумісна тоді і тільки тоді, коли ранг розширеної матриці системи рівний рангу основної матриці.

Приймемо її без доведення.

Правила знаходження всіх розв’язків сумісної системи лінійних рівнянь випливають з наступних теорем:

Теорема 4.2. Якщо ранг сумісної системи рівний кількості невідомих, то система має єдиний розв’язок.

Теорема 4.3. Якщо ранг сумісної системи менший кількості невідомих, то система має безліч розв’язків.

Правило розв’язання довільних лінійних систем.

1. Знайти ранги основної і розширеної матриць системи. Якщо 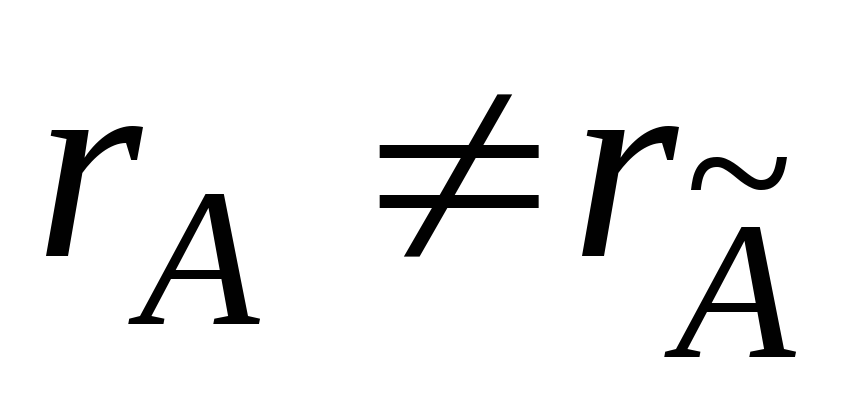, то система несумісна.

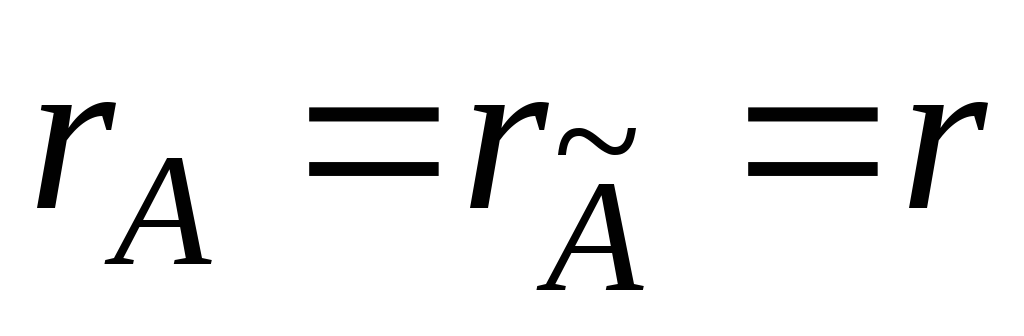2. Якщо , то система сумісна. Знайти базисний мінор порядку. Взяти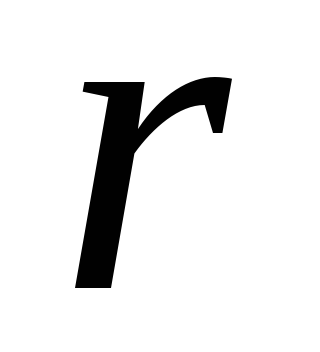рівнянь, з коефіцієнтів яких складений базисний мінор (інші рівняння відкинути). Невідомі, коефіцієнти при яких входять в базисний мінор, називаютьбазисними або основними і залишають зліва, а інші 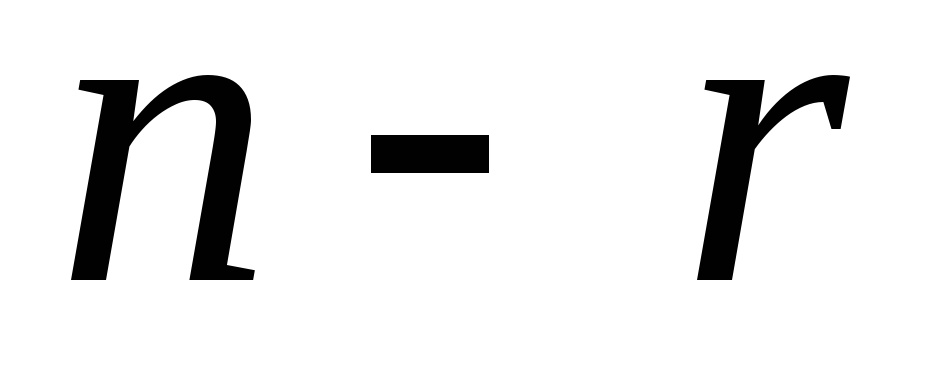невідомих називаютьвільними або неосновними і переносять в праві частини рівнянь.

3. Виразити базисні невідомі через вільні. Отримаємо загальний розв’язок системи.

4. Надаючи вільним невідомим довільних значень, отримаємо відповідні значення базисних невідомих. Таким чином можна знайти частинні розв’язки системи рівнянь.

4.4. Розв’язання лінійних систем методом Гауса

Універсальним методом розв’язання систем лінійних алгебраїчних рівнянь є метод Гауса, який полягає в послідовному виключенні змінних.

Нехай дана система т лінійних рівнянь з п невідомими

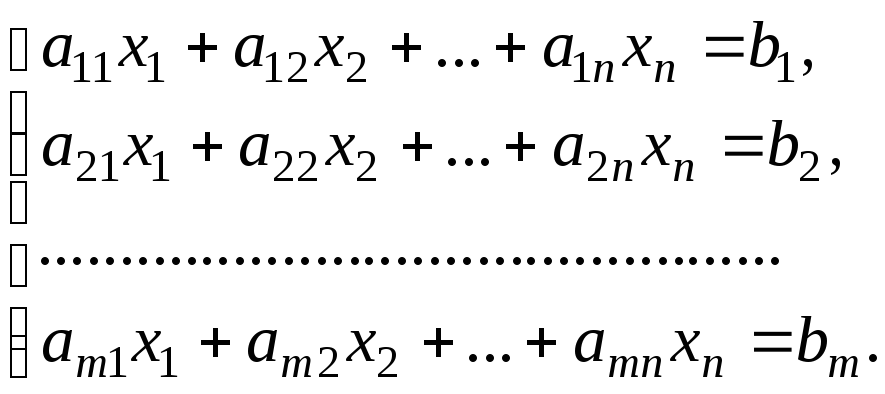(4.6)

Процес розв’язання за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система зводиться до ступінчастого (зокрема, до трикутного) вигляду.

Наведена нижче система має ступеневий вигляд:

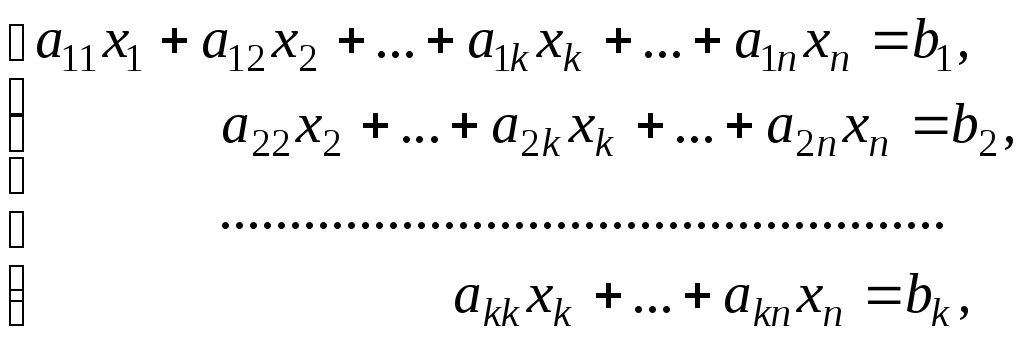
де .

На другому етапі (обернений хід ) йде послідовне знаходження невідомих з цієї ступінчастої системи.

Опишемо метод Гауса детальніше.

Прямий хід.

Вважатимемо, що елемент (якщо, то першим в системі запишемо рівняння, в якому коефіцієнт привідмінний від нуля ).

Перетворимо систему (4.6), виключивши невідому з усіх рівнянь, крім першого, використовуючи елементарні перетворення системи. Для цього помножимо обидві частини першого рівняння наі додамо почленно до другого рівняння системи. Потім помножимо обидві частини першого рівняння наі додамо до третього рівняння системи. Продовжуючи цей процес, отримаємо еквівалентну систему

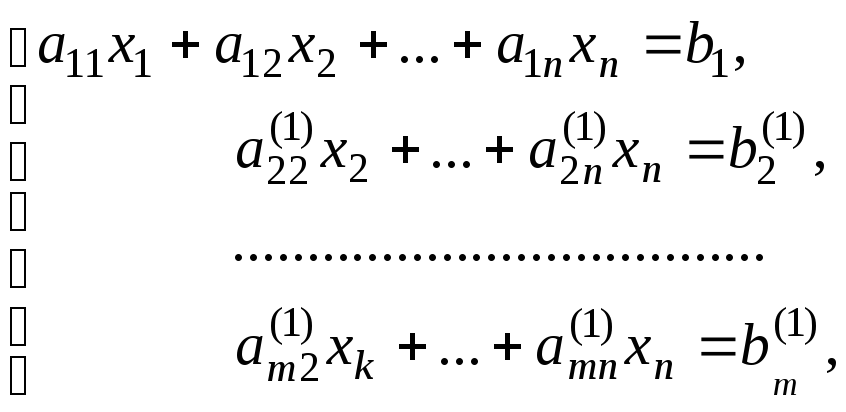
де – нові значення коефіцієнтів і вільних членів, які отримуються після першого кроку.

Аналогічно, вважаючи , виключаємо невідомуз усіх рівнянь системи, крім першого і другого, і так далі. Продовжуємо цей процес поки це можливо.

Якщо в процесі приведення системи (4.6) до ступінчастого вигляду з’являться нульові рівняння, тобто рівняння вигляду , то їх відкидаємо. Якщо ж з’являться рівняння вигляду, то система несумісна.

Обернений хід.

Розв’язуємо ступінчасту систему, яка, взагалі, має безліч розв’язків. В останньому рівнянні цієї системи виражаємо першу невідому через інші невідомі. Потім підставляємо значенняв передостаннє рівняння системи і виражаємо невідомучерез невідомі; потім знаходимо. Надаючи вільним невідомимдовільних значень, отримаємо безліч розв’язків системи.

Зауваження.

1. Якщо ступінчаста система виявиться трикутною, тобто 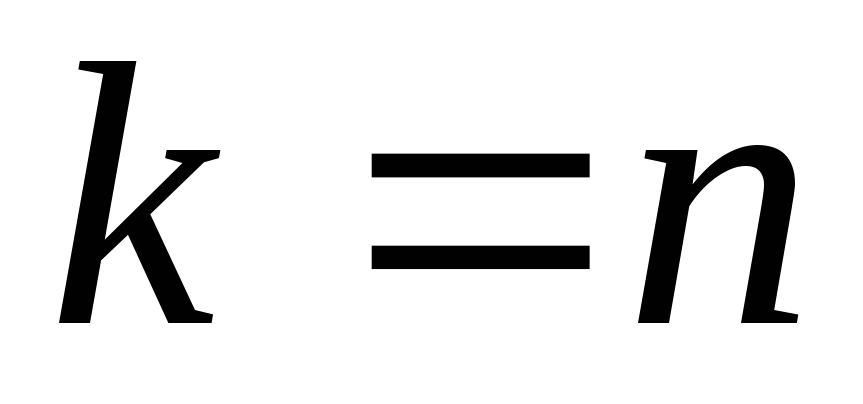, то початкова система має єдиний розв’язок. З останнього рівняння знаходимо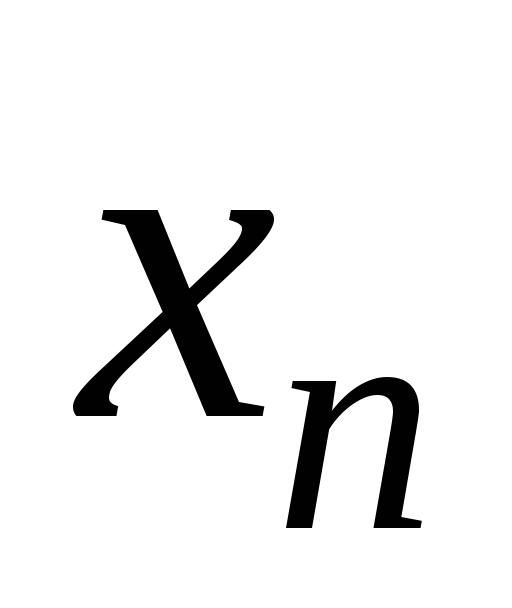, з передостаннього рівняння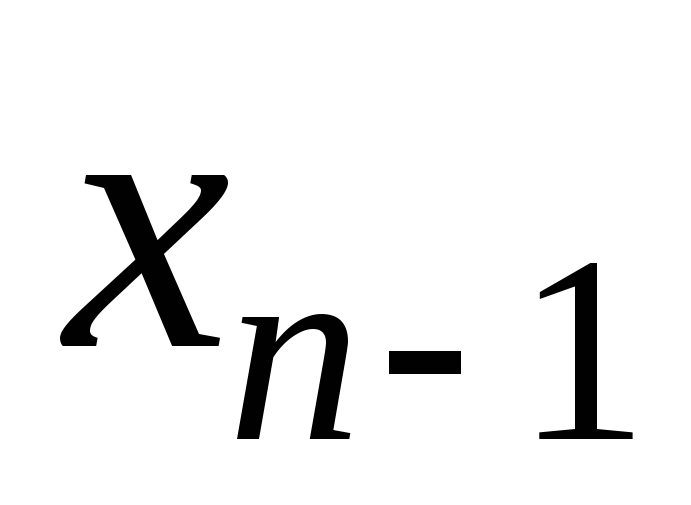, далі, піднімаючись по системі вверх, знаходимо всі інші невідомі.

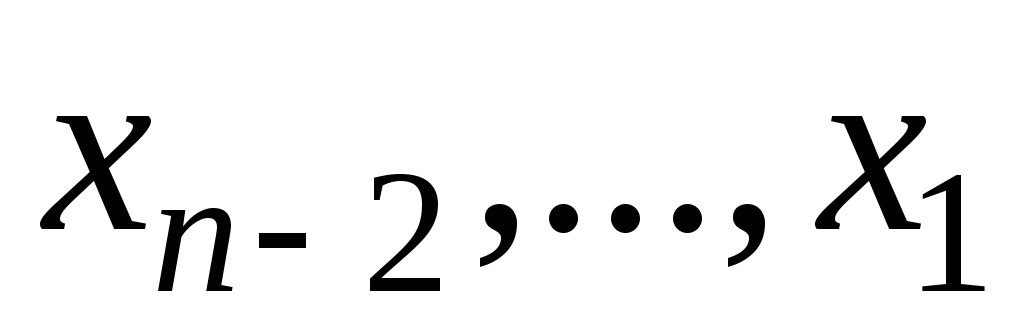2. На практиці зручно замість перетворень системи виконувати елементарні перетворення над рядками розширеної матриці системи, тобто приводити її до трапецієвидного вигляду. Зручно, щоб коефіцієнт 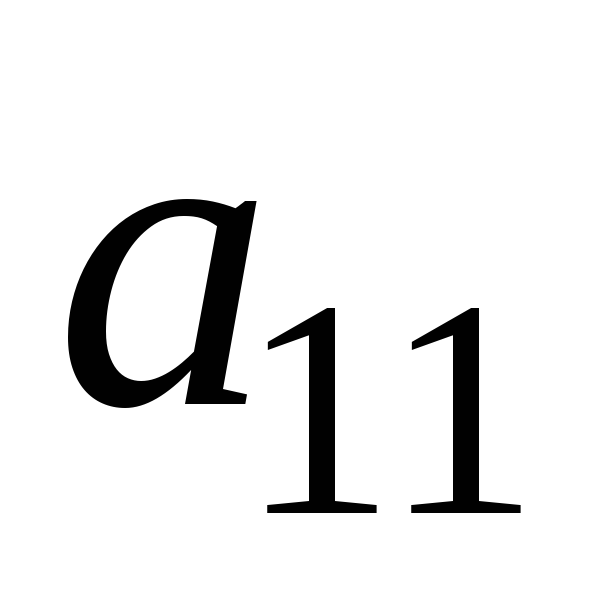дорівнювавабо(переставляємо рядки або множимо рядок на).

Теоретичні питання

1. Яка система називається лінійною?

2. Що називається основною матрицею і розширеною матрицею системи т лінійних рівнянь з п невідомими?

3. Що називається розв’язком системи т лінійних рівнянь з п невідомими?

4. Яка система лінійних рівнянь називається сумісною і яка – несумісною?

5. Яка система лінійних рівнянь називається визначеною і яка – невизначеною?

6. Які системи називаються еквівалентними?

7. Яка система лінійних рівнянь називається однорідною?

8. Які перетворення системи називають елементарними?

9. Яка система лінійних рівнянь називається невиродженою і яка – виродженою?

10. Скільки розв’язків має невироджена система?

11. Запишіть в матричному вигляді розв’язок невиродженої системи .

12. Запишіть формули Крамера.

13. Сформулюйте теорему Кронекера-Капеллі.

14. В якому випадку система лінійних рівнянь має єдиний розв’язок?

15. В якому випадку система лінійних рівнянь має безліч розв’язків?

16. Яке правило розв’язання довільних лінійних систем?

17. В чому полягає метод Гауса?

Задачі та вправи

В задачах 4.1–4.2 розв’язати системи: а) матричним способом; б) за формулами Крамера.

4.1.

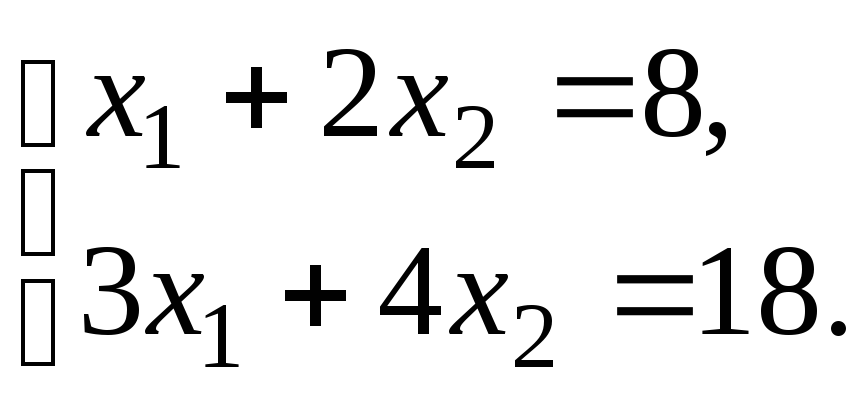
4.2.

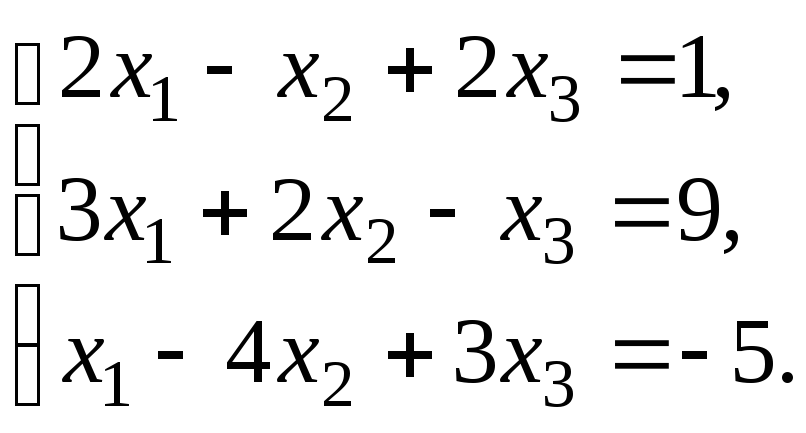
4.3. Розв’язати систему:

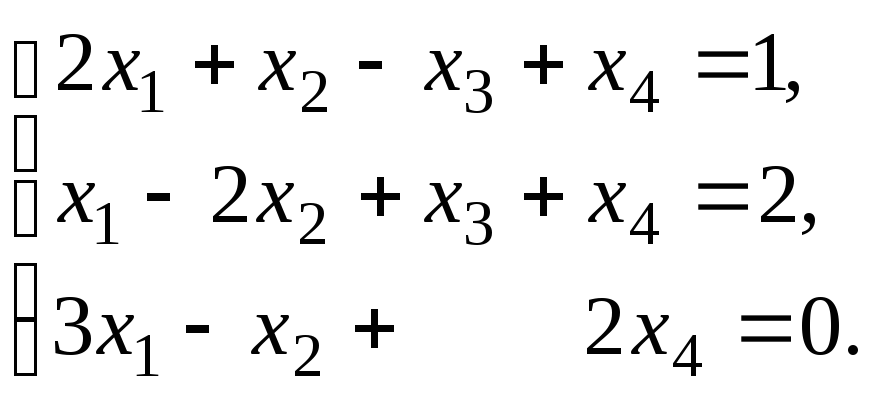
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

Отримали . Так як, то система несумісна. 

4.4. Розв’язати систему:

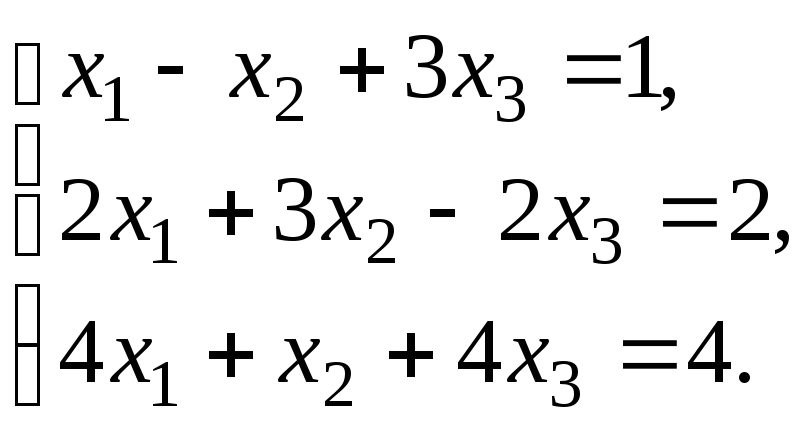
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

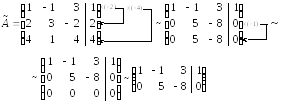
Отримали . Отже, система сумісна.

Кількість невідомих – .

Так як , то система має безлічрозв’язків.

В якості базисного мінора можна взяти, наприклад, мінор

.

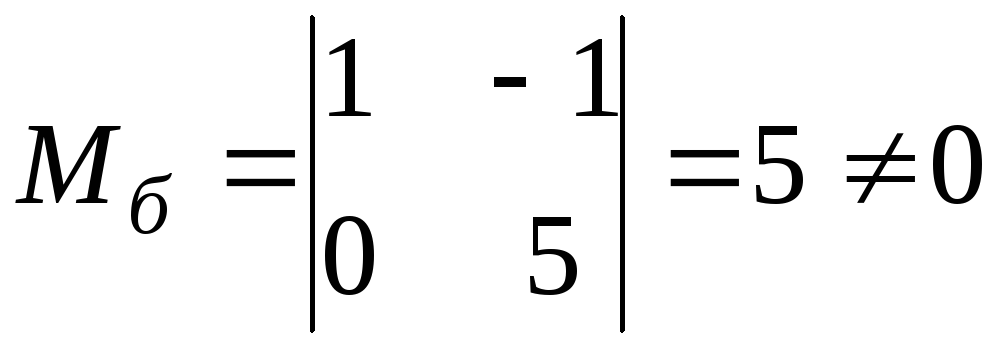Тоді базисними будуть невідомі , а– вільна.

Дана система еквівалентна системі:

або

За методом Гауса знаходимо

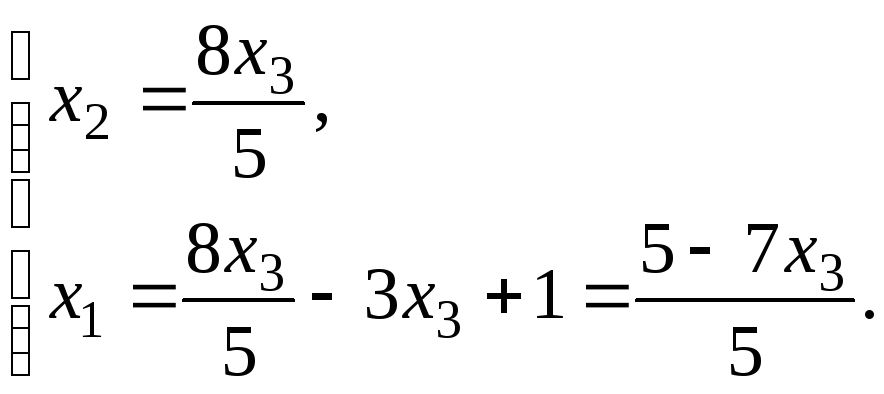
Покладемо , тоді множина розв’язків системи має вигляд

.

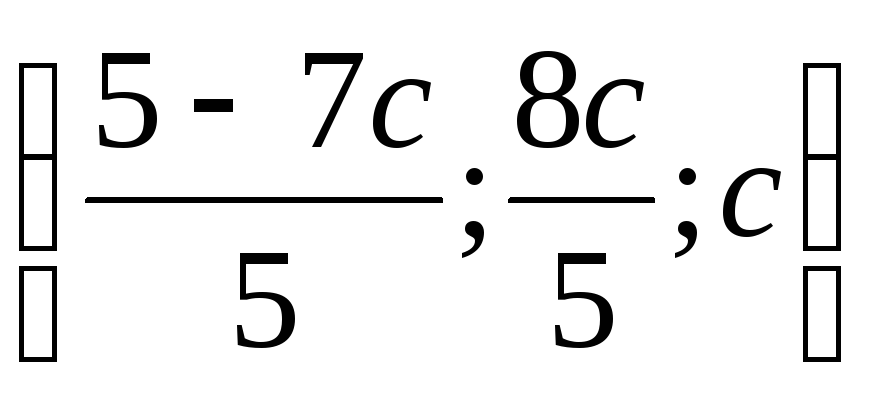Перевірка:

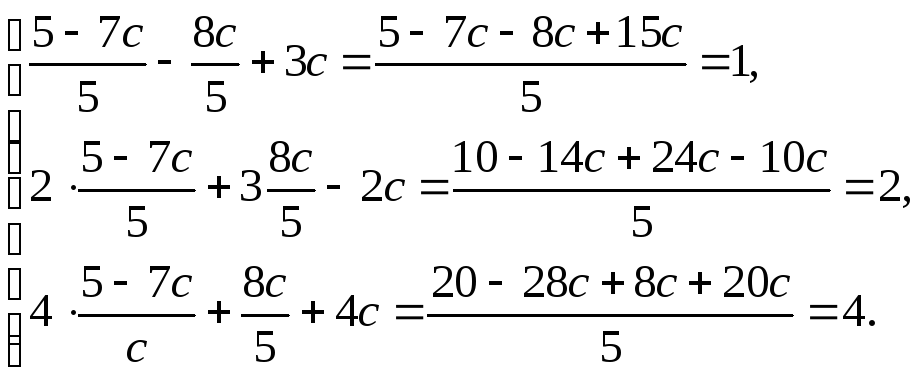
Відповідь: .

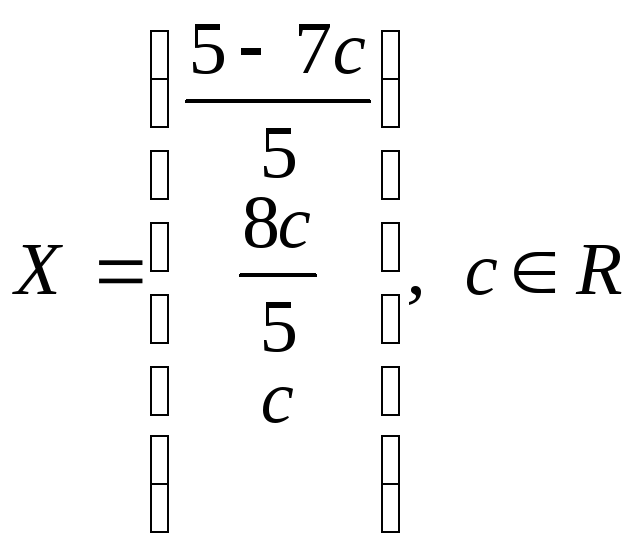4.5. Розв’язати систему:

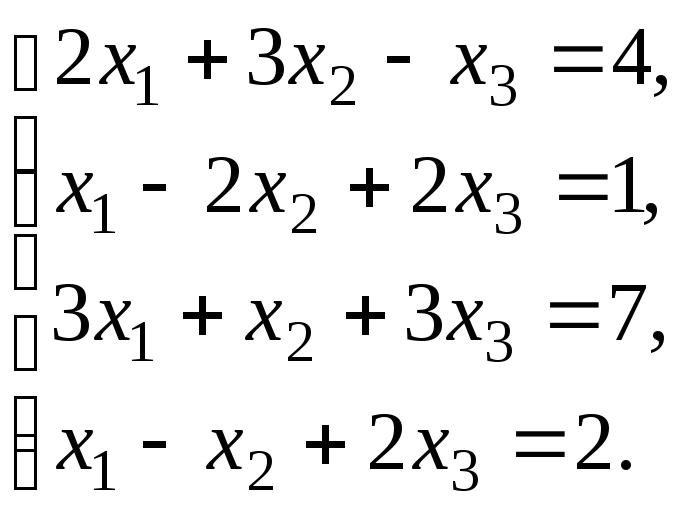
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

Отримали . Отже, система сумісна.

Кількість невідомих – .

Так як , то система має єдинийрозв’язок.

Дана система еквівалентна системі:

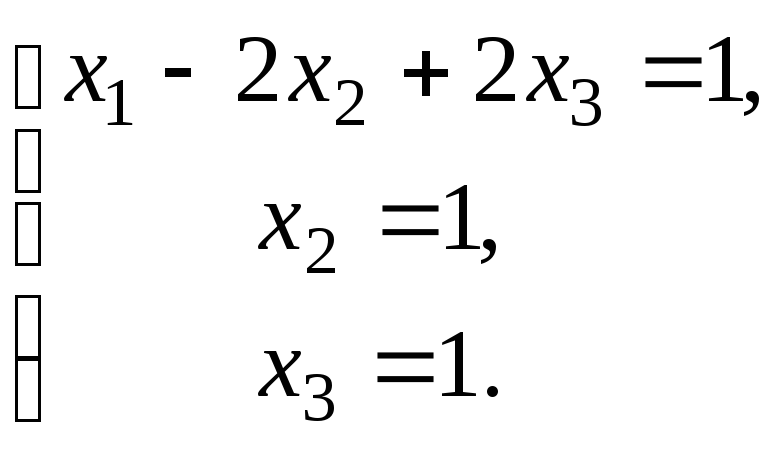
За методом Гауса знаходимо

.

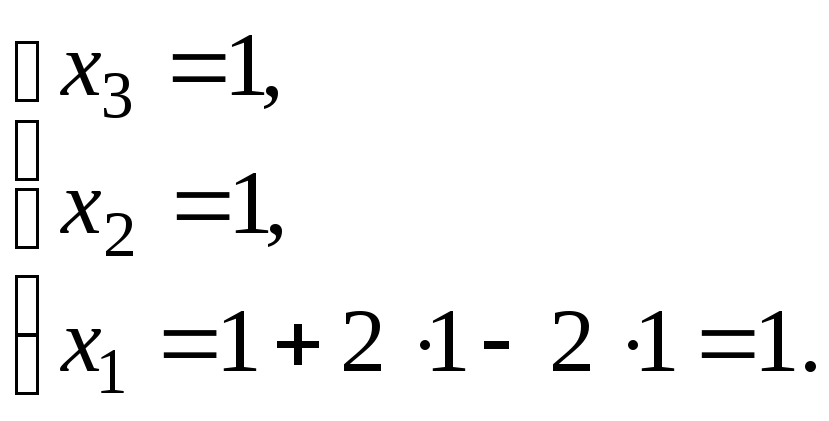Перевірка:

Відповідь: .

4.6. Розв’язати систему методом Гауса:

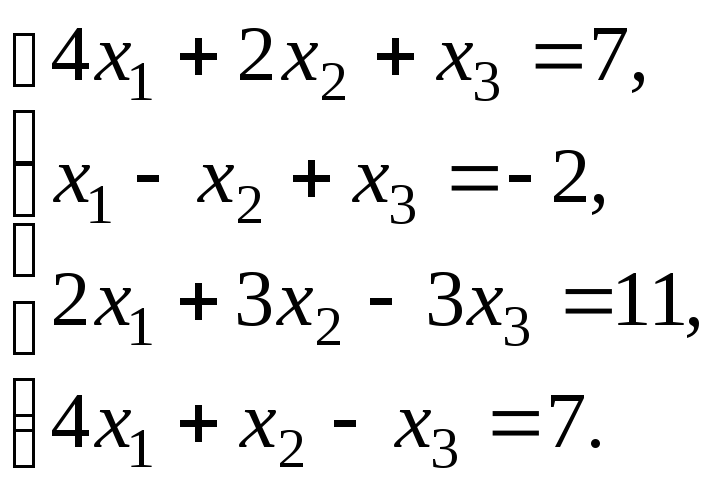
Розв’язок.

Прямий хід. За допомогою елементарних перетворень зведемо розширену матрицю системи до трапецієвидного вигляду:

Цій матриці відповідає система:

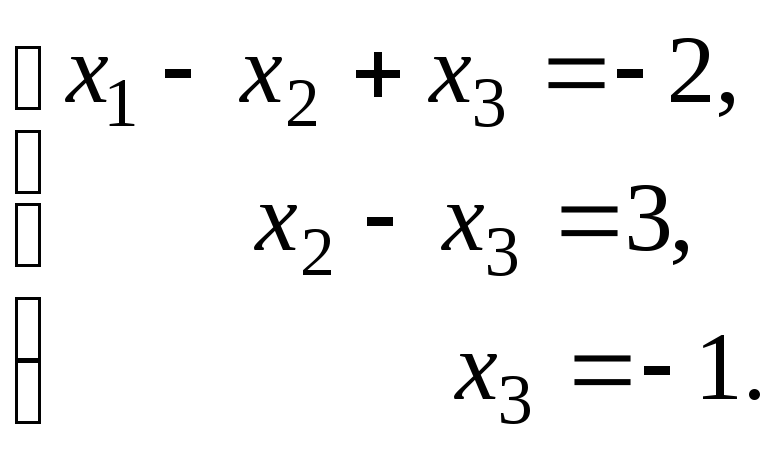
Обернений хід. Знаходимо

.

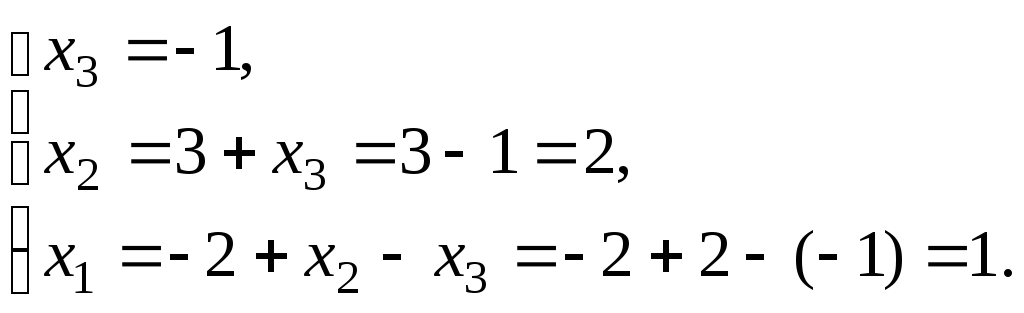Перевірка:

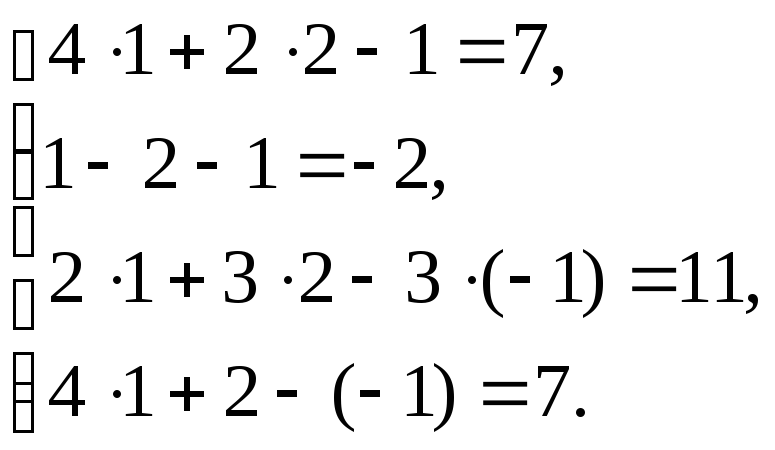
Відповідь: .

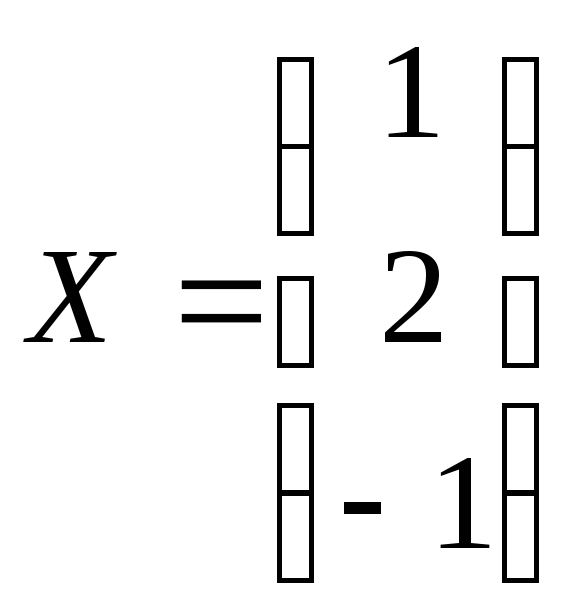Розділ ІI. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ

Лекція 5