
- •Конспект лекцій з курсу лінійної алгебри та аналітичної геометрії
- •Організація навчального процесу за кредитно-модульною системою
- •§1. Матриці
- •1.1. Основні поняття
- •1.2. Дії над матрицями
- •1.3. Транспонування матриць
- •§2. Визначники
- •2.1. Основні поняття
- •2.2. Властивості визначників
- •§3. Невироджені матриці
- •3.1. Основні поняття
- •3.2. Обернена матриця
- •3.3. Ранг матриці
- •§4. Системи лінійних рівнянь
- •4.1. Основні поняття
- •4.2. Розв’язання невироджених лінійних систем
- •4.3. Розв’язання довільних лінійних систем. Теорема Кронекера-Капеллі
- •4.4. Розв’язання лінійних систем методом Гауса
- •§5. Вектори
- •5.1. Основні поняття
- •5.2. Лінійні операції над векторами
- •5.3. Розклад вектора за базисом
- •5.4. Лінійні операції над векторами в координатній формі
- •5.5. Декартова прямокутна система координат
- •5.6. Поділ відрізка в даному відношенні
- •§6. Добутки векторів
- •6.1. Скалярний добуток векторів
- •6.2. Векторний добуток векторів
- •6.3. Мішаний добуток векторів
- •§7. Лінії на площині, поверхні і лінії в просторі
- •7.1. Рівняння лінії на площині
- •7.2. Рівняння поверхні та лінії в просторі
- •§8. Площина, пряма в просторі і на площині
- •8.1. Загальне рівняння площини
- •8.2. Загальне рівняння прямої на площині
- •8.3. Канонічні і параметричні рівняння прямої. Рівняння прямої з кутовим коефіцієнтом
- •8.4. Загальні рівняння прямої в просторі
- •8.5. Рівняння прямої, що проходить через дві точки
- •8.6. Рівняння площини, що проходить через три точки
- •8.7. Кут між площинами, кут між прямими, кут між прямою і площиною
- •8.8. Відстань від точки до площини і від точки до прямої на площині
- •8.9. Умова, при якій дві прямі лежать в одній площині
- •Пряма на площині
- •Площина
- •Пряма в просторі. Пряма і площина
- •§9. Лінії другого порядку
- •9.1. Еліпс
- •9.2. Гіпербола
- •9.3. Парабола
- •9.4. Еліпс, гіпербола, парабола з осями, паралельними осям координат
- •Відповіді
- •8.11. . 8.12.. 8.13..
- •8.15. . 8.16.. 8.17..
- •Індивідуальні завдання
- •Тестові завдання з лінійної алгебри
- •Відповіді
- •Тестові завдання з аналітичної геометрії
- •Відповіді
9.2. Гіпербола
Канонічне рівняння гіперболи. Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох даних точок цієї площини є сталою величиною, меншою від відстані між даними точками. Дані точки називаються фокусами.
Позначимо
фокуси через
![]() ,
,![]() ,
відстань між ними
,
відстань між ними![]() ,
а модуль різниці відстаней від будь-якої
точки гіперболи до його фокусів – через
,
а модуль різниці відстаней від будь-якої
точки гіперболи до його фокусів – через![]() .
Згідно означенню гіперболи
.
Згідно означенню гіперболи![]() .
.
Для
виведення рівняння гіперболи виберемо
систему координат
![]() так, щоб фокуси
так, щоб фокуси![]() ,
,![]() лежали на осі
лежали на осі![]() ,
а початок координат співпадав з серединою
відрізка
,
а початок координат співпадав з серединою
відрізка![]() (рис. 9.4). Тоді фокуси матимуть координати
(рис. 9.4). Тоді фокуси матимуть координати![]() ,
,![]() .
.
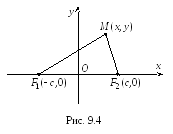
Нехай
![]() – довільна точка гіперболи. За означенням
для довільної точки гіперболи і тільки
для точок гіперболи справедлива рівність:
– довільна точка гіперболи. За означенням
для довільної точки гіперболи і тільки
для точок гіперболи справедлива рівність:
![]() або
або
![]() ,
,
тобто
![]()
– це і є рівняння гіперболи. Приведемо отримане рівняння до більш простого вигляду, як це було зроблено для еліпса. Отримаємо:
![]() .
.
Так як
![]() ,
то
,
то![]() .
Ввівши позначення
.
Ввівши позначення![]() ,
отримаємо:
,
отримаємо:![]() або
або
![]() (9.4)
(9.4)
Можна довести, що рівняння (9.4) рівносильне початковому рівнянню. Воно називається канонічним рівнянням гіперболи.
Дослідження
форми гіперболи за її рівнянням.
Координати
![]() і
і![]() входять в рівняння (9.4) в парних степенях,
тому гіпербола симетрична відносно
осей координат і відносно початку
координат.
входять в рівняння (9.4) в парних степенях,
тому гіпербола симетрична відносно
осей координат і відносно початку
координат.
Для
точок, що лежать в першій координатній
чверті (![]() )
маємо
)
маємо
![]() .
.
З цієї
рівності випливає, що
![]()
![]()
![]() .
При
.
При![]() :
:![]() .
При зростанні
.
При зростанні![]() значення
значення![]() теж зростають, і точка
теж зростають, і точка![]() кривої при цьому необмежено віддаляється
від осей
кривої при цьому необмежено віддаляється
від осей![]() і
і![]() .
.
Побудуємо гіперболу в першій координатній чверті і, враховуючи симетрію, відобразимо побудовану частину відносно осей координат (рис. 9.5). Гіпербола складається з двох частин, які називаються вітками.

Центр
симетрії
![]() називаютьцентром
гіперболи.
Точки
називаютьцентром
гіперболи.
Точки
![]()
![]() – точки перетину гіперболи з віссю
– точки перетину гіперболи з віссю![]() називаютьвершинами
гіперболи.
З віссю
називаютьвершинами
гіперболи.
З віссю
![]() гіпербола не перетинається. Відрізок
гіпербола не перетинається. Відрізок![]() ,
а також його довжина
,
а також його довжина![]() називаютьсядійсною
віссю
гіперболи,
а число
називаютьсядійсною
віссю
гіперболи,
а число
![]() –уявною
віссю гіперболи.
–уявною
віссю гіперболи.

Рівняння
![]() теж є рівнянням гіперболи. Фокуси такої
гіперболи лежать на осі
теж є рівнянням гіперболи. Фокуси такої
гіперболи лежать на осі![]() (рис. 9.6). В цьому випадку точки
(рис. 9.6). В цьому випадку точки![]()
![]() євершинами
гіперболи,
а
євершинами
гіперболи,
а
![]() –дійсною
віссю,
–дійсною
віссю,
![]() –уявною.
–уявною.
Якщо
![]() ,
то гіпербола називаєтьсярівносторонньою.
,
то гіпербола називаєтьсярівносторонньою.
Асимптоти
гіперболи. Пряма
![]() називаєтьсяасимптотою
необмеженої
кривої
називаєтьсяасимптотою
необмеженої
кривої
![]() ,
якщо відстань
,
якщо відстань![]() від точки
від точки![]() кривої
кривої![]() до цієї прямої прямує до нуля при
необмеженому віддаленні точки
до цієї прямої прямує до нуля при
необмеженому віддаленні точки![]() вздовж кривої
вздовж кривої![]() від початку координат (рис. 9.7).
від початку координат (рис. 9.7).
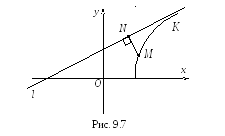
Покажемо, що гіпербола, задана рівнянням (9.4), має дві асимптоти:
![]() і
і
![]() .
(9.5)
.
(9.5)
Так як прямі (9.5) і гіпербола (9.4) симетричні відносно осей координат, то достатньо розглянути тільки ті їх точки, що лежать в першій координатній чверті.
Візьмемо
на прямій
![]() точку
точку![]() з такою ж абсцисою
з такою ж абсцисою![]() ,
як і в точки
,
як і в точки![]() ,
що лежить на гіперболі
,
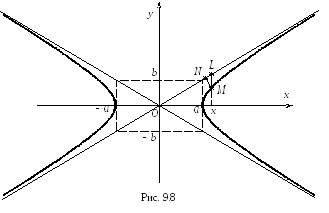
що лежить на гіперболі![]() (рис. 9.8) і знайдемо різницю
(рис. 9.8) і знайдемо різницю![]() між ординатами прямої і вітки гіперболи:
між ординатами прямої і вітки гіперболи:
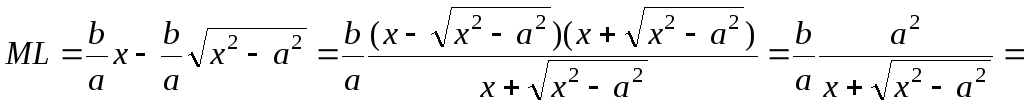
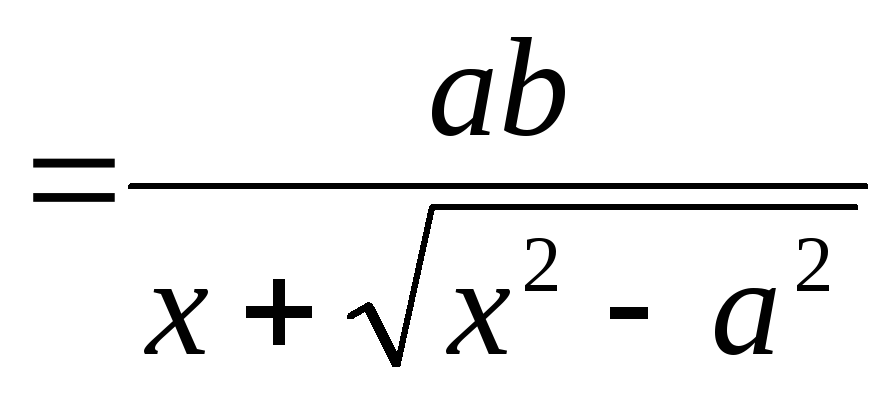 .
.
Чисельник
отриманого дробу є постійною величиною,
а знаменник збільшується при зростанні
![]() .
Отже, довжина відрізка
.
Отже, довжина відрізка![]() прямує до нуля при
прямує до нуля при![]() .
Так як
.
Так як![]() ,
то
,
то![]() теж прямує до нуля. Таким чином, прямі
теж прямує до нуля. Таким чином, прямі
![]()
є асимптотами гіперболи.
Для
гіперболи, заданої рівнянням
![]() ,
асимптоти також мають вигляд (9.5).
,
асимптоти також мають вигляд (9.5).
При
побудові гіперболи доцільно спочатку
побудувати прямокутник з центром
симетрії в початку координат із сторонами
![]() ,
,![]() .
Прямі, що проходять через протилежні
вершини цього прямокутника, будуть
асимптотами гіперболи.
.
Прямі, що проходять через протилежні
вершини цього прямокутника, будуть
асимптотами гіперболи.
Ексцентриситет
гіперболи.
Відношення
![]() відстані між фокусами до довжини дійсної
осі називаютьексцентриситетом
гіперболи
і
позначають
відстані між фокусами до довжини дійсної
осі називаютьексцентриситетом
гіперболи
і
позначають
![]() :
:
![]() .
(9.6)
.
(9.6)
Так як
![]() ,
то
,
то![]() .
.
Ексцентриситет
характеризує форму гіперболи. Дійсно,
підставивши в формулу (9.6)
![]() ,
отримаємо
,
отримаємо
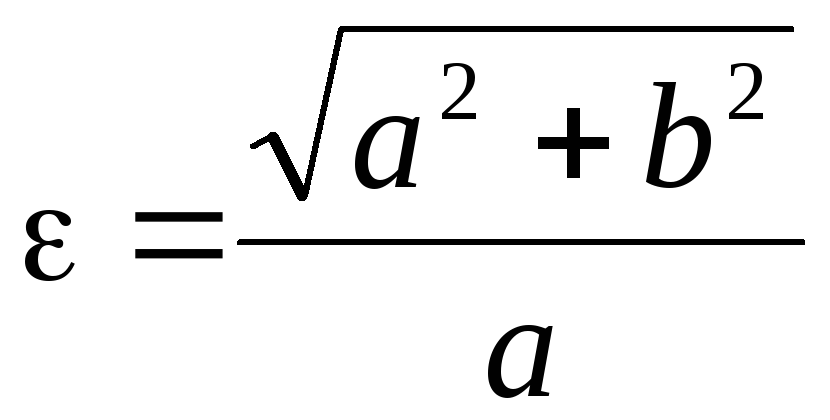 або
або
![]() .
.
Звідси
видно, що чим менше
![]() ,
тим менше відношення
,
тим менше відношення![]() і тим менші кути між асимптотами, в яких
розташована гіпербола.
і тим менші кути між асимптотами, в яких
розташована гіпербола.
Якщо
гіпербола задана рівнянням
![]() ,
то ексцентриситет знаходимо за формулою
,
то ексцентриситет знаходимо за формулою![]() .
.
Приклад
9.3. Скласти
канонічне рівняння гіперболи, фокуси
якої лежать на осі
![]() ,
якщо відстань між фокусами рівна 30, а
дійсна вісь рівна 16.
,
якщо відстань між фокусами рівна 30, а
дійсна вісь рівна 16.
Розв’язок.
Щоб скласти рівняння гіперболи, треба
знайти
![]() і
і![]() .
За умовою
.
За умовою![]() або
або![]() і
і![]() або
або![]() .
Із співвідношення
.
Із співвідношення![]() ,
отримаємо
,
отримаємо![]() .
Таким чином, шукане рівняння матиме
вигляд
.
Таким чином, шукане рівняння матиме
вигляд
![]() .
.
Приклад
9.4. Скласти
канонічне рівняння гіперболи, фокуси
якої лежать на осі
![]() ,
якщо уявна вісь рівна 10, а ексцентриситет
рівний
,
якщо уявна вісь рівна 10, а ексцентриситет
рівний![]() .
Знайти її асимптоти.
.
Знайти її асимптоти.
Розв’язок.
Так
як за умовою
![]() і
і![]() ,
то
,
то![]() і
і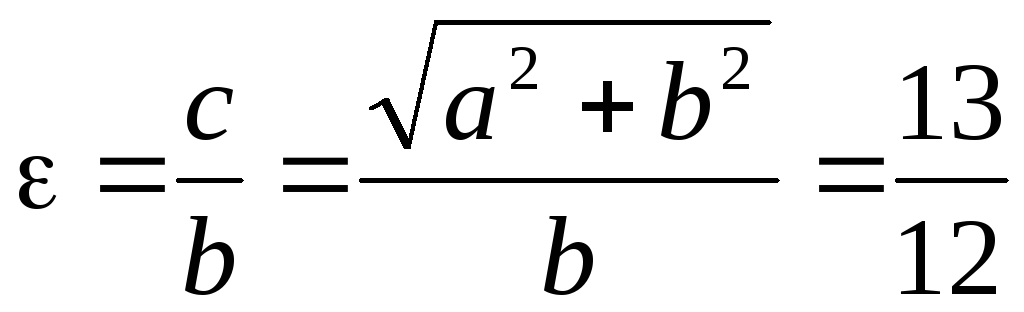 .
Отримаємо:
.
Отримаємо: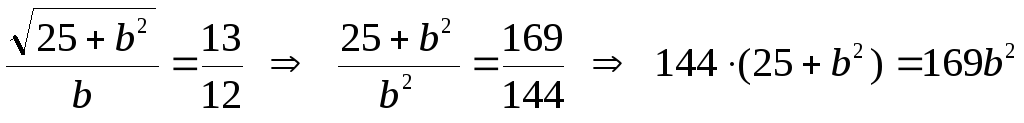 .
Звідки
.
Звідки![]() або
або![]() .
.
Отже, шукане рівняння гіперболи матиме вигляд
![]() ,
,
а рівняння асимптот –
![]() .
.
