Как модуль , так и аргумент комплексного сопротивления контура :

Z=Ze ^{j }

зависят от соотношения индуктивного и емкостного сопротивлений :

Z=;  arctg.

Поэтому определяемая ими по закону Ома амплитуда и начальная фаза тока:

; _ = _u-

также определяется соотношением X_LиX_C . Проиллюстрируем наши рассуждения с помощью векторных диаграмм, рис. 1.14.

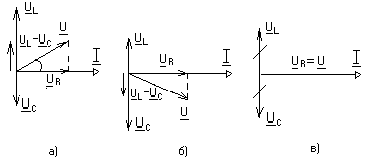
Рис. 1.14.

Здесь возможны три случая:1. X_L>X_C , и, следовательно,U_L>U_C(рис. 1.14. а.).Комплексное сопротивление цепи носит активно-индуктивный

характер. Результирующее напряжение контура опережает ток по фазе

на угол .

2. X_L<X_C , и, следовательно,U_L<U_C(рис. 1.14. б.).

Комплексное сопротивление цепи носит активно-емкостный характер. Результирующее напряжение контура отстает от тока по фазе на угол .

3. X_L=X_C, иU_L=U_C(рис. 1.14. в.).

Комплексное сопротивление цепи носит чисто активный характер. Напряжения на реактивных элементах полностью компенсируют друг друга. Результирующее напряжение равно напряжению на активном элементе и совпадает по фазе с током. Этот случай называется резонансом напряжений и подробно рассматривается в следующей главе.

1.10. Параллельное включение резистивного элемента, идеальной катушки индуктивности и конденсатора в цепь синусоидального тока

При параллельном включении резистора, идеальной индуктивности и конденсатора (рис. 1.15.) входное напряжение цепи является общим, токи в ветвях определяются законом Ома, а ток в неразветвленной части - первым законом Кирхгофа: I=I_R+I_L+I_C или

I=UG-Uj B_L+Uj B_C=U(G +j(B_C- B_L ))= YU.

Рис. 1.15.

Реактивная составляющая комплексной проводимости схемы :

Y= G +j (B_C- B_L )

равна разности проводимостей емкостного и индуктивного элементов и может принимать положительные или отрицательные знаки или обращаться в нуль. Это следствие того, что токи в емкости и индуктивности находятся в противофазе. При равенстве индуктивной и емкостной проводимостей эти токи полностью компенсируют друг друга. При этом в LC контуре циркулирует общий ток, не выходя за его пределы, а ток источника замыкается только через активную проводимость. В результате общий ток в цепи и напряжение на зажимах совпадают по фазе, и получаем режим резонанса токов. Этот режим подробно рассмотрен в следующей главе.

1.11. Смешанное соединение элементов. Разветвленные цепи

Смешанное соединение представляет собой сочетание последовательных и параллельных участков цепи с активными и реактивными элементами. При наличии одного источника анализ данного класса цепей проще всего проводить методом преобразования, используя комплексный способ. Продемонстрируем это на примере цепи, изображенной на рис. 1.16.

Пусть заданы сопротивления всех элементов схемы и напряжение uна ее входе. Требуется определить токи во всех ветвях.

Рис. 1.16.

Для расчета комплексным способом перейдем к комплексной схеме замещения (рис. 1.17.),

Рис. 1.17.

где Z₁ = R₁ +j L₁ ;

Z₂ = R₂ +j L₂ ;

Z₃ = R₃ .

Заменим параллельно соединенные Z₂иZ₃ одним эквивалентным:

.

После этого преобразования схема состоит из двух последовательно соединенных сопротивлений Z₁ иZ₂₃. Полное комплексное сопротивление цепи :Z= Z₁ + Z₂₃.

Ток в неразветвленной части цепи: I=.

Напряжение на параллельно соединенных сопротивлениях:

U₁₂= Z₁₂ I₁ .

Tоки в параллельных ветвях: I₂= I₃=.

В случае разветвленной цепи сложной конфигурации с несколькими источниками анализ проводится по уравнениям, составленным по законам Кирхгофа. Выбор наиболее рационального метода расчета разветвленной цепи синусоидального тока основан на учете особенностей схемы, поставленной задачи и ничем не отличается от аналогичного выбора для цепей постоянного тока.

Рассмотрим на примере особенности преобразования соединения элементов треугольником в соединения звездой.

Пусть необходимо преобразовать часть разветвленной цепи, соединенной треугольником в звезду (рис. 1.18. а).

Рис. 1.18.

Дано: R=X_L= 1 Ом; X_C= 3 Ом.

Решение: Определяем комплексные сопротивления ветвей треугольника.

Z₁₂ = Z₁₃ = R+j X_L= 1+ j 1; Z₂₃= -jXc = -j3.

По формулам преобразования находим комплексные значения сопротивлений эквивалентной звезды.

Z₁=

.

.

.

П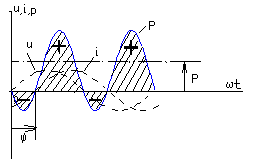ереходя к активным и реактивным сопротивлениям, получим:

R₁ =- 0.4 Ом ; X_L1 = 0.8 Ом ; R₂ = R₃ =2.25 Ом ;

X_C2 = X_C3 = 0.6 Ом .

Эквивалентная схема представлена на рис. 1.18. б. Как видно, активное сопротивление одной из ветвей звезды получилось отрицательным. Это сопротивление, разумеется, имеет только расчетный смысл, т.е. цепь не может быть реализована из пассивных элементов. Активная мощность отрицательного сопротивления также отрицательна, следовательно, электромагнитная энергия в нем не поглощается, а генерируется. Суммарная активная мощность во всех ветвях эквивалентной звезды, конечно же, не отрицательна и равна активной мощности в исходном треугольнике. Примеры численного расчета цепей синусоидального тока комплексным способом с использованием МУП и МКТ в пакете MathCAD представлены в Приложении, файлы: mup.mcd и mkt.mcd.