Задание на срс. Проработать следующие вопросы и задания к сдаче отчета

1. Какие деформации являются элементарными? Как можно классифицировать деформации сгиба и кручения?

2. Ознакомьтесь с понятиями: упругие, неупругие, пластические, остаточные деформации, предел упругости, область текучести, предел прочности.

3. Что такое упругий гистерезис?

4. В чем состоит упрощение реальной ситуации, предлагаемое моделью абсолютно упругого тела?

5. Сформулируйте закон Гука.

6. Дайте определения модуля Юнга, коэффициента Пуассона, модуля сдвига.

7. Почему в качестве величин, характеризующих упругие свойства материалов выбирают пару: модуль Юнга  коэффициент Пуассона, а не пару: модуль Юнга  модуль сдвига?

8. *Получите соотношения (4) и (5).

9. *Рассчитайте работу, которую необходимо затратить на однородное растяжение (сжатие) стержня длиной l и площадью поперечного сечения S на величину l для двух случаев: 1. внешняя сила в каждый момент времени чуть-чуть превосходит силу упругости; 2. внешняя сила все время равна силе упругости деформированного на l стержня. Объясните разницу.

10. *Модуль Юнга можно определить (см. формулы (1) и (2)) как силу, приходящуюся на единицу площади сечения образца, перпендикулярного силе, которая вызывает удлинение образца вдвое. Какие дополнительные оговорки требуется внести в это определение с учетом ответа на предыдущий вопрос

11. Воспроизведите самостоятельно вывод рабочей формулы (6).

12. Выведите формулу для расчета относительной и абсолютной ошибок в определении модуля сдвига и модуля кручения.

Лабораторная работа № 1.6 б определение модуля юнга по изгибу балки

Приборы и принадлежности: линейка, индикатор, штангенциркуль, набор гирь, балки, опоры.

Теория метода

1. Измерение модуля Юнга из изгиба

Изгиб классифицируется как неоднородное растяжение-сжатие. Получим формулу, связывающую параметры изгиба и модуль Юнга.

Рассмотрим изгиб бруса (балки) произвольного сечения, постоянного по всей длине балки. Пусть до деформации брус имел прямолинейную форму (рис. 3). Мысленно проведя нормальные к оси бруса сечения AB и A'B', вырежем бесконечно малый элемент бруса ABA'B', длину которого обозначим через l₀.

Ввиду малости последней можно считать, что в результате изгиба отрезки AA', BB', NN' и все отрезки параллельные им перейдут в дуги окружности с центром на некоторой оси O, перпендикулярной плоскости рисунка (см. рис. 3). Эта ось называется осью изгиба.Наружные волокна, лежащие выше линии NN', при изгибе удлиняются, волокна, лежащие ниже линии NN',  укорачиваются. Длина отрезка NN' остается неизменной. Линия NN' называется нейтральной линией.

Рис.3

Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной плоскости рисунка, называется нейтральным сечением. Пусть R  радиус кривизны нейтрального сечения (R  |NO|). Тогда l₀  R. Рассмотрим волокно бруса, находящееся на расстоянии  от нейтрального сечения. (0, если волокно выше нейтрального слоя, 0 , если  ниже.) Пусть брус не слишком толст, так что R. Тогда длина рассматриваемого волокна равна l   (R  ), а его удлинение l  l  l₀  . Такое удлинение сообщается нормальной к AB силой, величина которой в расчете на единицу площади сечения AB равна:

. (11)

Будем считать, что мы имеем дело только с деформацией изгиба, т.е. сумма сжимающих и растягивающих сил, приложенных сечению AB равна нулю: , где dS - элемент площади рассматриваемого поперечного сечения бруса, интегрирование ведется по всему этому сечению. С учетом выражения (11) . Отсюда ясно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса (например, AB). Из следует, что момент сил M_, действующих на сечение AB, не зависит от того, относительно какой оси он берется. Для вычисления M_ проще всего взять ось, перпендикулярную плоскости рисунка и проходящую через точку N.

Очевидно, , (12)

или , (13)

где введено обозначение

. (14)

Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, I, определяемый выражением (14), имеет размерность четвертой степени длины.

Для бруса с поперечным сечением в виде прямоугольника с шириной a и высотой (AB) b легко получить

. (15)

Направим ось X вдоль нейтральной линии недеформированного бруса, ось Y  перпендикулярно X в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y  y(x). По известной из математического анализа формуле

.

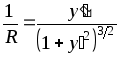Если изгиб мал (y'), то квадратом производной можно пренебречь.

Тогда M_  EIy". (16)

Рассмотрим теперь балку, лежащую на двух опорах (см. рис. 4). Расстояние между опорами равно L. Пусть на балку действует вертикальная сила F. Вследствие симметрии сила F равномерно распределится между опорами. Расстояние между точками О и О' (положениями центра масс до и после изгиба) называется стрелой прогиба. Обозначим ее через z. Поместим начало координат в точку A, направим ось X вправо, а Y  вниз. Отсечем мысленно часть балки, проведя нормальное сечение через произвольную точку С(x) (с координатой x L/2). Справа на отсеченную часть балки будет действовать сила F/2, направленная вниз. Момент внешних сил, действующих на отсеченную часть, будет M = (F/2)x. Условие равновесия моментов принимает вид

. (17)

Знак минус в правой части обусловлен выбором системы координат: функция y(x), описывающая положение нейтральной линии, замедленно растет при x < L/2. Интегрируя уравнение (17) с учетом того, что y'(L/2) = 0 и y(0) = 0, найдем

. (18)

Тогда с учетом (15) получим стрелу прогиба для балки прямоугольного сечения

. (19)

Из выражения (19) легко получить рабочую формулу:

, (20)

где m  масса гири, g  ускорение свободного падения.