Конспект лекций Дин метеорология_2003

Іншою масовою (зовнішньою) силою є сила Коріоліса, яка діє на частки повітря, що рухаються відносно Землі. Сила Коріоліса виникає в результаті переносного обертального руху Землі навколо своєї осі й одночасного руху часток щодо земної поверхні. Як видно з рис.1.15, внас-

Рис. 1.15 - Дія сили Коріоліса на повітряні частки, що рухаються в атмосфері Землі [10]

Позначення: A, At і B, Bt - положення точок земної поверхні А і В у моменти часу t=0 і t=tk; C, Ct - положення частинки, що рухається, у початковий і кінцевий моменти часу; uA ,uB ; - швидкості переносного руху точок земної поверхні А i В, uC ; -

початкова складова абсолютної швидкості частинки, яка дорівнювала швидкості переносного руху вихідної точки А

лідок добового обертання Землі напрямок повітряних течій стосовно земної поверхні змінюється. Він визначається різницею абсолютних величин лінійної швидкості обертального руху різних точок земної поверхні, над якими проходять частинки повітря. Лінійна швидкість обертання точок земної поверхні, яка спрямована із заходу на схід, зменшується від екватора до полюса, де перетворюється в нуль. Частинка повітря, зберігаючи по інерції первісну складову швидкості руху разом із Землею до сходу, при переміщенні з півдня на північ відхиляється на схід від меридіана, на якому вона була в початковий момент часу, а при переміщенні з півночі на південь вона буде відставати від більш південних точок даного меридіана і відхилятися до заходу. За рахунок різниці

31

лінійних швидкостей переносного обертального руху точок земної поверхні, повітряні течії в північній півкулі відхиляються вправо, а в південній - уліво. Таким чином, сила Кориолиса змінює напрямок повітряних течій, не змінюючи абсолютних значень швидкості, і не

виконує ніякої роботи, ( A = (FS ) = FS cos α, α − кут між вектором сили

і напрямком руху дорівнює 90°).

Таким чином, величина сили Коріоліса залежить від кутової

швидкості обертання Землі і відносної швидкості руху частинок повітря (швидкості вітру):

FG	= −2[ωGvG]= 2[vGωG] .	(1.39)
k
Щоб знайти складові сили Коріоліса на осі координат, (для простоти

будемо розглядати декартову систему координат), скористаємося
матричним представленням векторного добутку:
			i		Gj		kG
FG	=− 2[ωGvG]=− 2				ω		ω			=
		ω
k				x		y		z		(1.40)
			u		v		w

= −2[iG(ω y w−ωz v)+Gj(ωz u−ωx w)+ kG(ωx v−ω yu)].

Якщо далі прийняти, що рухома система координат розташована на поверхні Землі і що осі спрямовані на схід, північ і вертикально вгору, то проекції кутової швидкості обертання Землі будуть відповідно дорівнювати: ωx =0, ωy =ωcosϕ, ωz =ω sinϕ , а складові сили Коріоліса:

Fkx =− 2ω( wcosϕ−v sinϕ ), Fky =− 2ωu sinϕ, Fkz =2ωu cosϕ .

1.2.3 Поверхневі сили

Поверхневими силами називають сили, що прикладені до елемента рідини (газу) з боку прилеглих до нього інших частинок або шарів. Ці сили мають таку назву тому, що вони діють тільки на поверхню елемента (частинки). Величина поверхневих сил пропорційна площі цієї поверхні; тому вони розраховуються на одиницю площі, на яку вони впливають, і

називаються напруженнями.

Розглянемо фізичну картину дії поверхневих сил на прикладі плоскопарарельного руху. З досвіду відомо, що кожне, як завгодно мале зусилля, прикладене до частинок рідини або газу, викликає зміщення частинок одна від одної. Однак, ці зусилля супроводжуються виникненням деяких сил, що перешкоджають цьому зрушенню. Ці сили додаються до кожного шару і спрямовані протилежно напрямку зсуву. Властивість рідини або газів чинити опір зусиллям, що зрушують, називається внутрішнім тертям або в'язкістю, а відповідні цьому опору сили називають силами в'язкості.

32

Сутність цього процесу являє обмін молекулами між шарами. З нижнього шару у верхній надходять молекули в середньому з меншою кількістю руху, а на їхнє місце приходять більш швидкі молекули. Молекулярний обмін кількістю руху обумовлює в′язку взаємодію між шарами. Плавна зміна швидкості є прямим наслідком дії сил в'язкості, які згладжують розходження у швидкостях суміжних шарів. Рідке середовище, у якого сили в'язкості відсутні, називається ідеальною рідиною. І навпаки, рідина, у якій не можна зневажити силами в'язкості, називається в′язкою рідиною. Прикладами рідин з малою в'язкістю є спирт, вода, повітря, а з великою в'язкістю - смола, нафта, гліцерін, тощо. В'язкість, як відомо, залежить від температури.

Основна відмінність масових сил від поверхневих полягає в тому, що для перших у кожній точці середовища можна однозначно вказати напрямок дії масової сили. Поверхневі сили в одній і тій же точці мають нескінченну безліч напрямків, тому що через дану точку можна провести безліч площин. Таким чином, хоча поверхневі сили характеризують силову взаємодію між різними частками, їх неможливо представити за допомогою одного вектора. ЗвідсиG випливає очевидна задача: спробувати виразити дію поверхневих сил Pn на довільну площадку з нормаллю nG мінімальним

числом незалежних векторів. Щоб вирішити її, розглянемо наступні поняття і розуміння.

Нехай через довільну точку М проведена довільна площадка δσ з нормаллю n, для якої розрізняють тильну і лицеву частини (рис.1.16).

Рис. 1.16 - Дія поверхневих сил з лицевої та тильної частин [5]

Прийнято угоду, відповідно до якої лицевою вважається частина площадки, звернена до кінця вектора нормалі. Подумки відкинемо частину рідини зGбоку нормалі (з лицевої частини) і замінимо її дію поверхневою силою Pn δσ . Аналогічно, якщо відкинути частину рідини з тильної

33

сторони, то дія поверхневої сили з тильної сторони відповідно до третього закону Н′ютона буде дорівнювати - Pn δσ . Отже, знак поверхневої сили

залежить від того, з якої сторони площадки вона діє.

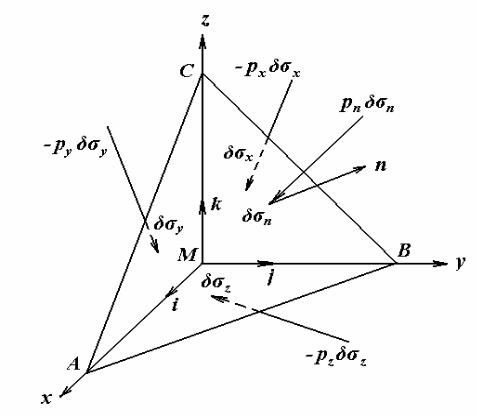
Розглянемо далі елементарний тетраедр такий, що його вершина збігається з початком координат, основа у вигляді трикутника площею δσn перетинає координатні площини, а грані збігаються з координатними

площинами (рис. 1.17), тобто являють собою проекції основи тетраедра на
відповідні координатні площини δσx = δσn cos(n, x), δσy = δσn cos(nG, y) і
δσz = δσn cos(nG, z) . Відповідно поверхневі сили, прикладені до кожної з
граней, визначаються як	Pn δσ n ,− Px δσ x ,− Py δσ y і − PGz δσz , де
PGx , PGy , PGz - вектори напружень, які прикладені до лицевих сторін площадок
δσ x ,δσ y ,δσz . Знак "мінус"	вказує, що зовнішні сторони площадок при

прийнятому напрямку ортів координатних осей виявляються тильними. Розглянемо баланс усіх сил, що діють на частки цього нескінченно

малого тетраедра загальною масою δm . З урахуванням того, що даний тетраедр має нескінченно малі лінійні розміри, усі доданки, які містять масу, пропорційну об′єму, можуть бути відкинуті як нескінченно малі третього порядку величини у порівнянні з іншими доданками, що містять як співмножники елементарні площадки, бо вони є нескінченно малі

другого порядку малості. Тоді будемо мати вираз
pGn δσn =pGx δσx +pGy δσy +pz δσz ,	(1.41)

який означає, що для того, щоб цілком охарактеризувати поверхневі сили в деякій точці, досить визначити сили, що діють на три взаємно перпендикулярні площадки, які лежать у координатних площинах. Виразимо далі проекції елементарних площадок через напрямні косинуси і спростимо обидві частини рівняння на δσn , отримаємо векторну рівність

pGn =pGx nx +pGy ny +pGz nz . Далі спроектуємо поверхневі сили, прикладені до

цих взаємно перпендикулярних площин, на координатні осі:							G	G
G	G	G	G	G	G
px =i pxx + j p yx +k pzx				, p y =i pxy + j p yy +k pzy	, pz	=i pxz + j p yz +k pzz ,
або	pnx =pxx nx +p yx n y +pzx nz ,
	pny =pxy nx +pyy ny +pzy nz ,							(1.42)
	pnz =pxz nx +p yz ny +pzz nz .
	Тут	nx =cos(nG, x), ny =cos(n, y), nz =cos(n, z) -				напрямні		косинуси.

Нагадаємо, що перший порядковий індекс позначає вісь, перпендикулярно до якої орієнтована площина, а другий - вісь, на яку спроектовано напруження. Так наприклад, pxz позначає проекцію напруження на вісь z,

яке прикладене до площини, перпендикулярній осі х. Величини з

34

однаковимиG G G індексами, що представляють проекції векторів напружень px , p y , pz на нормалі до відповідних площин, називають нормальними

напруженями, а їхні проекції на осі, що лежать у площині площадки, -

дотичними. Система рівнянь (1.42) показує, що проекції на осі координат напружень, які прикладені до будь-якої похилої площадки, виражаються

Рис. 1.17 - Розкладання вектора напружень на складові [5]

лінійно через проекції напружень, прикладених до трьох взаємно перпендикулярних площадок, що лежать у координатних площинах, тобто через дев'ять величин, що утворюють тензор 2-го рангу. Позначимо його

pxx

P= pxypxz

або

P= ( p j,i

pyx	pzx
pyy		(1.42)
	pzy
pyz
	pzz
), i, j = 1,2,3		(1.42')

і будемо називати його тензором напружень. Відповідно, діагональні члени цього тензора є нормальними, а недіагональні - дотичними напруженнями. Даний тензор є симетричним.

Хоча в кожній точці середовища існує безліч векторів напружень, що залежать від вибору площадки в даній точці. Відповідно існує безліч

35

векторів-нормалей, але існує єдиний тензор, який характеризує напруженість середовища в даній точці. Цей зв'язок має вираз

G G	pxx	p yx	pzx
	G	p yy		(1.43)
Fn =nP	= n pxy		pzy .
		p yz
	pxz		pzz

Тензор Р являє собою фізичну величину, що виражає стан рідини або газу (їх напруженість), і не залежить від вибору осей координат і утворює поле.

1.2.4 Формули зв'язку

Розглянемо спочатку два важливих часткових випадка: рідину в спокої та ідеальну рідину, що рухається. В обох випадках сили в'язкості відсутні: у першому випадку через відсутність рухів (нульові швидкості), а в другому відсутністю сил в'язкості. Це означає, що дотичні напруження відсутні, а нормальні, прикладені до трьох взаємно перпендикулярних площадок, довільно орієнтованих у просторі, рівні між собою

pxx = pyy = pzz = −p	(1.44)
де р - гідростатичний тиск, розмірність якого	[p]= н / м2 . Це закон

ізотропіі нормальних напружень точок середовища, що знаходяться в рівновазі, був відкрит Паскалем у XVII столітті. Оскільки дія тиску завжди спрямована по нормалі всередину рідини, тобто протилежно напрямку нормалі до даної поверхні, він береться зі знаком "-". Величина тиску не залежить від орієнтації площадки і від вибору системи координат і є скалярною величиною. Отже, тензор напружень буде мати вигляд

− p 0			0		1 0		0
	0	− p	0					= −pU ,	(1.45)
P =					= −p 0	1 0
	0	0				0
			− p		0		1

де U - одиничний тензор.

Для ідеальної рідини вважається, що на площадки зіткнення об′ємів, що рухаються, діють лише нормальні до них сили тиску. Причому, вони також не залежать від напрямку площадки, до якої прикладені. Тиск в ідеальній рідині, що рухається, називають гідродинамічним.

У реальній атмосфері, при наявності в'язкості повітря, поверхневі сили не збігаються з напрямком нормалі до поверхні і розкладаються на нормальну і дотичну складові, які діють уздовж поверхні і перешкоджають сковзанню окремих шарів і частинок відносно одна одної. У зв'язку з цим нагадаємо, що рух повітряної частинки залежить не тільки від поступального й обертального руху елементарної частинки, але і від її

36

деформації. Можна також стверджувати, що оскільки сили в'язкості, що обумовлюють напруження, перешкоджають сковзанню частинок і шарів повітря між собою, з ними повинні бути пов'язані деформації об′єму повітря, які призводять до зміни відстаней між його частинками.

Найпростішим прикладом лінійного зв'язку між дотичним напруженням і деформацією для плоско паралельного руху є формула

	Н′ютона		∂u
	pzx	= µ		,	(1.46)
			∂z

де µ - динамічний коефіцієнт в'язкості, що має розмірність н/(м2с) і чисельно дорівнює дотичній напруження при одиничній зміні швидкості на одиницю відстані. Цей коефіцієнт не залежить від швидкості і будь-якої комбінації від диференціальних характеристик поля швидкості, а є мало мінливою функцією температури (Т) рідини (газу). Для повітря ця залежність має вид:

µ =1,15T 8 / 9 .	(1.47)
Для характеристики	в'язкості рідини часто використовують

кінематичний коефіцієнт в'язкості ν = µρ , що має розмірність м2/с.

Причому, якщо динамічний коефіцієнт в'язкості характеризує дотичне напруження в'язкості при даному полі швидкості, то кінематичний коефіцієнт в'язкості характеризує прискорення частинок рідини, викликане напруженням сили в'язкості. Він також залежить від температури. Розходження між коефіцієнтами в'язкості для води і повітря пов'язані з відмінністю у густині і великим впливом сил зчеплення. Останні залежать від температури і густини: зі зростанням температури підсилюються коливальні рухи молекул і відповідно убувають сили в'язкості: цей процес значно швидше відбувається у рідини, ніж у повітрі.

Як випливає з порівняння тензорів напружень і деформацій,

скошування прямих кутів викликається дотичними напруженнями поверхневих сил у відповідних площинах, а деформації стискання або розширення - нормальними напруженнями поверхневих сил. У

загальному випадку зв'язок між складовими тензорів напружень і деформацій встановлюється узагальненим законом Н′ютона:

P=aД +bU ,

(1.48)

де a і b скаляри, a=2µ = 2ρν . Перший доданок встановлює лінійний зв'язок між складовими тензорів напружень і деформацій, а другий враховує вплив сили тиску і змін елементарного об′єму при його розтяганні або стисканні. При цьому вводиться гіпотеза про те, що сума нормальних напружень дорівнює потроєному гідродинамічному тиску:

37

( pxx + pyy + pzz ) =−3р,

Варто відзначити, однак, що формулювання гіпотези для виразу нормальних напружень може бути й іншим. Це пов'язано з тим, що не можна строго довести, що скалярна величина p дійсно буде тією величиною, що пов'язана з температурою і густиною в рівнянні стану Менделєєва-Клапейрона, хоча правильність подібної гіпотези виправдовується практикою майже у всіх областях її застосування.

З урахуванням цієї гіпотези знаходимо, що

b = −p −23 ρνdivVG . (1.49)

Тоді складові тензора напружень можуть бути представлені у вигляді:

pxz = pzx =ρν(

∂ u

+

∂ w

),

∂ z

∂ x

pxy = p yx = ρν(

∂ u

+

∂ v

),

(1.50)

∂ y

∂ x

p yz = p yz = ρν(

∂ v

+

∂ w

),

∂ z

∂ y

pxx =− p + 2

ρν(

∂ u

−

1

divVG),

∂ x

3

p yy = −p + 2ρν(

∂ v

−

1

divVG),

(1.51)

∂ y

3

pzz = −p + 2

ρν(

∂ w

−

1

divVG).

∂ z

3

38

2 ОСНОВНІ РІВНЯННЯ ДИНАМІЧНОЇ МЕТЕОРОЛОГІЇ

2.1 Суцільність середовища

Як відомо, атмосфера є сумішшю газів і являє собою систему, яка складається з величезного числа елементарних частинок (молекул у нижній тропосфері, атомів і молекул у верхній атмосфері). Тому виникає питання: чи можна абстрагуватися від дискретної структури атмосфери і розглядати її як суцільне середовище. Якщо прийняти гіпотезу суцільності, то тоді можна ввести ряд макроскопічних величин (швидкість вітру, температуру, густину, тиск) і сформулювати рівняння для опису змін цих величин у просторі і в часі.

Для того, щоб це зробити, треба провести осереднення по елементарному об′єму, розміри якого повинні задовольняти наступним умовам: лінійні розміри об′єму lo повинні бути великі в порівнянні з

довжиною вільного пробігу молекул lm , але бути значно менші в

порівнянні з характерним масштабом явища	L=b / grad b (b –
метеорологічна величина), тобто
lm << l0 << L .	(2.1)

Перша умова виключає флуктуації, пов'язані з молекулярними рухами, а друга - зміни осереднених величин всередині об′єму. Очевидно, що чим більше число частинок входить в елементарний об′єм, тим менший вплив флуктуацій на середню величину. (Внаслідок цього середній вектор швидкості теплового руху практично дорівнює нулю.) З іншого боку, розмір елементарного об′єму, хоча і менший від характерного розміру розглянутого явища, все-таки дозволяє простежити за змінами осереднених величин від одного елементарного об′єму до другого.

Слід зазначити, що вказані розміри залежать від багатьох факторів. Так, довжина вільного пробігу молекул росте з висотою, характерні розміри явища мають широкий діапазон. Якщо прийняти, що розмір елементарного об′єму більше 1 м, то на висотах менш 100 км атмосферу можна вважати за суцільне середовище. Проте для висот більше 100 км атмосферу необхідно вже трактувати як дискретне середовище.

2.2 Загальне формулювання рівняння балансу

При вивченні динаміки атмосферних процесів становлять інтерес поля тиску, температури, швидкості вітру та інших величин. Для дослідження їх змін необхідно сформулювати відповідні рівняння. Вони ґрунтуються на трьох основних законах збереження: маси, імпульсу й енергії. З їхньою допомогою отримують відповідно рівняння нерозривності, дифузії різних

39

компонентів, рівняння руху і припливу тепла. При їх виведенні зручно керуватися міркуваннями, що використовують при формулюванні загального рівняння балансу.

Розглянемо масу повітря, що рухається, із густиною ρ . Нехай a деяка

питома скалярна величина, тобто віднесена до одиниці маси, а в одиниці об'єму буде міститься кількість субстанції ρa . За одиницю часу її зміни

будуть ∂ρa / ∂t . В елементарному об′ємі - ( ∂ρa / ∂t )dτ, а у всьому об′ємі -

∫∫∫(∂ρa / ∂t)dτ . Ці зміни можуть бути обумовлені припливом (відтоком)

τ

розглянутої субстанції через поверхню об′єму ∫∫ρ a Vn dS і наявністю

S

джерел/стоків ∫∫∫I dτ. Тут S - поверхня, що стягує даний об′єм, I -

τ

потужність джерел (стоків), тобто кількість субстанції, що виникає (зникає) за одиницю часу. ρ a Vn - потік субстанції через одиничну

поверхню, Vn - нормальна складова макроскопічної швидкості руху

субстанції, що розглядається. Тоді загальне рівняння балансу може бути записано у вигляді:

∫∫∫(∂ ρ a / ∂t)dτ = - ∫∫ρ a Vn dS + ∫∫∫I dτ.			(2.2)
τ	S	τ

Звернемо увагу на знак «мінус» перед першим доданком у правій частині. Він пов'язаний з тим, що потік субстанції через поверхню приймається позитивним, якщо він збігається з напрямком нормалі до неї. Отже, якщо відбувається відтік, то потік позитивний, і, таким чином, відбувається зменшення субстанції в об′ємі τ. І, навпаки, при припливі - потік негативний, а зміна в часі - позитивна.

Формула Остроградського-Гаусса дозволяє замінити інтеграл по замкненій поверхні потрійним інтегралом по області, обмеженою цією

поверхнею, тобто ∫∫ρ a Vn dS=∫∫∫div(ρaV )dτ.

S	τ
Тоді
∫∫∫(∂ρa / ∂t)dτ =−∫∫∫div(ρaV )dτ + ∫∫∫I dτ
τ	τ	τ
або
∫∫∫(∂ρa / ∂t+ divρaVG −I )dτ = 0.		(2.3)

τ

40