книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Глава 21. Нелинейные электрические и магнитные цепи при периодических процессах

403

уравнениях комплексные сопротивления нелинейных инерционных элементов, т. е. модули и аргументы этих сопротивлений, будут функциями действующих токов в этих элементах. Следовательно, алгебраические уравнения, записанные в комплексной форме согласно законам Кирхгофа, являются теперь нелинейными. Трудность решения их заключается в том, что в общем случае от действующего тока в нелинейном элементе могут зависеть и модуль, и аргумент комплексного сопротивления элемента. Но даже если изменяется только модуль этого сопротивления, расчет остается сложным, так как это изменение ведет к перераспределению амплитуд и изменению фаз токов во всех ветвях цепи.

Можно рекомендовать при синусоидальном приложенном напряжении следующий метод последовательных приближений. Задаемся некоторыми вероятными значениями комплексных сопротивлений Z s zs ej!s нелинейных элементов и, считая их постоянными, производим расчет цепей. Определив действующие токи в нелинейных элементах, проверяем соответствие заданных параметров элементов значениям этих параметров, полученных из действительных характеристик нелинейных элементов при найденных значениях токов. При несовпадении значений параметров вносим поправки в них и производим повторный расчет. Этот расчет следует выполнять до тех пор, пока принятые для рас- чета значения параметров не будут достаточно близки к их значениям, полученным из характеристик.

Инерционными элементами с сопротивлениями, как было указано в § 19.4, являются, например, такие, которые обладают большой тепловой инерцией (например, лампы накаливания). Примером инерционного индуктивного элемента может служить электромеханический элемент, который рассмотрим в следующем параграфе.

Синусоидальные установившиеся режимы в сложных электроэнергетиче- ских системах в некоторых случаях также могут быть описаны системами нелинейных алгебраических уравнений. Такая возможность возникает, когда оказываются заданными не ЭДС и параметры линий и нагрузок, а значения потребляемых и генерируемых мощностей. При условии задания потребляемой мощности ток и напряжение оказываются взаимосвязанными через нелинейное сопротивление (или проводимость). Действительно, если

								*		*	const,
						p ui const è S				IU
	p						*
							S	*
òî i			f (u)	èëè	I			f (U ).
							*

u	U

В сложных электроэнергетических системах с точки зрения эксплуатационных характеристик и из-за особенностей соединений генераторов и потребителей наиболее целесообразно в качестве искомых величин выбирать напряжения в узлах системы. С учетом этого для расчета таких систем наиболее распространен метод узловых напряжений. Относительно узловых напряжений можно записать

A	t		t	*	1 *
		YAU A		(1U )	S.
Здесь Y — матрица комплексных узловых проводимостей; A — матрица со-
					*	— матри-
единений; U — матрица-столбец узловых комплексных напряжений; S

Ðèñ. 21.1

404 Часть 3. Теория нелинейных электрических и магнитных цепей

ца-столбец заданных комплексных мощностей источников и приемников. Это матричное уравнение по указанным выше причинам представляет собой систему нелинейных алгебраических уравнений относительно комплексных узловых напряжений. Разделив вещественные и мнимые составляющие, можно записать

t		t	*	1	*	Ô1(U1,U2 ) jÔ2 (U1,U2 ) 0
A YAU A			(1U )		S

èëè

Ô1(U1,U2 ) 0 è Ô2 (U1,U2 ) 0.

Последняя система уравнений, написанная для вещественных матриц U1 è U2, может быть решена изложенными во второй главе методами простых итераций или Ньютона. Разумеется, методы расчета сложных электрических систем не ограничиваются приведенными выше. В зависимости от поставленной задачи и характера заданных исходных данных могут быть сформированы различные системы уравнений. Однако для всех этих подходов остается общим то, что в конечном итоге формируется система нелинейных алгебраических уравнений. Приведенные в качестве примера методы решения таких систем уравнений (метод простой итерации и метод Ньютона) являются основой для разработки других, более эффективных методов расчета сложных нелинейных цепей переменного тока в установившихся режимах.

21.2. Процессы в цепи с индуктивным инерционным электромеханическим элементом

Рассмотрим электромагнит, питаемый синусоидальным действующим током I; между его полюсами может вдоль направляющих вертикально перемещаться массивный ферромагнитный якорь (рис. 21.1). Положение якоря определим координатой x, отсчитываемой от некоторого начального положения (от упора якоря). К якорю приложены сила тяжести G, направленная вниз, и электромагнитная сила F, втягивающая якорь в пространство между полюсами электромагнита

и направленная вверх.

Мгновенная электромагнитная сила f, согласно изложенному в § 2.4, т. I, имеет выражение

f i2 ΗL . 2 Ηx

Если осуществить зависимость L(x) â âèäå L ax + L0, òî ΗL/Ηx à const. При достаточно массивном якоре вследствие инерции положение его остается практически неизменным в течение периода изменения тока. Поэтому среднее за период значение электромагнитной силы F равно

		1	T	a		1	T	a
	F		f dt				i2 dt		I 2 .
		T		2		T		2
			0				0

Эта сила уравновешивается силой тяжести G, и, следовательно,

G 2a I 2 .

Глава 21. Нелинейные электрические и магнитные цепи при периодических процессах

405

Òàê êàê G const, òî è I const I0, т. е. такое устройство осуществляет стабилизацию действующего тока.

Зависимость L ax + L0 имела бы место, если бы зазор − между якорем и полюсами оставался неизменным, все линии магнитного потока проходили через зазор и можно было бы пренебречь магнитными сопротивлениями якоря и сердечника. При этом

L

<L

wΜ

w2 Μ

w2

w2

,

2− (

i

i

iw

Rì

0 s)

где сечение, сквозь которое проходит магнитный поток в зазоре, s bl b(x + l0).

Таким образом, L w2 0 b (x l0 ) ax L0 . При этих идеальных условиях ин- 2−

дуктивность остается постоянной, равной L0, до тех пор, пока якорь лежит на упоре, т. е. пока I < I0 è F < G. При этом с увеличением напряжения UL на катушке ток растет пропорционально ему: UL I L0, что соответствует начальной прямолинейной ветви 0c характеристики катушки (рис. 21.2). Как только ток достигнет значения I0, будет иметь место равенство F G и якорь окажется во взвешенном состоянии. Если увеличить напряжение выше значенияU L0 , то при том же нижнем положении якоря на упоре увеличится ток выше значения I0, ñèëà F будет больше G и якорь поднимется. Он будет подниматься до тех пор, пока вследствие возрастания индуктивности L ток не упадет вновь до значе- ния I0, при котором будет иметь место равенство F G. Каждому значению напряжения UL соответствует свое значение индуктивности L, т. е. определенное положение якоря. Таким образом, характеристика катушки UL(I), испытав излом в точке c, дальше идет в виде вертикальной прямой, и в пределах этой прямой данное устройство работает как стабилизатор тока. Если этот нелинейный элемент включить последовательно с приемником, имеющим сопротивление Zïð (рис. 21.3), то в известных пределах изменения приложенного напряжения U на зажимах цепи ток в приемнике окажется неизменным. Реальная характеристика несколько отличается от идеальной и представлена на рис. 21.4.

Ðèñ. 21.2

Ðèñ. 21.3

Ðèñ. 21.4

В соответствии с изложенным в предыдущем параграфе расчет режима в цепи при заданном напряженииU ведем методом последовательных приближений. Задаемся некоторым значением L1 индуктивности L нелинейного элемента и вы- числяем ток, который был бы в цепи при этом значении L1:

406 Часть 3. Теория нелинейных электрических и магнитных цепей

I1 j L1U Z ïð .

При этом действующее напряжение на катушке было бы равно U L1 I1 L1. Этим значениямU L1 è I1 соответствует точка 1 на рис. 21.4. Если эта точка не легла на характеристику катушки, то индуктивность L1 была выбрана неправильно. Задаваясь рядом значений индуктивности L, получим точки 2, 3, 4. Проводя че- рез эти точки кривую, получим на пересечении ее с характеристикой катушки точку d, определяющую искомый режим.

21.3. Особенности периодических процессов в цепях с безынерционными нелинейными элементами. Метод эквивалентных синусоид

Если хотя бы один нелинейный элемент в цепи является безынерционным, то периодические токи и напряжения в цепи будут содержать высшие гармоники, даже если приложенное к зажимам цепи напряжение синусоидальное. Пусть характеристика нелинейного элемента, изображенная на рис. 21.5, à, выражается уравнением i au 3. При синусоидальном изменении напряжения ток будет

iaU m3 sin3 t 34 aU m3 sin t 14 aU m3 sin t,

ò.е. он содержит третью гармонику.

Ðèñ. 21.5

Íà ðèñ. 21.5, á изображены во времени кривые тока и напряжения. Кривую тока i(t) можно было бы построить графически по точкам, пользуясь характеристикой u(i). Уже из этого примера видно, что ток и напряжение на безынерционном элементе не могут быть одновременно синусоидальными. Для сложной цепи расчет является весьма сложным, так как использование комплексной формы записи и векторных диаграмм оказывается невозможным, и расчет необходимо вести для мгновенных величин, причем из-за нелинейности цепи неприменим и метод наложения.

В тех случаях, когда вопрос о форме кривых токов и напряжений нас непосредственно не интересует, можно воспользоваться приближенным методом, основанным на замене действительных несинусоидальных кривых тока и напряжения эквивалентными им синусоидами. Соответственно, такой метод можно назвать м е т о д о м э к в и в а л е н т н ы х с и н у с о и д.

Смысл ведения этого метода заключается в возможности записи уравнений в комплексной форме, а также в построении векторных диаграмм, хотя комплекс-

Глава 21. Нелинейные электрические и магнитные цепи при периодических процессах

407

ные сопротивления остаются зависящими от тока, а следовательно, алгебраиче- ские уравнения, записанные в комплексной форме, остаются нелинейными.

Выбор эквивалентных синусоид тока и напряжения, т. е. их амплитуд и на- чальных фаз, может быть осуществлен тем или иным способом в зависимости от поставленной задачи. Интересуясь энергетической стороной процесса, этот выбор целесообразно осуществить так, чтобы активная мощность в цепи или в той или иной части цепи оставалась без изменения. Например, если мы желаем, чтобы активная мощность на нелинейном элементе, характеристика которого приведена на рис. 21.5, à, при синусоидальном напряжении на этом элементе осталась неизменной после замены несинусоидальной кривой тока эквивалентной ей синусоидой, то в этих условиях эквивалентной синусоидой должна быть первая гармоника тока, так как при этом имеем (см. § 8.4, т. 1)

P I1U1 cos !1 I 2U 2 cos !2 I 3U 3 cos !3 U1I1 UI1.

Действительно, в данном случае U2 U3 ... 0, U1 U è cos !. .

Иногда может оказаться целесообразным выбор эквивалентной синусоиды тока или напряжения так, чтобы сохранялось их действующее значение. Например, это целесообразно, когда последовательно включены линейный резистор r с нелинейной индуктивной катушкой без потерь. В таком случае несинусоидальный ток i(t) в катушке имеет смысл заменить синусоидой, эквивалентной ему по действующему значению, т. е. выбрать амплитуду эквивалентной синусоиды равной

					1		T
	I mý	2	I	2			i2 (t) dt.
						T
							0

Действительно, в этом случае активная мощность в линейном резисторе r, равная I 2r , остается без изменения.

Метод эквивалентных синусоид находит применение при расчете периодиче- ских процессов в нелинейных радиотехнических устройствах, например в ламповых генераторах. При этом в качестве эквивалентной синусоиды применяют первые гармоники тока и напряжения, так как именно на их частоту настраивают резонансные контуры, в которых токи и напряжения в основном и определяются первыми гармониками.

Широкое использование метод эквивалентных синусоид находит при расчете устройств, содержащих ферромагнитные сердечники, например трансформаторов. В связи с этим рассмотрим этот метод более подробно в применении к реактивным катушкам и трансформаторам с ферромагнитными сердечниками.

Подчеркнем еще раз, что по своей сути этот метод является приближенным, но при нем получаем возможность пользоваться комплексной записью уравнений и векторными диаграммами.

21.4. Формы кривых тока, магнитного потока и ЭДС в катушке с ферромагнитным сердечником

Так как катушки с ферромагнитным сердечником находят весьма широкое применение в цепях переменного тока, рассмотрим вопрос о влиянии нелинейной

408 Часть 3. Теория нелинейных электрических и магнитных цепей

зависимости магнитного потока в таких катушках от тока в них на форму кривых тока, потока и ЭДС.

Связь < f(i) определяется петлей гистерезиса (рис. 21.6), если можно пренебречь влиянием вихревых токов, о котором будет сказано позже. Пусть потокосцепление <, а следовательно, и ЭДС в обмотке катушки e –d</dt, а также напряжение u d </dt, ее уравновешивающее, изменяются по синусоидальному закону (рис. 21.6). В таком случае кривая тока в обмотке катушки содержит высшие гармоники, преимущественно третью, пятую и седьмую. Кривую тока нетрудно построить по точкам, как это показано на рис. 21.6. Максимумы тока и потока совпадают, но через нуль кривая тока проходит раньше кривой магнитного потока. Кривая тока имеет заостренную форму. В другом предельном случае, когда ток изменяется по синусоидальному закону, кривая магнитного потока отлична от синусоиды и имеет уплощенную форму (рис. 21.7). Кривые же ЭДС e, равной –d </dt, и напряжения u, равного d </dt, при этом имеют весьма заостренную форму (рис. 21.7). Построение кривой потока по заданной кривой тока и петле гистерезиса нетрудно осуществить по точкам графически. Кривую же напряжения получаем дифференцированием кривой потока.

Ðèñ. 21.6

В общем случае как кривая тока, так и кривая напряжения могут оказаться несинусоидальными.

Ðèñ. 21.7

Обратим внимание на то, что вследствие симметричной формы петли гистерезиса в рассмотренных случаях (рис. 21.6 и 21.7) несинусоидальные кривые тока, потока и напряжения симметричны относительно оси абсцисс и, следовательно, не содержат четных гармоник.

Ðèñ. 21.8

Глава 21. Нелинейные электрические и магнитные цепи при периодических процессах

409

21.5. Потери в сердечниках из ферромагнитного материала

Для правильного выбора эквивалентных синусоид, заменяющих действительные несинусоидальные кривые тока и напряжения в катушках с ферромагнитными сердечниками, необходимо рассмотреть потери энергии в сердечниках при периодическом изменении магнитного потока. Эти потери складываются из потерь на вихревые токи и на гистерезис.

Сердечники большей частью набирают из тонких листов ферромагнитного материала, изолированных друг от друга тонким слоем изоляции с целью уменьшения потерь на вихревые токи.

Вихревые токи, согласно принципу Ленца, направлены таким образом, что созданное ими магнитное поле ослабляет результирующее поле. Это ослабление наиболее резко выражено в середине листа. Поэтому результирующее магнитное поле распределяется неравномерно по сечению листа. Толщину листа для уменьшения потерь выбирают малой; при этом можно пренебречь неравномерностью поля внутри листа, т. е. размагничивающим действием вихревых токов. Подробно этот вопрос будет рассмотрен в четвертой части курса при исследовании переменного электромагнитного поля в проводящей среде. Приняв такое допущение, легко можем получить зависимость потерь на вихревые токи от амплитуды магнитной индукции, частоты и удельной проводимости материала листа.

На рис. 21.8 показана трубка вихревого тока, имеющая сечение l dx и длину, приблизительно равную 2h. Активная проводимость вдоль этой трубки обратна ее активному сопротивлению, поскольку мы пренебрегаем магнитным полем вихревых токов и, следовательно, соответствующим индуктив-

ным сопротивлением. Имеем dgx Ξ l2dxh . Действующая ЭДС,

индуцируемая вдоль трубки, равна

E x 4kô fΜmx 4kô f 2xhÂm ,

ãäå kô — коэффициент формы кривой ЭДС. Следовательно, потери внутри трубки тока равны dPâ E x2 dgx 32hlΞkô2 f 2 Bm2 x 2 dx. Интегрируя от 0 до d/2, получа- ем потери на вихревые токи во всем листе:

	P	4	Ξk2 d 2 f 2 B 2V ,
		3
	â		ô	m

ãäå V hld — объем листа. Таким образом, потери на вихревые токи при принятом допущении пропорциональны квадрату частоты, квадрату амплитуды индукции, квадрату толщины листа и первой степени удельной проводимости.

Для сердечника из проволок круглого сечения с диаметром d, оси которых направлены вдоль линии магнитной индукции, при том же допущении получим вместо коэффициента 4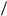3 коэффициент 12. Обобщая полученный результат, можем написать

Pâ Ψ f 2 Bm2V ,

410 Часть 3. Теория нелинейных электрических и магнитных цепей

где коэффициент Ψ зависит от формы сечения элементов, на которые разделен сердечник, геометрических размеров этого сечения, удельной проводимости материала и коэффициента формы kô.

Потери на гистерезис в единице объема вещества за один цикл перемагни- чивания, как было указано в § 19.12, могут быть выражены в видеWã ?Bmn , где коэффициент ? зависит от свойств ферромагнитного вещества. Следовательно, мощность потерь на гистерезис в объеме V, равная потерям энергии в единицу времени, т. е. за f циклов, может быть выражена в виде

Pã ?fBmnV .

В диапазоне амплитуд индукции, с которым обычно имеем дело в электротехнических устройствах, можно принять n 2.

Таким образом, суммарная мощность потерь в сердечнике может быть представлена формулой

Pôåð Pã Pâ ?fBm2V Ψ f 2 Bm2V .

То обстоятельство, что мощность Pã пропорциональна первой степени частоты, а мощность Pâ — квадрату частоты, позволяет экспериментально разделить суммарные потери Pôåð íà Pã è Pâ, произведя два измерения при двух частотах, но при неизменной амплитуде магнитной индукции. С этой целью необходимо в этих двух опытах иметь одинаковое отношение ЭДС к частоте.

21.6. Эквивалентные синусоиды и зависимость между потокосцеплением и током

Заменим несинусоидальный ток в катушке с ферромагнитным сердечником и напряжение на ее зажимах эквивалентными синусоидами. Надлежит выбрать амплитуды Um è Im эквивалентных синусоид и угол сдвига фаз ! между ними. Здесь мы рассматриваем напряжение, уравновешивающее ЭДС, индуцируемую в обмотке катушки переменным магнитным потоком в сердечнике, не учитывая падения напряжения в активном сопротивлении обмотки и индуктивного падения напряжения, опредеëÿемого поòоками рассеяния.

Связь между !, Um 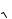2U è Im 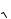2I для эквивалентных синусоид определяется из условия сохранения потерь в сердечнике, т. е. из условия

UI cos ! Pôåð Pã Pâ .

Необходимы еще два условия для определения всех трех величин !ϑ Um 2U è Im 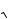2I. Этими условиями могут быть, как было сказано в § 21.3, выбор Um è Im равными амплитудам первых гармоник напряжения и тока или выбор U è I равными действующим несинусоидальным напряжениям и току.

Замена действительных кривых тока эквивалентными синусоидами приводит к тому, что связь < è i выражается уравнением эллипса, площадь которого в соответствующих масштабах равна потерям в сердечнике за один период. В зависимости от выбора амплитуд Um è Im эквивалентных синусоид получим тот или иной эллипс, но все эти эллипсы должны иметь одну и ту же площадь.

При синусоидальном напряжении, соответственно, при синусоидальном потоке в качестве амплитуд Um è <m естественно взять действительные амплитуды

иной вид эллипса.

Глава 21. Нелинейные электрические и магнитные цепи при периодических процессах

411

этих величин. Амплитуду же Im следует выбрать либо равной амплитуде первоé гармоники тока i, либо равной его действующему значению, умноженному на 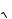2. Соответственно тому или другому выбору амплитуды эквивалентной синусоиды тока получим то или иное значение ! и тот или иной вид эллипса.

При синусоидальном токе естественно выбрать величину Im равной действительной амплитуде тока i. Амплитуду же Um следует выбрать либо равной амплитуде первой гармониêи напряжения u, либо равной его действующему значе- нию, умноженному на 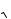2. Амплитуда <m определится из равенства Um <m. Соответственно, получим то или иное значение ! и тот или

На рис. 21.9 и 21.10 сказанное иллюстрируется в предположении, что учитываются только потери на гистерезис. Рис. 21.9 относится к синусоидальным напряжению u и потоку <, а рис. 21.10 — к синусоидальному току i. В этих случаях площадь эллипса равна площади петли гистерезиса. Наличие вихревых токов несколько приближает к эллипсу действительную кривую <(i). Площадь эквивалентного эллипса при этом должна быть взята равной площади

этой действительной кривой, равной в соответ- Ðèñ. 21.9 Ðèñ. 21.10 ствующем масштабе суммарным потерям в сердечнике.

21.7. Уравнение, векторная диаграмма и эквивалентная схема катушки с ферромагнитным сердечником

Рассмотрим процессы в катушке с замкнутым ферромагнитным сердечником, обмотка которой имеет w витков.

Уравнение, описывающее процесс в катушке, имеет вид

u ri ddt< ,

ãäå r — сопротивление обмотки.

Полное потокосцепление представим в виде суммы < <Κ + <0. Величина <0 есть потокосцепление, определяемое линиями магнитной индукции, замыкающимися целиком вдоль сердечника. Следовательно, <0 wΜ0, ãäå Μ0 — поток сквозь сечение сердечника, определяемый этими линиями. <Κ есть потокосцепление, определяемое линиями магнитной индукции, замыкающимися частично или полностью в воздухе.

Разделение величины < на <Κ è <0 имеет тот смысл, что потокосцепление <Κ пропорционально току: <Κ LΚi, так как магнитное сопротивление пути, по которому замыкаются линии потока, практически не зависит от тока и, следовательно, индуктивность LΚ постоянна. Потокосцепление <0 нелинейно связано с током i, так как магнитная проницаемость и, следовательно, магнитное сопротивление сердечника зависят от напряженности магнитного поля. Уравнение катушки теперь можно переписать в виде

Μ0m

412 Часть 3. Теория нелинейных электрических и магнитных цепей

u ri LΚ dtdi w ddtΜ0 ri LΚ dtdi u0 .

Это уравнение нелинейное. Поэтому, даже если приложенное напряжение u синусоидально, ток i будет несинусоидальным. Заменяя несинусоидальные кривые тока и потока эквивалентными синусоидами, можем записать это уравнение в комплексной форме для комплексных амплитуд:

U m rI m j LΚI m j wΜ0m rI m j LΚI m U 0m .

Согласно изложенному в предыдущем параграфе, эквивалентная синусоида тока i отстает от эквивалентной синусоиды напряжения u0 d<0/dt íà óãîë !0 < #/2 вследствие наличия потерь в сердечнике Pôåð Pã + Pâ

U0I cos !0 > 0. Таким образом, эквивалентная синусоида потока <0 отстает от эквивалентной синусоиды тока i íà óãîë

#/2 – !0, так как эквивалентная синусоида потока <0 отстает от эквивалентной синусоиды напряжения u0 íà óãîë #/2.

На рис. 21.11 изображена векторная диаграмма катушки, соответствующая уравнению катушки, записанному в комплексной форме. На диаграмме отложен вектор ЭДС, индуцируемой

в обмотке потоком Μ0, равной e0 –wddtΜ0 .

Òîê I можно разложить на две составляющие: Ið, находящуюся в фазе с потоком, и Ià, находящуюся в квадратуре с потоком.

Ðèñ. 21.11 Величина Ið представляет собой реактивную составляющую тока, а величина Ià — активную составляющую. Соответственно, можем изобразить катушку с помощью эквивалентной схемы, приведенной на рис. 21.12, причем

b

I

ð

I

à

I

U

0

Pôåð

è g

à

.

0

0

U

U

U 2

U 2

Ðèñ. 21.12

0

0

0

0

21.8. Комплексное магнитное сопротивление магнитной цепи

То обстоятельство, что поток Μ0 в ферромагнитном сердечнике катушки отстает по фазе на угол от намагничивающего тока i в обмотке катушки и, следовательно, от МДС iw, можно учесть, введя в закон магнитной цепи

I mw Z ì

к о м п л е к с н о е м а г н и т н о е с о п р о т и в л е н и е сердечника

Z	ì			Z	ì		ej R	ì	jX	ì	.

Выразим комплексное магнитное сопротивление через длину l сердечника, сечение s сердечника и магнитную проницаемость вещества сердечника. Сече- ние s будем считать одинаковым по всей длине сердечника. Получаем