книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Ответы на вопросы, решения упражнений и задач

513

	t		U 0		t			U 0
	á) t < t1: i1(t) Y(t x)				dx, t > t1: i1(t) 1 Y(t x)				dx – U0Y(t – t1) ;
	0		t1		0			t1
	t	U 0			t	U 0
	ä) t < t1: i1(t) Y(t x)			dx, t > t1: i1(t) 1 Y(t x)			dx + (U1 – U0)Y(t – t1) ;
	0	t1			0	t1

t

å) t < t1: i1(t) UmY(t) – Y(t x)U m sin x dx ;

0

t1

t > t1: i1(t) UmY(t) – U m Y(t x)sin x dx.

0

Например, для цепи варианта à при напряжении вида á имеем при t < t1

t

1

t

U 0

U 0

U 0

t

i1(t)

1 e

dt

t –

1 e

r

t

rt

rt

0

1

1

1

è ïðè t > t1

i1(t) U 0 r

						t1			t t1
)1				e
	t		1				, e			.
)
	1						,
(							+

1

t

5. Для цепи варианта ã переходная проводимость Y(t)

e

, так что можем за-

r

писать при t < T/4

t

1

t x

U

1

1

t

i1(t)

U m cos x dx

m

e

)

cos t

sin t

e

, ,

r

r (

2

2

0

) (

,

+

ïðè T/4 < t < T/2

T 4

1

t x

U m

t

T 4

t

1

t x

i(t) 0

T 4

U m e

cos x dx

–

e

U m

e

cos x dx

r

r

2r

2

2

è ïðè t > T/2

T 4

1

t x

U m

t

T 4

T 2

1

t x

U m

t T 2

i(t)

U m e

cos x dx –

e

U m e

cos x dx –

e

.

r

2r

2r

2r

0

T 4

6. Представляя напряжение u(t) на входе цепи в виде последовательности прямоугольных импульсов напряжения амплитудами u(t) и длительностью õ, запишем ток, обусловленный действием в момент времени t одного импульса напряжения: i(t) Y (t – x)u(x) x + Y(0)u(t). Здесь первое слагаемое определяет ток при t > 0 после окончания действия импульса, а второе слагаемое — ток во время действия импульса. Суммируя токи от всех импульсов при t > 0 и переходя к пределу при õ 0, получаем искомое выражение

t

i(t) u(t)Y(0) + Y' (t x)u(x)dx.

0

514 Ответы на вопросы, решения упражнений и задач

12.3. Расчет переходных процессов в цепях при действии последовательности импульсов

УПРАЖНЕНИЯ

1. Учитывая, что цепь содержит один реактивный элемент и действующие на ее входе импульсы имеют прямоугольную форму, можем решать разностное уравнение

xâûõ [n + 1] xâûõ [n]exp(–T/ ) + xâõ [n](h(T) – h(T – Tè)) a xâûõ [n] + b xâõ [n],

ãäå xâûõ [n + 1] uC [n + 1], xâõ [n] U0·1[n], h(t) — переходная характеристика цепи.

		r2				t			r1r2C
Òàê êàê h(t)				1 e				, ãäå			, òî
	r	r							r	r
1		2							1	2

r2

T

Tè

b h(T) – h(T – T

) h(t)

e

e

1

.

è

r1 r2

Решение полученного уравнения имеет вид

1 e

nT

T

Tè

1)(1 e

nT

uC [n] U

U

r

(e

)

0 b

0 2

e

.

1 e T

r

r

T

1

2

1

e

Подставляя численные значения, находим uC [n] 7(1 e 1,25n ) В. При действии

на входе цепи последовательности мгновенных импульсов напряжения постоянной интенсивности получаем

T

nT

u [n]

K

e

(1 e

)

5(1 e 1,25n ) B.

C

r C

T

1

1 e

2. Обозначим через n номер импульса и номер промежутка времени, следующего за этим импульсом. В моменты действия импульсов ток получает приращение

i KY(0)−(t), ãäå Y(0) — переходная проводимость Y(t) 1r (1 e t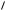 ), найденная

ïðè t 0 (здесь L/r). Учитывая, что i KY (0) K/L, получаем соотношение, связывающее ток в цепи в моменты времени (n – 1)T + 0 è ( n – 1)T – 0: i [(n – 1)T + 0] i [(n – 1) T – 0] + + K/L, n 1, 2, ... В промежутке времени n ток в цепи равен i (t) i [(n – 1)T + 0] exp (–T/ ) { i [(n – 1)T – 0] + K/L} exp (–t/ ), n 1, 2, ...

Таким образом, в конце промежутка времени с номером n ток равен i(nT – 0) {i[(n – 1)T – 0] + K/L} exp (–T/ ).

Òàê êàê i(–0) 0, то можем, принимая последовательно n 1, 2, ..., записать i (T – 0) (K/L) exp (–T/ ), i (2T – 0) (K/L)[exp (–T/ ) + exp (–2T/ )], i (3T – 0) (K/L) [exp (–T/ ) + exp (–2T/ ) + exp (–3T/ )], ... i (nT – 0)

(K/L) exp( nT (K/L)[exp (–T/ )]1 [exp( nT )], n 0, 1, 2, …
n	1 [exp( T )]

Ответы на вопросы, решения упражнений и задач 515

В начале n-го промежутка времени ток в цепи равен

i (nT + 0) i (nT – 0) + K/L (K L) 1 {exp[ (n 1)T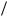 )]}. 1 exp( T )

Здесь в выражениях для i (nT – 0) è i (nT + 0) значение n 0 соответствует первому импульсу (при t 0), n 1 — второму и т. д.

Для заданных численных значений находим 2 10–3 ñ, K/L 5 10–3 À

i (nT – 0) 2,9 10–3[1 – exp (–n)], i (nT + 0) 7,9 10–3{1 – exp [–(n + 1)]}. В промежутках времени между импульсами ток в цепи

i (t) i (nT + 0) exp (–t/ ) 7,9 10–3 [1 e (n 1) ]e t (ðèñ. P12.1).

Âустановившемся режиме при n получаем

i( T – 0) (K/L)[exp (–T/ )][1 – exp (–T/ )]–1

2,9 10–3 À, i ( T + 0) 7,9 10–3 À.

3. à) f(z) 1; á) f(z) (1 + z)/z ; â) f(z) (1 + z + z2)/z ;

ã) f(z) z/(1 + z); ä) f(z) z(1 z). Ðèñ. P12.1 1 z2

4. à) U(z) U

z

U

z

U

z (1 e T )

;

0

z 1

0

z e T

0

(z 1)(z e T )

á) u(t) U

sin t U

ej t

e j t

;

m

m

2 j

U(z)

U

m

z

z

U

zsin T

;

z e j T

m

1 2zcos T z2

2 j z ej T

â) U(z) aT 2 z(1 z). (z 1)3

5. Используя решетчатую функцию f [n] 1, –1, 1, –1, …, представим действующее на входе цепи напряжение в виде u[n] U0 f [n], z-изображение которого

U(z) U0 z/(1 + z) (см. решение упр. 3, вариант ã).

t

iL (t)

1

(1 e

Записывая выражение для переходной проводимости Y(t)

),

U 0

r1

находим:

1

t

1

t Tè

1

Tè

t

h (t)

(1 e

)

1 e

e

1

e

,

è

r

r

r

1

1

1

1

Tè

nT

1

TÈ

T

1

h [n]

e

1

e

, H (z)

e

1

e

.

z e T

è

r

è

r

1

1

Искомый ток имеет своим z-изображением функцию

516 Ответы на вопросы, решения упражнений и задач

U 0

Tè

T

z

IL(z) Hè(z)U(z)

e

1

e

,

r

(z 1)(z e T )

1

которой соответствует решетчатая функция

Tè

T

T

n 1

i [n]

U 0

e

1

e

( 1)

e

,

r

T

L

1

1 e

корни полинома знаменателя IL(z) равны

e

Tè

T

(z )

e

T

H (z

T

z

1

–1, z

2

, G(z

) –1, G(z

)

e

, H

1

,

2

) 1 e

.

1

2

1

Подставляя численные значения, получаем iL[n] 0,83(–1)n – 1 + 0,83e–2,4n À.

13.1. Уравнения и системы параметров четырехполюсников

ВОПРОСЫ

7. Так как любая из пар величин U1, I1, U 2 , I 2 может входить в левую (либо пра-

вую) часть уравнений четырехполюсника, то полное число вариантов уравнений, или, что то же, систем параметров четырехполюсника равно числу соче- таний из четырех элементов по два, что составляет 6. Наиболее распространенными являются системы A-, Z-, Y- è H-параметров.

УПРАЖНЕНИЯ

3. Для нахождения параметров четырехполюсника можно: à) записать уравнения законов Кирхгофа и после их преобразования приравнять коэффициенты при величинахU, I к соответствующим параметрам; á) найти сопротивления че- тырехполюсника в режимах холостого хода и короткого замыкания и, используя известные соотношения, рассчитать искомые величины.

Представим четырехполюсники варианта à в виде как на рис. P13.1. Записав уравнение второго закона Кирхгофа U1 U 2 + I 2 Z, с учетом

соотношения I1 I 2 , найдем A 1, B Z, C 0, D 1. Матрица À-ïà- Ðèñ. P13.1 раметров суть

A	1	Z	.
	0	1

Для получения Y-параметров запишем уравнения в виде I 2 Z1 U1 Z1 U 2 ,

I1 Z1 U1 Z1 U 2 , откуда находим

Y	1			1				.
			1
	Z		1
				1

Записывая входящее в матрицы A, Y сопротивление Z в комплексной форме, можем найти искомые параметры каждого из четырехполюсников варианта à.

Ответы на вопросы, решения упражнений и задач

517

Для цепей варианта á (рис. P13.2) из уравнений законов Кирхгофа U1 U 2 , I1 Z1 U 2 I 2 получаем

A	1	0	.
	Y	1		Ðèñ. P13.2

После преобразования уравнений к виду U1 I1Z – I 2 Z, U 2 I1Z I 2 Z находим

Z	1			1				.
			1
	Y		1
				1					Ðèñ. P13.3

Для цепей варианта â (рис. P13.3) из уравнений законов Кирхгофа I1 I 0 + I 2 , U1 I1Z + U 2 , U 2 Y1 I 0 находим выражения U1 U 2 (1 + 2Y) + I 2 Z, I1 U 2 Y + I 2 , из которых следует:

										A			1 ZY								Z				.
															Y						1
																														1			–	1			,
После преобразования уравнений законов Кирхгофа к виду I																												1			U	1			U	2
																														Z				Z
						1
			1
I	2			U	1	–		Y U	2	находим Y-параметры:
			Z			Z
												1								1
										Y		Z								Z							.
																	1
												1
																				Y
												Z					Z
Аналогично получаем матрицу
													Z				1					1
										Z						Y					Y					.
															1							1
														Y							Y

Для нахождения H-параметров преобразуем уравнения законов Кирхгофа к виду U1 I1Z + U 2 , I 2 I1 – U 2 Y. Матрица H-параметров

H	Z	1	.
	1	Y

Для четырехполюсников варианта à Z-параметры не существуют, не существует также Y-параметров четырехполюсников варианта á.

ЗАДАЧИ

1. À-параметры симметричного четырехполюсника можно найти из соотношений Z1ê BA, Y10 Y10 CA, A2 – BC 1 (Z1ê — входное сопротивление в режиме

518 Ответы на вопросы, решения упражнений и задач

короткого

замыкания, Y10 — входная

проводимость в режиме

холостого хода):

A (1 – Z

Y )–2, B Z

1ê

A, C Y

10

A.

1ê

10

Для варианта à получаем

Z1ê

2Z1Z 2

, Y10

2(Z1 Z 2 )

, A

2Z1 Z 2

, B 2Z1, C

2(Z1 Z 2 )

.

2Z1 Z

2

Z 2 (2Z1 Z 2 )

Z 2

Z 22

Z-параметры находим из соотношений Z11 Z10

Z 2 (2Z1 Z 2 )

, Z22 –Z20 –Z10,

2(Z1 Z 2 )

Z12 –Z21

(Z1ê Z11)Z 22

.

Аналогично Y-параметры получаем, используя соотношения

Y

1

1

–Y

–Y

–Y

Y

11

1ê

+

, Y

22

2ê

11

, Y

12

21

(Y Y )Y

22

.

Z 2

2Z1

10

11

Отметим, что если некоторая система параметров четырехпролюсника получена (например, на основе опытов холостого хода и короткого замыкания), то для нахождения других систем параметров можно воспользоваться связывающими эти системы соотношениями.

Для варианта á находим

Z1ê

2Z1Z 2

, Y10

2

, A

Z1 Z 2

, B

2Z1Z 2

, C

2

.

Z

Z

Z

Z

Z

Z

Z

2Z

1

Z

2

1

2

1

2

1

2

1

Z

2

4Z(1 ZY0 )

Для варианта â получаем Z1ê

, Y10

Y0

, A

1 2ZY0

.

2ZY

1 2ZY

0

1

0

1 2ZY

0

Записывая уравнения законов Кирхгофа для цепи варианта ã

U1 I1 j L1 – I 2 j M, U 2 I1 j M – I 2 j L2,

находим Z11 j L1, Z12 –j M, Z21 j M, Z22 –j L2. Используя соотношения

между Z, Y è À- параметрами, получаем:

j

L2

M

1

L

j (L L

M 2 )

Y

,

A

1

1

2

.

M L

1

L2

(M 2

L L )

M

j

1

2

1

Аналогичный подход позволяет найти матрицы Z-, Y- è À-параметров для цепи

варианта ä

Z j

L1 L2 2M (L2 M)

,

L2 M

L2

Y

1

L2

(L2

M)

,

j (L L

2

M 2 )

L

2

M

(L

L

2

M)

1

1

A

1

L

L

2

2M j (L L

2

M 2 )

1

1

.

L2 M

1 j

L2

Ответы на вопросы, решения упражнений и задач

519

Для цепи варианта å имеем
Z		j L1 r ( j M r)				.
		j M r ( j L2 r)

2. Условные положительные направления токов и напряжений принимаем такими же, как и на рис. Р13.1. Записывая уравнения законов Кирхгофа

U	I	j L	1	I	2	j M +U	N1	,	U	2	I	j M I	2	j L +U
1	1										1			2	N 2

и подставляя в них величины

U

I

Z

I

Z ,

U

I

Z

+ I

Z

,

N1

1

N 11

2

N 12

N 2

1

N 21

2

N 22

получаем

U

I

(j L + Z ) + I

(Z

– j M),

U

I

(Z

+ j M) + I

(Z

– j L ).

1

1

1 N 11

2

N 12

2

1

N 21

2

N 22

2

Матрица коэффициентов этой системы уравнений суть искомая матрица Z-па- раметров.

3. Обозначим À-параметры четырехполюсника N с индексом N (AN, BN, CN, DN).

Учитывая соотношения U

U

N1

, I

I

+ U

j C, U

U

N 2

, I

2

I

N 2

(вариант à),

1

1

N1

1

2

переписываем уравнения

U N1 ANU N 2 + BNI N 2 , I N1 CNU N 2 + DNI N 2

â âèäå U1 ANU 2 + BN I 2 , I1 ( j CAN + CN)U

2 + ( j C BN + DN)I 2 .

Из последних уравнений видно, что

A AN , B BN , C j CAN + CN , D j CBN + DN .

Для четырехполюсников вариантов á è â получаем аналогично

A

AN j LCN

BN j LDN

,

A

AN

AN r BN

.

CN

DN

CN CN r DN

13.2. Схемы, эквивалентные четырехполюснику

ВОПРОСЫ

1. Количество независимых параметров симметричного четырехполюсника равно двум, однако простейшая эквивалентная схема такого четырехполюсника не может содержать два элемента: она содержит либо один (Y0 в Т-образной схеме или Z0 в П-образной схеме), либо три элемента (в Т-образной схеме при этом Z1 Z2, а в П-образной схеме — Y1 Y2). Поэтому нельзя утверждать, что число элементов простейшей эквивалентной схемы четырехполюсника всегда равно числу его независимых параметров.

УПРАЖНЕНИЯ

5. Приравнивая À-параметры Т- и П-образных схем, эквивалентных четырехполюснику, получаем 1 + Z1Y0 1 + Y2Z0, Z1 + Z2 + Z1Z2Y0 Z0, Y0 Y1 + Y2 + Y1Y2Z0,

1 + Z2Y0 1 + Y1Z0, откуда находим Z0 Z1 + Z2 + Z1Z2Y0, Y1	Z 2Y0	, Y2	Z1Y0	.
	Z 0		Z 0

520 Ответы на вопросы, решения упражнений и задач

Для заданных вариантов получаем: à) Z0 2r, Y1 0, Y2 0 (ðèñ. P13.4, à);
á) Z			gL	, Y	1	, Y		j C, (ðèñ. Ð13.4, á);
	0						2
			C	1	j L
â) Z0 Z1 j L, Y1 0, Y2								Y0 g j C (в последнем случае Т- и П-образные
схемы совпадают).

6. Параметры эквивалентных четырехполюснику схем можно найти различными способами: à) приравнивая коэффициенты при напряжениях и токах уравнений законов Кирхгофа, составленных для исходного четырехполюсника и его эквивалентной схемы; á) вычисляя параметры четырехполюсника (например, À-параметры) и определяя далее искомые параметры эквивалентных схем с помощью известных соотношений; â) преобразуя соединения элементов четырехполюсника к аналогичному соединению Т- или П-образных схем.

Для условия варианта à получаем Z1 Z3, Z2 43Z , Y0 Z3 (Т-образная схема) (рис. P13.5, à) è Z0 3Z, Y1 34Z , Y2 31Z (П-образная схема).

Для условия варианта á имеем: Z1 43Z , Z2 43Z , Y0 Z3 (Т-образная схема) (рис. P13.5, á) è Z0 8Z, Y1 21Z , Y2 21Z (П-образная схема).

Ðèñ. P13.4 Ðèñ. P13.5

À-параметры четырехполюсника варианта â были найдены при решении зада- чи 1, §13.1:

A

Z1

Z 2

, B

2Z1Z 2

, C

2

, D A. Учитывая связи между А-параметра-

Z

1

Z

2

Z

1

Z

2

Z

Z

1

2

ми четырехполюсника и параметрами его эквивалентных схем, получаем, в част-

ности, Y1 Y2

A 1

1

, Z0 B

2Z1Z 2

(П-образная схема).

B

Z

Z

1

Z

2

1

7. Òàê êàê À

C, Z1 Z2

1

BC 1

(Т-образная схе-

BC 1, то получаем: Y0

C

BC 1

ìà), Z0 B, Y1

Y2

1

BC 1

(П-образная схема).

B

BC 1

8. Запишем уравнения четырехполюсника в системе A-параметров:U

AU

+ BI

,

1

2

2

I CU

2

DI

. Åñëè U

const è I

const, à U

var, òî A 0, таким ообразом

1

2

1

2

2

U1 BI 2 . Для Т-образной схемы имеем A 1 + Z1Y0 0, Z1 –1/Y0 –Z0 , è ïðè

Ответы на вопросы, решения упражнений и задач

521

Z1 jx1 получаем Z0 –jx1. Пусть, например, Z1 j L, тогда Z0 1 j C. Ïðè ýòîì B Z1 + Z2 + Z1Z2Y0 Z1 è I 2 U1 Z1, т. е. параметры четырехпо-

люсника не зависят Z2. Эквивалентная Т-образная схема изобра-
жена на рис. P13.6. Полученное выражение для тока I 2 справед-
ливо при любом сопротивлении Zïð и, следовательно, ток I 2	íå
зависит от Zïð.	Ðèñ. P13.6

13.3. Экспериментальное определение параметров четырехполюсника

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Два четырехполюсника неразличимы при выполнении опытов холостого хода и короткого замыкания при любой частоте напряжения, если они содержат только резисторы. В общем случае параметры четырехполюсников, содержащих катушки индуктивности и конденсаторы, не могут быть одинаковыми при любой частоте напряжения. Поэтому они различимы при выполнении опытов холостого хода и короткого замыкания при различных частотах напряжения и неразли- чимы при частоте 0 .

4. Выражения Z1ê

B

, Y10

C

, Z2ê

B

, Y20

C

, AD – BC 1 позволяют получить

A

D

D

A

соотношения

Z1ê

Y20

, A

Z1ê

, B Z2êA, D

Z 2ê

A, C Y20D.

Z 2ê

Y10

Z 2ê (1 Z 2êY20 )

Z1ê

Для нахождения À-параметров несимметричного четырехполюсника достаточно рассчитать три величины из четырех Z1ê, Z2ê, Y10, Y20. Если четырехполюсник симметричный, то учитывая соотношения Z1ê Z2ê, Y10 Y20, можно ограничить-

ся расчетом двух величин, например, Z2ê, Y20.

2 LC 1

1

, Z2ê

L C

1

, A

Для варианта 1à находим: Z1ê

, Y20

,

j C

2 LC

1

1

j( L 1 C)

j L

B

, C

, D 1.

j C

j L

jr L

r j L

Для варианта 3à имеем: Z1ê r, Z2ê

, Y20

1

, A

, B r, C

1

,

r j L

j L

j L

j L

D 1.

Четырехполюсники вариантов 1â, 2â, 3â симметричны, поэтому для нахождения их À-параметров достаточно предварительно рассчитать две величины, например Z1ê Z2ê è Y10 Y20 , и далее найти искомые параметры, используя приведенные ранее соотношения.

Для варианта â-1 получаем: Y10

j C

, Z1ê

j L

2 2 LC

, A 1 – 2LC,

1 2 LC

1

2 LC

B j L(2 – 2LC), C j C, D A 1 – 2LC.

5. Рассчитывая предварительно величины Y10, Z1ê с помощью соотношений

Y

I1

e j!1 , Y

I 2

e j!2 , ãäå !

arccos

P1

, !

arccos

P2

, можем найти

10

1ê

1

U1I

2

U 2 I 2

U1

U 2

1

522 Ответы на вопросы, решения упражнений и задач

À-параметры четырехполюсника, используя полученные при решении предыду-

щего упражнения выражения: A		1		, B Z1ê A, C Y10 A, D A.
		Y10 Z
1			1ê

6. Подключим к выходным зажимам четырехполюсника сопротивление Zí и измерим величины I1, U1, I 2 . Из уравнений U1 (AZí + B)I 2 , I1 (CZí + D)I 2 , AD – BC 1, D A можем найти параметры симметричного четырехполюсника.

Если четырехполюсник несимметричный, то три записанные выше уравнения следует дополнить еще одним, получаемым при выполнении еще одного опыта. Подключая, например, к выходным зажимам четырехполюсника сопротивление

Z	и измеряя величины U		,	I	, получаем недостающее соотношение
í	(AZ	1		2
U		B)I .
1	í	2

13.4. Соединение четырехполюсников

УПРАЖНЕНИЯ

4. Рассматривая каждый из четырехполюсников вариантов à, á è â как образованный каскадным соединением более простых четырехполюсников, À-парамет- ры которых известны, можем получить искомую матрицу перемножением матриц À простых четырехполюсников. Для варианта à имеем:

A A	A	2	A	3				1 0			1 Z 2						1 Z1Y Z1 Z 2 Z1Z 2Y					.
						1 Z1
1						0 1		Y	1		0 1						Y	1 Z 2Y

Схему четырехполюсника варианта á рассматриваем как полученную каскадным соединением двух Т-образных четырехполюсников с элементами Z1,Y, 0,5Z2 è 0,5Z2,Y, Z1:

		1 Z Y Z				Z 2				Z1Z 2Y				1	Z 2		Y		Z 2	Z						Z1Z 2Y
				1																			1
A		1			2						2					2			2								2
									Z 2															Z1
		Y			1						Y			Y						1							Y
									2															2
		2Z Y Z Y Z Z Y 2 2Z Z 2Z Z Y 2Z 2Y Z 2 Z Y 2																															.
	1
		1	2				1		2			1		2				1	2					1			1	2
		2Y Z Y 2												1 2Z Y YZ							2	Z			1		Z Y 2
					2												1										2

Четырехполюсники вариантов ã, ä è å рассматриваем как образованные при параллельном соединении двух четырехполюсников с матрицами параметров Y1, Y2.

Для варианта ã получаем:

													1 Z1Y				1
Y1		1				1	1		,	Y2			2Z	1 Z12Y		2Z1	Z12Y		,
		Z	2			1	1							1		1 Z1Y
													2Z1 Z12Y			2Z1	Z12Y

Ðèñ. P13.7