книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Ответы на вопросы, решения упражнений и задач

503

2. à) Применяя метод наложения, представляем напряжение в виде суммы двух скачкообразных напряжений U0(t – t1) è –U0(t – t2) и записываем искомое изо-

бражение U(p) Up0 e pt1 Up0 e pt2 Up0 (e pt1 e pt2 ), учитывая, что изображе-

ние скачкообразного напряжения U0 åñòü U0/p. Вычисляя интеграл Лапласа, получаем тот же результат:

		t2
	U(p) u(t)e pt dt U 0 e pt dt		U 0	(e pt1	e pt2 ).
			p
	0
		t1

Если длительность t2 – t1 t действия импульса напряжения стремится к нулю, а его амплитуда возрастает, так что произведение U0 t сохраняется постоянным, то в пределе при t 0 изображение принимает вид

	U(p)	U	0	lim	e pt1 e pt2	t U		te pt1 .
		p			t		0
				t2 t1

3, 4. Воспользуемся изображением производной f (t) функции f(t):

f' (t)e pt dt pF(p) – f(0).

0

Ïðè p имеем lim pF(p) lim [f(0) + f' (t)e pt dt] f(0), à ïðè p 0
p	p
	0
	lim pF(p) f (0) f (t)			f ( ).
	p 0		0

5. à) i (+0) 0, i ( ) U0 /2r ; á) i (+0) U0/r, i ( ) 0; â) i(+0) U0/r, i( ) U0/r ; ã) i (+0) 0, i ( ) 0; ä) i (+0) U0/r, i ( ) 0.

10.2. Расчет переходных процессов операторным методом

ВОПРОСЫ

1.При расчете переходных процессов операторным методом токи в катушках индуктивности и напряжения на конденсаторах в момент времени t +0 входят в уравнения второго закона Кирхгофа и учитываются, таким образом, на начальной стадии решения задачи, а именно на этапе составления уравнений в операторной форме. При расчете переходных процессов классическим методом на- чальные условия (токи в катушках и напряжения на конденсаторах) учитывают уже после составления и решения уравнений, а именно на этапе нахождения постоянных интегрирования, входящих в решение дифференциальных уравнений цепи.

2.В общем случае при ненулевых начальных условиях ток I(p) на входе двухполюсника нельзя представить в виде I(p) U(p)/Z(p), ãäå U(p) — операторное изображение входного напряжения. Поэтому операторное сопротивление Z(p)

нельзя получить, заменив в выражении Z(j ) комплексного сопротивления двухполюсника величину j на оператор p. Однако при нулевых начальных

504 Ответы на вопросы, решения упражнений и задач

условиях из выражения I(p) U(p)/Z(p) можно найти операторное сопротивление Z(p) U(p)/I(p), которое совпадает с комплексным сопротивлением Z(j ) после замены в нем величины j на оператор p.

4. При нулевых начальных условиях уравнения законов Кирхгофа можно полу- чить, заменяя в соответствующих уравнениях комплексного метода комплексные токи I, напряженияU, сопротивления Z и проводимости Y на величины I(p), U(p), Z(p), Y(p). Обратное также справедливо: записав уравнения законов Кирхгофа, можем, принимая начальные условия нулевыми, перейти к уравнениям в комплексной форме после замены в них оператора p на величину j .

7. Если полином H(p) операторного изображения тока I(p) G(p)/H(p) не имеет комплексных корней, то все коэффициенты G(p)/H(p) вещественные. Если же он имеет хотя бы одну пару комплексно-сопряженных корней p1 – + j è

p2 – – j , то коэффициенты À(ð1) G(p1)/H (p1), A(p2) G(p2)/H (p2), входящие в выражение искомого тока i(t) exp (– t)[A(p1) exp (j t) + A(p2) exp(–j t)]

в общем случае, когда A(p1) A(p2), должны быть комплексными, так как только тогда ток i(t) будет вещественным.

8. Из уравнения Z(p)I(p) U(p), в котором I(p) — ток на входе двухполюсника, Z(p) — его операторное сопротивление, следует, что полином Z(p) совпадает с характеристическим полиномом соответствующего дифференциального уравнения цепи. Действительно, переход от дифференциального уравнения цепи к характеристическому выполняется так же, как и переход от дифференциального уравнения к операторному, а именно путем замены k-й производной тока на k-ю степень величины (при составлении характеристического уравнения) либо на k-ю степень оператора p при получении операторного уравнения. В последнем случае начальные условия можно всегда принять нулевыми, так как свойства цепи не зависят от задаваемых начальных условий. При расчете операторного сопротивления цепи токи всех катушек индуктивности и напряжения на всех конденсаторах следует принять равными нулю, все источники ЭДС должны быть замкнуты накоротко, а ветви с источниками тока — разорваны.

УПРАЖНЕНИЯ

1. Операторные сопротивления цепей соответствующих вариантов равны:

à) Z(p)

r r

pL(r r )

; á) Z(p)

r pL p2 rLC

; â) Z(p)

r pL p2 rLC

1 2

1

2

;

r pL

rCp 1

(r pL)Cp

2

ã) Z(p)

pL(prC 1)

; ä) Z(p)

r pL

; å)

Z(p)

r pL p2 rLC

.

Cp(r pL)

1

(r

pL)pC 1

p2 LC

1

2. Изображенным на рис. Р10.1 схемам электрических цепей соответствуют записанные в операторной форме уравнения законов Кирхгофа:

à) Ir (p) IL(p) + IC (p), rIr (p) + pLIL(p) E(p) + LiL(0), pLIL(p) – Cp1 IC (p)LiL(0) + Ep + uC p(0).

Ответы на вопросы, решения упражнений и задач

505

á) IC (p) =(p) + IL(p), pLIL(p) + Cp1 IC(p) LiL(0) – uC p(0).

ä) IL(p) IC(p) + I r1(p), =(p) + I r1(p) I r2(p), IL(p)pL + IC (p)Cp1Ep + LiL(0) – uC p(0), I r1(p)r1 + I r2 (p)r2 – IC (p)Cp1 uC p(0).

Ðèñ. Ð10.1

4. Учитывая, что операторное изображение ЭДС и тока заданных источников

cóòü E(p)

E m

=(p)

= m

,

, получаем:

p2 2

p2

2

E m [(r1 r2 )Cp 1]

E m Cp

á) I(p)

; â) I(p)

;

(p2 2 )r (r Cp

1)

(p2

2 )(p2 LC 1)

1

2

ã) I(p)

E m (r1 r2 pL)

;

ä) U(p)

J m r

;

(p2

2 )r (pL r )

(p2

2 )(prC 1)

1

2

å) U(p)

= m rpL

; ç) I(p)

E m (pL r)

.

(p2

(p2 2 )[(r

2 )(pL r)

r )pL r r ]

1

2

1

2

5. Учитывая заданные начальные условия iL(–0) 0, uC (–0) U0 120 В при составлении уравнений законов Кирхгофа в операторной форме

I1(p) I 2 (p) I 3 (p) 0,

rI

(p)

I 2 (p)

U 0

uC (0)

,

1

Cp

p

p

I

(p)pL

I 2 (p)

uC (0)

3

Cp

p

и решая их относительно тока I2(p), получаем:

I	2 (p)	u	C	(0)rC		4,8 10	2
							.
		p2 rLC pL r				4 10 5 p2 0,1p 40

Решая уравнение H(p) 0, получаем p1 –2000, p2 –500. Далее находим G(p1)G(p2) –4,8 10–2, H (p1) –0,06, H (p2) 0,06 è òîê i2(t) 0,8e–2000t – 0,8e–500t А. Далее получаем:

506 Ответы на вопросы, решения упражнений и задач

1

t

uC(t) C 0 i2 (t)dt + uC(0) –40e–2000t + 160e–500t, i3(t) 3 + 0,2e–2000t – 3,2e–500t À,

i1(t) 3 + e–2000t – 4e–500t À.

7. Раскладывая выражения I(p) на простые дроби, находим:

U 0

B

C

U 0

0,25

à) I(p)

)

Ap

,

)

0,25p 0,75

,

,

p

p 3

r

((p 1)2

3+

r

( (p 1)2

+

i(t)

U 0

[e t

2te t e 3t ];

4r

á) i(t)

U 0

(1 0,25e 0,5t );

r

2p 1

Ap B

C

â) I(p) U

0

U 0 )

,

(p2

2 )(p

2)

2

p

( p2

2+

U

3p 2 2 2

3

,

0 )

,

2 )(p2

((4

2 ) (4 2 )(p

2)+

i(t)

3U

0

cos t

(2

2 2 )U

0

sin t

3U

0

2t .

e

4

2

(4

2 )

4 2

8. Подставляя в выражение I(p)

U(p)

изображениеU(p)

U m

входного на-

p

r pL

пряжения, получаем ток I(p)

U m

, ãäå −

r

,

L(p )(p −)

L

i(t)

U m

(e t e−t ).

r L

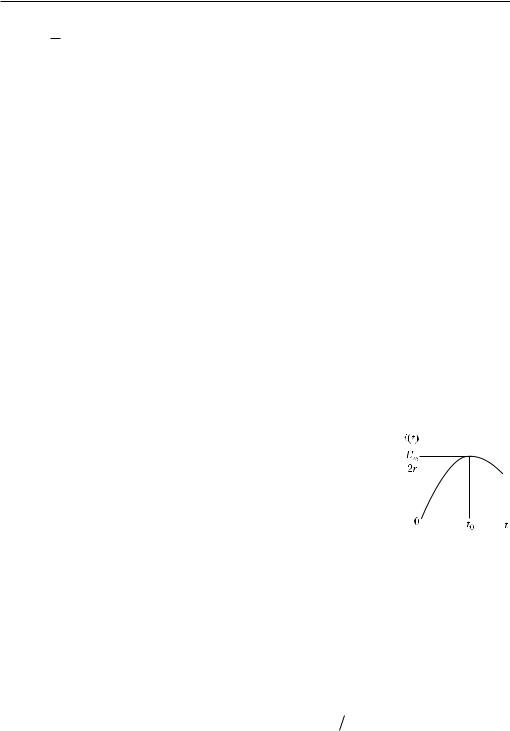
Зависимость i(t) ïðè − 2 изображена на рис. Р9.5. Ток i(t)

достигает

наибольшего

значения,

равного

U m

,

ïðè

2r

Ðèñ. Ð9.5

1

−

0,3

t

ln

Γ

c.

0

−

9. Записываем уравнения

r i

L

di1

M

di2

U

,

1 dt

dt

1 1

0

r i

M

di1

L

di2

0

2 dt

2

2

dt

в операторной форме

(r1 pL1)I1(p) MpI 2 (p) U 0

p,

MpI1(p) (r2

L2 p)I 2 (p) 0

Ответы на вопросы, решения упражнений и задач

507

и, вводя обозначения −																	r					,−							r		,Κ 1 k2 , k2																		M			2
																		1												2																								, после простых пре-
											1													2
																L1													L2																			L1L2
образований получаем:																					U 0														− 2				p
										I1(p)																																									,
																					pL					[Κp2 (−									1	−					2	)p − −					2		]
																					1																								1
										I 2 (p)																									U 0 M																		.
																							L L					[Κp2							(−					−				)p − −
																											2										1						2								2	]
																								1																							1
Используя теорему разложения, находим величины
		U		0			U		0			Κp			2							p t										Κp							p t															U	0	M		p t		p t
i (t)										1								e 1								1								1		e					2	,	,	U		(t)												(e 1	e	2	),
																																													2
1		r					bL			)			−																			−																						bL L
														2																				1								+															2
			1						1	(																																													1
ãäå b (−			1		−		2	)2		4k2		− −				2		,				p					[ (−						1		−			2		) b]						2Κ.
													1								1,2

В частных случаях токи i1(t), i2 (t) выражаются более простыми формулами.

Например, при −1

− 2 − имеем

U 0

U 0

−

t

−

t

U 0

−

t

−

t

i (t)

e

1 k

e

1 k

,

i

(t)

e

1 k

e 1 k

.

1

r

2r

2

2 r1r2

1

1

Ïðè k 1, ò. å. ïðè M 2 L L

2

, получаем

1

i (t)

U 0

U 0

− 2

ep1t , i

(t)

U 0

ep1t .

2

1

r1

r1 −1

− 2

M(−1 − 2 )

Åñëè ïðè ýòîì r1 r2

r è L1 L2

L, òî

U

1

−

t

U

−

t

1r 2 2 2 2r 2

10.Введем обозначения G(j ) G( ) exp [ j ( )], N(j ) N( ) exp [ j ( )]. Òî- гда получаем: 0 e .i (t) 0 1 e , i (t)

G( j )

ej t

G( j )

e

j t

G( )ej ( ) ej t

G( )e j ( ) e j t

H' ( j )

H' ( j )

2 j N ( )ejΠ( )

2 j N ( )e jΠ( )

G( )[ej[ t ( ) Π( )] e j[ t ( )Π( )]]

G( )sin[ t ( ) Π( )]

2 j N ( )

N ( )

G( )ej ( )

G( j )

Im )

ej t

,

Im )

ej t , .

N ( )ejΠ( )

N ( j )

+

+

(

(

11.1. Частотные характеристики непериодических сигналов

ВОПРОСЫ

5. Как видно из амплитудной частотной характеристики U( ) 2U0 sin aΘ

прямоугольного импульса длительностью 2a (см. рис. Р11.1), при уменьшении

508 Ответы на вопросы, решения упражнений и задач

длительности импульса ширина ее первого лепестка увеличивается, а амплитуда падает. Это означает, что ширина полосы частот, в пределах которой заключена основная часть энергии сигнала, увеличивается. Таким образом, длительность импульса и ширина той части его спектра, в которой заключена большая часть энергии сигнала, связаны обратно-пропорциональной зависимостью. Такая связь существует не только для прямоугольных импульсов, но и для сигналов других форм. Говорят, что чем меньше длительность сигнала, тем шире его спектр, понимая под ним полосу частот, определяющих его энергию.

Ðèñ. Ð11.1

УПРАЖНЕНИЯ

2. Частотную характеристику напряжения u(t) можно получить, записывая преобразование Лапласа U(p) и заменяя оператор p на величину j , либо вычисляя интеграл прямого преобразования Фурье. Упростить получение решения можно, представляя напряжение u(t) в виде суммы сдвинутых во времени напряжений, частотную характеристику каждого из которых можно легко рассчи- тать.

Вариант à. Представляя напряжение в виде суммы двух сдвинутых на время 2à ступенчатых напряжений U0 è U0(t – 2a) и записывая их операторные изображе-

	íèÿ U0/p, –U0 [exp (–2ap)]/p, получаем после замены оператора p на величину j
	искомую частотную характеристику U(j )	U 0	(1 – e–2ja ), U( ) 2U0		sin a		,
		j

) arctg cos2a .. sin2a

Амплитудная частотная характеристика U( ) совпадает с характеристикой такого же, но симметрично расположенного относительно начала координат прямоугольного импульса (см. рис. Р11.1).

Вариант á. Используя операторное изображение синуcоидального напряжения, запишем

	U					U					p#
U(p)		m		0			m		0
										e		0
	2	p2				2	p2
	0					0

и находим после замены p j частотную характеристику

Ответы на вопросы, решения упражнений и задач

509

			U m 0						j		#				U m 0					#					#
											0
U( j )								1 e										1 cos			jsin
		2			2										2	2
																				0					0		,
			0												0
а также амплитудную и фазовую частотные характеристики
																				#
		2U m 0							#										sin 0							#
U( )							cos					,		( ) arctg														.
									2 0											#
		02 2																								2 0
																			1 cos			0

7. Сопоставляя спектральную характеристику U(j ) одиночного импульса

T

U( j ) uèìï (t)e j t dt uèìï (t)e j t dt

0

ñдискретным спектром периодического напряжения

T

U( jq 1) u(t)e jq 1t dt,

0

видим, что выражение для расчета величины U(jq .) U(2#q/T) можно полу- чить, выполняя замену на q 1 в выражении U(j ).

11.2. Расчет переходных процессов при помощи частотных характеристик сигналов и электрических цепей

ВОПРОСЫ

3. Метод частотных характеристик позволяет рассчитать переходные процессы в цепях только при нулевых начальных условиях для токов в катушках и напряжениях на конденсаторах. При ненулевых начальных условиях можно, пользуясь линейностью электрической цепи, рассчитать

токи переходного процесса, обусловленные началь-
ными запасами энергии в цепи при отсутствии внеш-
них источников (замкнутых накоротко источниках
ЭДС и разомкнутых ветвях с источниками тока), а
также действием внешних источников при нулевых
начальных условиях. Последний расчет можно вы-
полнить методом частотных характеристик.										Ðèñ. Ð11.2
УПРАЖНЕНИЯ
6. Для варианта à имеем
	2				2				2I1(0)
i(t)			I1( )cos t d				I1(0)cos t d			sin ' t.
	#				#				#t
	0				0
Зависимость i(t) изображена на рис. P11.2.
Для варианта á получаем
				2I1(0)
			i(t)					(1 cos t).
				#t2

510 Ответы на вопросы, решения упражнений и задач

12.1. Переходные и импульсные характеристики электрических цепей

ВОПРОСЫ

5.В промежутках времени между импульсами источник ЭДС должен быть замкнут накоротко, так как его внутреннее сопротивление равно нулю. Ветви, содержащие импульсные источники тока, в промежутках времени между импульсами должны быть разомкнуты, так как внутреннее сопротивление таких источников бесконечно велико.

6.Процессы в цепи в моменты действия импульсов описывают неоднородными дифференциальными уравнениями, тогда как в моменты паузы — однородными, с равной нулю правой частью.

8. При действии импульса катушки индуктивности и конденсаторы накапливают энергию в виде энергии магнитных и электрических полей. После окончания действия импульса токи катушек и напряжения на конденсаторах могут быть не равными нулю, так что в промежутках времени между импульсами протекают переходные процессы, при которых накопленная в этих элементах энергия рассеивается в резисторах.

10. В момент действия импульса тока заряд конденсатора изменяется на величи- ну q I t и напряжение на нем получает приращение u q/C. После оконча- ния действия импульса напряжение на конденсаторе, как и его заряд, остаются неизменными до момента появления следующего импульса тока.

УПРАЖНЕНИЯ

1. Для получения переходных характеристик на вход цепи подаем скачкообразное напряжение и, рассчитывая переходный процесс, находим напряжение u2 (t) è òîê i1(t). После деления их на величину u1 находим искомые характеристики:

r t

à) h(t) e L

â) h(t) 21 e

t

ä) h(t) e rC

1

r

t

r

t

1

r

t

, Y(t)

1 e

L

; á) h(t)

1 e

L

, Y(t)

1 e

L

;

r

r

r

t

1

1

r

t

t

1

t

2L

, Y(t)

1

e

2L

; ã) h(t)

1 e

rC

, Y(t)

e

rC ;

r

2

r

1

t

1

2t

1

2t

, Y(t)

e

rC ; å) h(t)

1 e

rC

, Y(t)

1 e

rC

.

r

2

2r

3. Записывая операторное изображение прямоугольного импульса

	U(p) U0/p – (U0/p) exp (– pT) (U0/p)[1 – exp (– pT)], а также операторное со-
	противление цепи Z(p)	r LCp2 pL	r
		í	í	, получаем операторное изображение
		ríCp 1
								r (1 e pT )
	напряжения на сопротивлении нагрузки Ur (p)				G(p)		U
								0 í		. Äëÿ
					H(p)		p(r LCp2 pL r )
							í		í
	расчета функции ur (t) используем		теорему		разложения. Корни				полинома
	H(p) равны: p1 0, p2 –8,87 105, p3		–1,13 105. Вычисляя значения H (p1),

Ответы на вопросы, решения упражнений и задач 511

H (p2), H (p3), находим искомое напряжение u1r (t) 10–2 + 1,45 10–3e 8,87 105 t –115, 10 2 e 1127, 105 t  ïðè 0 t T è u(t) u2r (t) – u1r (t – T) ïðè t ; T.

4.Указанные интегралы равны à) U0; á) 0; â) 0; ã) 0; ä) 0; å) 0; æ) 1; ç) 0; è) 1; ê) ; ë) U01(t); ì) + .

5.В момент времени действия импульса выходная величина изменяется по закону xâûõ(t) Kh(0)−(t), а после его окончания, для t > 0 — по закону xâûõ(t) Kh−(t).

6.Импульсные характеристики имеют вид:

r

r

t

1

r

t

r

r

t

1

r

t

à) h−(t)

e

L , Y−(t)

e

L

; á) h−(t)

e

L

, Y−(t)

e L

;

L

L

L

L

r

r

t

1

r

t

1

t

1

t

â) h−(t)

e 2L

, Y−(t)

e

2L

; ã) h−(t)

e

rC ϑ Y−(t)

e

rC

rC

r 2C

4L

4L

1

e

t

1

e

t

1

e

2t

1

e

2t

ä) h−(t)

, Y−(t)

; å) h−(t)

, Y−(t)

rC

rC

rC

rC

r

rC

r 2C

rC

2C

;

.

7. В момент действия импульса конденсатор заряжается, причем ток заряда бесконечно велик. К моменту времени окончания импульса (t +0) напряжение на конденсаторе становится равным u(+0) Kh−(0) K/rC. После окончания действия импульса конденсатор разряжается, в связи с чем ток в цепи изменяет свое направление. При t > 0 имеем uC (t) (K/rC) exp (–t/rC), iÑ (t) –(K/r2C) exp (–t/rC).

8. В момент действия импульса имеем u2(t) Kh(0)−(t), i1(t) KY(0)−(t), а после его окончания — u2(t) Kh (t), i1(t) KY (t).

В цепях вариантов à, â, ä имеем h(0) 0, в связи с чем напряжение u2 в момент действия импульса становится бесконечным. Аналогично в цепях вариантов â, ã, ä, å имеем Y(0) 0, и, следовательно, ток i1 в момент действия импульса также становится бесконечным.

В цепях вариантов á, ã, å получаем, как нетрудно проверить, h(0) 0 è âåëè- ÷èíà u2(0) Kh (0) оказывается равной в цепях вариантов á) u2(0) Kr/L; ã) u2(0) K/rC; å) u2(0) K/rC. В цепях вариантов à, á имеем Y(0) 0 è òîê i1(0) равен: à) i1(0) K/L; á) i1(0) K/L.

Искомые величины после окончания действия импульса описываются выражениями:

Kr

r

t

K

r

t

Kr

r

t

K

r

t

à) u2(t) –

e L

, i1(t)

e

L ; á) u2(t)

e

L

, i1(t)

e L

;

L

L

L

L

Kr

r

t

K

r

t

K

t

K

t

â) u2(t)

e

2L , i1(t)

e

2L

; ã) u2(t)

e

rC , i1(t)

e

rC ;

4L

4L

rC

r 2C

K

e

t

K

e

t

K

e

2t

K

e

2t

ä) u2(t) –

, i1(t) –

; å) u2(t)

, i1(t)

.

rC

rC

rC

rC

rC

r 2C

rC

r 2C

512 Ответы на вопросы, решения упражнений и задач

12.2. Расчет переходных процессов в цепях при помощи интеграла Дюамеля

ВОПРОСЫ

1. При условии à) интеграл сохранит свой вид, однако переходную проводимость Y(t) следует рассчитать с помощью соотношения Y(t) ik(t)/U0, где входное напряжение U0 — постоянное. При расчете напряжения uk(t) íà k-ой ветви переходную проводимость в выражении интеграла Дюамеля следует заменить на переходную характеристику h(t) uk(t)/U0.

2. Входящая в интеграл Дюамеля переходная (либо импульсная) характеристика цепи определяется при нулевых начальных условиях. Поэтому непосредственное использование интеграла Дюамеля для расчета токов и напряжений при ненулевых начальных условиях невозможно. Для расчета переходного процесса можно воспользоваться методом наложения, принимая, что искомая величина содержит в переходном процессе две составляющие, одну из которых можно найти с помощью интеграла Дюамеля при нулевых начальных условиях, а другую составляющую, обусловленную начальным запасом энергии в цепи, — любым из рассмотренных ранее методов, например классическим или операторным.

Аналогичный подход можно применить и при расчете переходного процесса, возникающего при подключении активного двухполюсника к внешнему источ- нику с ЭДС (либо током) произвольной формы.

										t
3. При условии à интеграл Дюамеля для t < t						равен i(t) u(0)Y(t)					u Y(t x)dx,
					1						1x
										0
			t1				t
à äëÿ t > t	1	— i(t) u(0)Y(t)		Y(t x)u	dx +			Y(t x)u	dx.
				1x				2x
			0				t1

Условие á означает, что напряжение имеет скачок u u2(t1) – u1(t1) ïðè t t1.

t

Поэтому можем записать при t < t

: i(t) u(0)Y(t) +

Y(t x)u

dx è ïðè t > t

:

1

1x

1

0

t1

t

i(t) u(0)Y(t) +

Y(t x)u

dx + [u

(t

) – u

(t

)]Y(t – t

) +

Y(t x)u

dx.

1x

2

1

1

1

1

2x

0

t1

Входящее в последнее выражение слагаемое uY(t – t1) [u2(t1) – u1(t1)]Y(t – t1) определяет ток в цепи, обусловленный действием скачкообразного напряженияu(t1), подключаемого ко входу цепи в момент времени t1.

УПРАЖНЕНИЯ

4. Для вариантов напряжения u(t) à, á, ä, å выражения для тока i1(t) имеют различный вид при t < t1 è ïðè t > t1, тогда как в вариантах â, ã можно использовать единое выражение для тока при t > 0:

	t	U 0			U 0		t	U 0
	à) t < t1: i1(t) Y(t x)		dx, ux			,	t > t1: i1(t) 1 Y(t x)		dx ;
	0	t1			t1		0	t1