книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

443

дуктивности, и емкости можем представить эквивалентные схемы или в виде рис. 22.6, или в виде рис. 22.7. Обе схемы приближенные, так как в действительности и индуктивность, и емкость являются распределенными. Составляя для схем рис. 22.6 и 22.7 уравнения и решая их для малого отклонения ? от состояния равновесия, получим также различные ответы в отношении точек устойчи- вого равновесия.

Ðèñ. 22.5 Ðèñ. 22.6 Ðèñ. 22.7

Так, например, для схемы рис. 22.6 имеем уравнения:

i

i

i; u

ri L

di

u;

1 t

i dt

u (0)

L

di

u.

0

C

1

C

1

dt

C

C

dt

0

Исключив из них iC è i1, получим

u

rCL

d 2 i

L

di

ri rC

du

u.

0

dt2

dt

dt

du

1

d 2u

2

Принимая i ip

+ ?, имеем u up

?

? и, ограничи-

2

di

2

di

i i

i i

p

p

ваясь первыми двумя членами, находим u uð + rä?. Тогда для малого отклонения ? тока от положения равновесия получаем уравнение

0 rCL

d 2

?

L

d?

r? rr C

d?

r ?

(*)

dt

2

dt

ä

dt

ä

èëè

d 2

?

2−

d?

2

? Ι, ãäå 2−

1

rä

è

2

r rä

.

dt2

dt

0

rC

L

0

rCL

Легко заметить, что уравнение (*) переходит в уравнение, рассмотренное в § 22.2 при Ñ 0, и в уравнение, рассмотренное в § 22.3 при L 0.

Корни характеристического уравнения равны

					1, 2	− − 2 2 .
						0
Åñëè 2		r rä	9 0,	ò. å. r + r		< 0, то оба корня вещественны и один корень
0		rCL			ä

положительный; следовательно, раз возникшее отклонение ? нарастает со временем и состояние неустойчивое. Условию r + rä < 0 отвечает точка À.

444 Часть 3. Теория нелинейных электрических и магнитных цепей

Åñëè 20 8 0, ò. å. r + rä > 0, то состояние характеризуется точкой Â. При этом корни 1 è 2 могут быть вещественными или комплексными. При условии − > 0 вещественные части обоих корней отрицательны, раз возникшее отклонение ? затухает во времени и состояние устойчивое. Ïðè − < 0 состояние неустойчивое.

Составляя аналогичным образом уравнения для схемы на рис. 22.7 и решая их для малого отклонения ? от состояния равновесия, получим уравнение

d 2 ?

d?

2

1

r

2

r rä

2−

? Ι, ãäå 2−

è

0

.

dt2

dt

0

r C

L

r CL

ä

ä

Теперь 20 < 0 ïðè r + rä > 0, и, следовательно, неустойчивой будет точка B. В случае 20 > 0 точка À будет устойчивой ïðè − > 0 è неустойчивой ïðè − < 0.

Итак, в зависимости от выбора эквивалентной схемы ответ получается различным.

Сопоставляя результат, полученный в § 22.3 при L 0, когда устойчивой была точка À, с результатом по схеме рис. 22.6 при L 0, когда точка À оказалась неустойчивой при любом сколь угодно малом, но конечном значении L, видим, что чрезвычайно важно учитывать даже малые параметры. Сопоставление же результатов по рис. 22.6 и 22.7 показывает, что столь же важно правильно отразить в эквивалентной схеме взаимное расположение параметров L è Ñ. Это зависит от характера самого нелинейного элемента. Если он имеет преимущественно индуктивный характер, т. е. в нем энергия магнитного поля преобладает над энергией электрического поля, что, например, наблюдается при электрической дуге, существующей при больших токах и малых напряжениях, то следует избрать схему рис. 22.6. Если нелинейный элемент имеет преимущественно емкостный характер, т. е. в нем энергия электрического поля преобладает над энергией магнитного поля, что наблюдается, например, в неоновой лампе, работающей при сравнительно больших напряжениях и ничтожных токах, то следует избрать схему на рис. 22.7.

22.5. Общие соображения об устойчивости режима в сложных нелинейных электрических цепях, питаемых от источников постоянного напряжения

В общем случае для сложной цепи, включенной под действие постоянного напряжения и содержащей нелинейные сопротивления с падающими участками характеристик, а также содержащей в отдельных ветвях индуктивные катушки, конденсаторы и резисторы с постоянными параметрами, для анализа устойчивости значений постоянных токов, которые являются частными решениями уравнений, описывающих систему, необходимо пользоваться тем же методом, который был применен при рассмотрении приведенных в предыдущих параграфах примеров.

Составив по законам Кирхгофа систему уравнений для рассматриваемой нелинейной цепи и решив ее, например, с помощью методов, изложенных в главе 20, находим значения постоянных токов в цепи, отвечающие состоянию равновесия, и динамические сопротивления нелинейных элементов при этих значе- ниях токов. Если все эти сопротивления положительны, то соответствующее

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

445

равновесие устойчиво. Если же хотя бы одно динамическое сопротивление отрицательно, то надлежит исследовать вопрос об устойчивости соответствующего состояния.

Давая малое приращение ? току в одном из нелинейных элементов, находим, пользуясь системой уравнений цепи и найденными значениями динамических сопротивлений, приращения всех других токов и напряжений. При этом считаем, что динамические сопротивления нелинейных элементов остаются постоянными при малых отклонениях от рассматриваемого положения равновесия. Это соответствует тому первому приближению, которое было сделано в приведенных ранее примерах при отбрасывании членов с ? в степенях, больших, чем первая. По сути дела, применяя такой метод, мы линеаризуем характеристики нелинейных элементов вблизи точек равновесия. Такой метод, соответственно, иногда называют методом л и н е а р и з а ц и и в м а л о м.

Имея систему уравнений с получившими приращения токами и систему уравнений при равновесии и вычитая вторую из первой, получаем систему линейных уравнений для приращений токов или напряжений при указанном первом приближении. Решая эту систему относительно приращений ? отдельных токов, получим, вообще говоря, линейные уравнения n-го порядка.

Анализ переходных процессов вблизи точек равновесия для малых отклонений можно произвести всеми методами теории линейных цепей. Для этого достаточно в исходной цепи, содержащей в общем случае индуктивные катушки, конденсаторы и резисторы с нелинейными характеристиками, заменить эти нелинейные элементы линейными, параметры которых равны дифференциальным параметрам Lä, Cä, rä. Если в исходной цепи имеются элементы с линейными характеристиками, то они вносятся в расчетную схему без изменений, так как для них дифференциальные и статические параметры тождественны.

При таком подходе получаем возможность непосредственно для приращений формировать систему уравнений. Характеристические уравнения, соответствующие им, имеют ï корней k, и решения при отсутствии кратных корней имеют вид

kn

??0k e kt .

k 1

Корни k могут быть все вещественны или могут иметь в своем составе также пары сопряженных комплексных корней. В последнем случае происходят колебательные процессы.

С интересующей нас точки зрения важно следующее: если вещественные части всех корней характеристических уравнений отрицательны, то ? 0 ïðè t , процесс оказывается затухающим и рассматриваемое состояние равновесия устойчивое.

Если хоть один корень имеет положительную вещественную часть, то ? нарастает с увеличением t è состояние равновесия неустойчивое.

Если система уравнений сформирована относительно переменных состояния, то анализ устойчивости может быть произведен и без отыскания корней характеристического уравнения.

446 Часть 3. Теория нелинейных электрических и магнитных цепей

Пусть относительно приращений токов в индуктивных катушках и напряжений на зажимах конденсаторов (переменных состояния) получена система уравнений в виде

d

uC

A

uC

ïðè

uC

uC

(0)

,

dt

i L

i L

i L

t 0

i L (0)

ãäå A — матрица, составленная из дифференциальных параметров элементов цепи согласно топологическим особенностям цепи. Заметим, что переходный процесс для малых приращений происходит только за счет энергии магнитных полей индуктивных катушек и энергии электрических полей конденсаторов, и поэтому в обобщенных ветвях остаются только пассивные элементы. Для коэффициентов характеристического уравнения

a0 pn a1 pn 1 a2 pn 2 an 1 p an 0

имеем ak (–1)k Ν — главные миноры k-го порядка.

Принимая во внимание критерий Рауса—Гурвица (см. § 14.8), для выяснения устойчивости процесса достаточно исследовать условия

a 8 0; a 8 0;			a1	a0		8 0;	a1	a0	0	8 0 è ò. ä.
							a	a a
0	1		a3	a2			3	2	1
							a5	a4	a3

В качестве примера рассмотрим цепь, представленную на рис. 22.8, à, состоящую в общем случае только из нелинейных элементов. Эквивалентная схема этой цепи для малых приращений при условии U0 const представлена на рис. 22.8, á, а граф схемы — на рис. 22.8, â. Из графа для сечения по ветви 2 дерева имеем i2 i3 i; для контура, образованного связью 4, имеем u1 u4 u.

Ðèñ. 22.8

Для токов, определяемых сечением 1, и напряжений, определяемых контуром, образованным связью 3, имеем систему уравнений:

C

du1

u1

i

èëè

du

1

u

1

i;

ä

3

dt

r

dt

r

C

C

ä

ä4

ä4

ä

L

di3

u

r

i

èëè

di

1

u

rä2

i.

ä dt

1

ä2

3

dt

Lä

Lä

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

447

В матричной форме

1

1

d

u

rä4Cä

Cä

u

A

u

.

dt

i

1

rä2

i

i

Lä

Lä

Главный минор порядка 0 равен единице. Главный минор первого порядка равен сумме диагональных элементов с обратным знаком. Главный минор второго порядка в данном случае есть определитель матрицы À. Таким образом, имеем

1

rä2

1

rä2

rä2

1

a 1; a ( 1)1

;

a

.

0

1

rä4Cä

Lä

rä4Cä

Lä

2

rä4 LäCä

LäCä

Условиями устойчивости точки равновесия будут

1

rä2

1

8 0

è

rä2

1

8

0.

ä Lä

LäC

rä4C

ä rä4

Приведенная ранее методика исследования устойчивости точки равновесия для сложных цепей требует большого объема вычислений. Так, например, число главных миноров k-го порядка для матрицы À порядка (ï ï) равно Cnk n!/k!(ï – k)!. Суммарное число операций для вычисления коэффициен-

òîâ àk характеристического уравнения матриц высокого порядка может оказаться слишком большим даже для современных ЭВМ. Поэтому данную методику целесообразно применять для относительно простых цепей.

А. М. Ляпунов доказал, что указанное выше первое приближение, приводящее к линейности уравнений для малых отклонений от положения равновесия, вполне достаточно, чтобы по отмеченным критериям судить об устойчивости состояния. Особым является случай при нулевых значениях вещественной части корней, когда надо учитывать члены с ? в более высокой степени, чем первая.

Если бы система уравнений оставалась линейной при любых сколь угодно больших ?, то в случае неустойчивого состояния раз возникшее отклонение ? возрастало бы до бесконечности. В действительности замена участков характеристик нелинейных элементов вблизи точек равновесия отрезками прямых допустима только при малых отклонениях ? от положения равновесия. При больших ? надо учитывать нелинейность характеристик. Это может привести к ограничению получающихся отклонений, т. е. к переходу системы в новые устойчивые состояния. Так, в рассмотренном в § 22.2 примере положительное отклонение тока от точки À неустойчивого равновесия переводит систему в точ- ку Â устойчивого равновесия, причем это связано именно с нелинейностью характеристики u F (i).

Особый интерес такие соображения имеют в отношении колебательных систем. Здесь выход системы из состояния неустойчивого равновесия приводит к возникновению колебаний с нарастающей амплитудой. Однако вследствие нелинейности характеристик элементов цепи нарастание амплитуды колебаний может оказаться ограниченным, и наступает устойчивый периодический процесс.

Ðèñ. 22.9

448 Часть 3. Теория нелинейных электрических и магнитных цепей

Такой процесс называют а в т о к о л е б а т е л ь н ы м, так как цепь питается от источника постоянного напряжения и колебания возникают внутри самой цепи вследствие ее особых свойств. Теория устойчивости периодических движений детально разработана А. М. Ляпуновым. Мы рассмотрим этот вопрос на примерах транзисторного генератора и генератора релаксационных колебаний.

22.6. Возбуждение автоколебаний в нелинейной системе с обратной связью. Транзисторный генератор

В предыдущих параграфах мы видели, что при питании электрической цепи от источника постоянного напряжения могут возникнуть неустойчивые состояния равновесия. Возникшие вследствие случайного толчка небольшие отклонения от такого состояния равновесия в дальнейшем нарастают. Особый интерес представляют колебательные системы, в которых возникшие отклонения от положения неустойчивого равновесия развиваются в виде колебательного процесса. Как уже было сказано, амплитуда этих колебаний ограничивается вследствие нелинейных свойств цепи. В § 22.2, 22.3 и 22.4 были рассмотрены случаи, когда причиной неустойчивого состояния являлось наличие в цепи нелинейного элемента с падающей характеристикой.

В § 13.7 отмечалась возможность возникновения неустойчивых состояний вследствие наличия достаточно большой положительной обратной связи.

Характерным примером этого последнего случая является транзисторный генератор. Простейшая схема такого генератора, построенная с использованием полевого транзистора (см. § 19.11), изображена на рис. 22.9.

Мы рассмотрим условия самовозбуждения колебаний в этой конкретной схеме именно с целью выявления роли обратной связи на основе общих положений об устойчивости, сформулированных в предыдущем параграфе, а также на основе общих зависимостей, характеризующих цепи с обратными связями.

Обратная связь в рассматриваемой схеме генератора осуществляется с помощью взаимной индукции между колебательным контуром L, C и цепью затвора полевого транзистора. Раз возникшие вследствие начального толчка колебания в конту-

ðå L, Ñ создают переменное напряжение на затворе, поддерживающее эти колебания.

Выясним требования к значению коэффициента взаимной индукции Ì, при которых обеспечивается достаточная для самовозбуждения колебаний положительная обратная связь. Составим уравнения цепи. Напряжение на контуре u связано с током в ветви r, L контура уравнением

u ri L dtdi . Напряжение uñè между стоком и истоком равно

uñè U 0 u U 0 ri L dtdi .

Ðèñ. 22.10

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

449

Напряжение uçè между затвором и истоком равно ЭДС взаимной индукции: uçè M dtdi , так как током затвора, а соответственно, и падением напряжения от него в цепи затвора пренебрегаем.

Ток в цепи стока равен сумме тока i в катушке контура и тока i1 C dudt :

i		i i i C	du	i rC	di	CL	d 2 i	.
	ñ
		1	dt		dt		dt2

Òîê ic транзистора нелинейно зависит от напряжения uñè между стоком и ис-

током и от напряжения uçè между затвором и истоком. Эту зависимость можно

записать в общем виде: iñ !(uçè ,uñè ).

При постоянном напряжении U0 в цепи и отсутствии колебаний в контуре через триод будет протекать постоянный ток iñ0. Так как постоянный ток не проходит через конденсатор, то ток iñ0 проходит через катушку L и, следовательно, iñ0 i0. Постоянный ток i0 не индуцирует ЭДС в цепи затвора, и uçè 0. На контуре имеется малое постоянное напряжение u0 ri0, а на стоке транзистора постоянное напряжение uñ0 U0 – u0. Это состояние равновесия на рис. 22.10 изображено точкой À на семействе характеристик триода.

Пусть в результате случайного толчка ток в катушке получил небольшое приращение ? и принял значение i i0 + ?. Соответственно, все величины получат приращения, определяемые вышеприведенными уравнениями цепи, а именно:

u r? L

d ?

;

u

r? L

d ?

;

u

M

d ?

; i

? rC

d ?

LC

d 2 ?

.

dt

ñè

dt

çè

dt

ñ

dt

dt2

Нелинейное уравнение ic ! (uçè, uñè) дает связь между величинами iñ, uçè

è uñè. Воспользуемся разложением функции iñ ! (uçè, uñè) в ряд по степеням

малых величин uçè è uñè. Имеем

i

i

Ηi

ñ

u

Ηi

ñ

u

1 Η 2 i

ñ

( u

)2

1 Η 2 i

ñ

( u

)2

c

ñ0

Ηuçè

çè

Ηuc

cè

çè

cè

2 Ηuçè2

2 Ηucè2

Пренебрегая малыми величинами второго и более высоких порядков, получаем

i

i

i

Ηic

u

Ηic

u

S u

+ G u

.

ñ

ñ

ñ0

çè

cè

çè

cè

Ηu

Ηucè

çè

Здесь S — крутизна характеристики в точке равновесия A è G 1/Râí, причем G — выходная проводимость триода, а Râí — его внутреннее сопротивление.

Пренебрежение малыми величинами второго и более высоких порядков соответствует линеаризации характеристики вблизи точки равновесия. Иными словами, мы полагаем, что величины S è G постоянны в пределах малого отклонения тока iñ от точки равновесия.

450 Часть 3. Теория нелинейных электрических и магнитных цепей

Подставляя в последнее уравнение величины iñ, uçè è uñè, выраженные че- рез ?, получим

? rC

d ?

LC

d 2

?

SM

d ?

Gr? GL

d ?

,

dt

dt

2

dt

dt

èëè

d 2 ?

2−

d ?

2

? 0, ãäå

2−

rC SM GL

;

2

1 Gr

.

dt2

dt

0

LC

0

LC

Характеристическое уравнение 2 2−

2 0 имеет корни

0

1ϑ

2

− j

2 − 2 − j.

0

Они будут сопряженными комплексными, когда − < 0. При этом процесс будет колебательным с частотой . Решение уравнения для ? имеет вид

2

? ?0k e kt ?01e 1t ?02 e 2t Ae−t sin( t ).

k 1

Величина ?01 + ?02 A sin является начальным отклонением тока i от его значения i0.

Колебания будут затухающими и состояние равновесия устойчивым около значения тока i0, если вещественные части корней характеристического уравнения отрицательны, т. е. − > 0.

Состояние будет неустойчивым и раз возникшие колебания будут нарастать, если вещественные части корней характеристического уравнения положительны, т. е. − < 0. Последнее и явится условием самовозбуждения колебаний. Имеем это условие в виде

SM GL rC 9 0, ò. å. M 9 GL rC . S

Таким образом, для положительности обратной связи необходимо, чтобы M было отрицательно, и для обеспечения самовозбуждения абсолютное его значе- ние должно удовлетворять условию

M 8 GL rC . S

Эти колебания нарастали бы беспредельно, если бы прямолинейная часть характеристики простиралась в обе стороны до бесконечности. В действительности характеристика триода нелинейна, и это имеет решающее значение для установления устойчивых колебаний с вполне определенной амплитудой. Что это будет в действительности так, вытекает из простых физических соображений. Возрастание колебательной составляющей тока от точки A по характеристике вверх ограничено током насыщения триода, а вниз — невозможностью изменения направления тока через него. Вопрос об установлении устойчивой амплитуды количественно будет рассмотрен в § 22.15.

Для пояснения процессов в транзисторном генераторе на рис. 22.11 приведена векторная диаграмма для основных гармоник колебательных составляющих

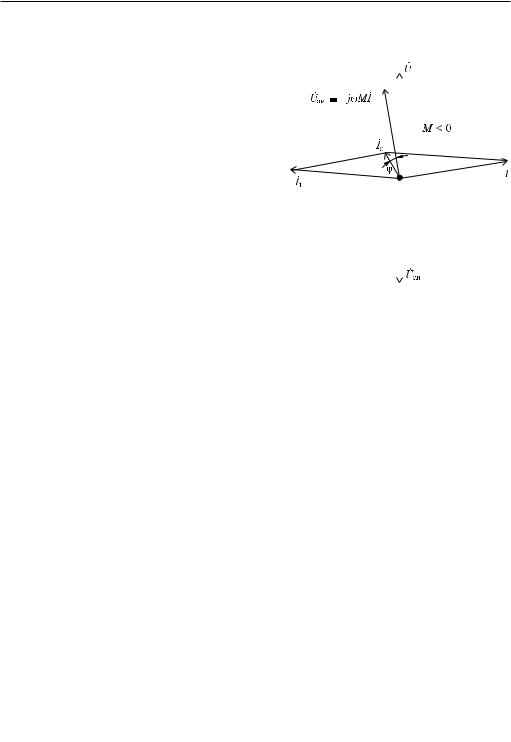
Глава 22. Элементы теории колебаний и методы расчета переходных процессов 451

токов и напряжений. Ток в катушке I отстает от напряжения на контуре U на угол, меньший #/2, но близкий к #/2 вследствие высокой добротности конту-

ра. Ток в конденсаторе I1 упреждает напря-
жение U на угол #/2, поскольку потерями
в конденсаторе пренебрегаем. Напряжение
на затворе U	j MI опережает ток I
çè
íà óãîë #Θ2, òàê êàê Ì < 0. Напряжение на
стоке U ñè равно и противоположно напря-
жению на контуре, так как для переменных
составляющих имеем U		ñè	– U. Сумма то-
ков в катушке I и в конденсаторе I1 равня-
åòñÿ òîêó I ñ .
Из диаграммы хорошо видно, что пере-
менная составляющая		напряжения U ñè íà
стоке находится почти в противофазе с на-
пряжением на затворе. При этом, посколь-
ку сдвиг фаз ! междуU è I ñ близок к нулю,				Ðèñ. 22.11

мощность UI	cos ! 8 Ι и энергия поступает в контур. Сдвиг фаз между током I
ñ			ñ
и напряжением U		ñè	равен # – !. Поэтому

U ñè I ñ cos(# !) UI ñ cos !9 0,

и транзистор работает в режиме генератора колебаний.

Обычно на практике режим, в котором работает транзисторный генератор, отличается от рассмотренного тем, что напряжение на затворе имеет также постоянную составляющую. Этим достигается повышение коэффициента полезного действия генератора, так как работа происходит на нижнем участке характеристики триода и в моменты больших значений uñè òîê iñ стока практически равен нулю, что и приводит к снижению потерь в триоде. Переменная составляющая тока iñ при этом существенно отличается от синусоидальной, ток же i в контуре остается практически синусоидальным вследствие большой добротности контура.

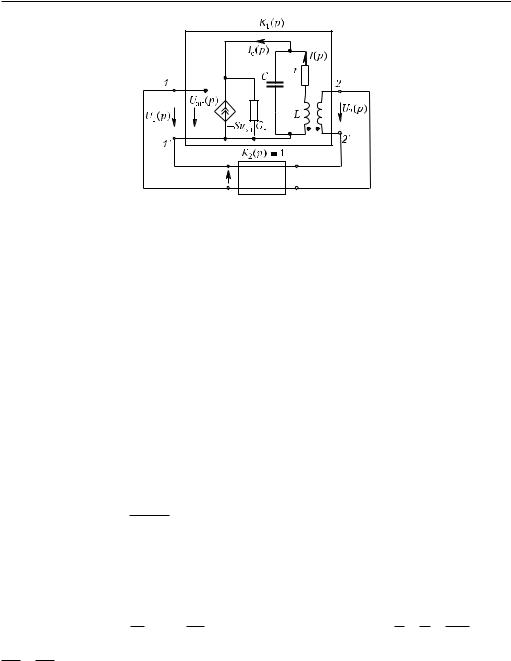
Рассмотрим вопрос об условиях возбуждения автоколебаний в транзисторном генераторе (см. рис. 22.9), пользуясь эквивалентной схемой и понятием о передаточной функции замкнутой и разомкнутой систем.

Рассматривая процесс на малом участке характеристики, который принимается линейным, получаем линейные уравнения; следовательно, можем воспользоваться операторным методом. На рис. 22.12 изображена схема генератора, в которой полевой триод заменен его эквивалентной схемой.

По схеме рис. 22.12 легко рассчитать передаточную функцию всей замкнутой системы, если известны передаточные функции K1(p) è K2(p) разомкнутой системы и устройства обратной связи. Согласно изложенному в § 13.7, при наличии обратной связи для передаточной функции замкнутой системы имеем

K(p)	U 2 (p)					K1(p)			.
	U	çè	(p)		1	K (p)K		(p)
						1	2

20 являются теми же самыми, что были получены раньше.

452 Часть 3. Теория нелинейных электрических и магнитных цепей

Ðèñ. 22.12

В данном случае K2(p) 1, a K1(p) рассчитываем, полагая обратную связь от-

сутствующей. Операторное изображениеU (p) напряжения на разомкнутых вы-

2

ходных зажимах равно

1

(r pL)

I

(p)

pC

c

r pL

1

U

(p) pMI(p) pM

U(p)

pC

pM.

2

r pL

r pL

Учитывая, что I c

(p)

SU

çè

( p)(1 rCp+ LCp2

)

получим

LCp2 + (rC+GL) p+ rG + 1

(p)

U

(p)

SMp

K

2

1

U çè

(p)

p2 LC p(rC

GL) rG 1

и окончательно

K(p) U 2 (p) U çè (p)

SMp

1

.

r

SM

2

G

1

1

Gr

LC

p

p

L

C

LC

LC

Знаменатель K(ð), приравненный к нулю, дает характеристическое уравнение дифференциального уравнения для напряжения uçè на затворе триода. Оно является одновременно также характеристическим уравнением для ?,

поскольку uçè M dtdi M ddt?. Содержащиеся в нем члены Lr GC SMLC 2− è

LC1 LCGr

Генераторы колебаний можно построить также на основе операционных усилителей, охваченных обратной связью.

Найдем условие самовозбуждения колебаний генератора, схема которого изображена на рис. 22.13, пользуясь понятиями передаточных функций замкнутой и разомкнутой систем.