книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Глава 22. Элементы теории колебаний и методы расчета переходных процессов 473

Исследуем этим методом разряд конденсатора на цепь, состоящую из катушки с ферромагнитным сердечником и участка с сопротивлением. Пусть емкость конденсатора Ñ 1 мкФ и сопротивление цепи, включая и сопротивление обмотки катушки, r 200 Ом. Возьмем катушку, рассмотренную в § 22.9 (см. рис. 22.18), и, пренебрегая явлением гистерезиса, будем считать, что кривая намагничивания как при возрастании, так и при убывании тока изображается кривой 1 íà ðèñ. 22.17.

Дифференциальное уравнение цепи имеет вид

d <

ri

1 t

i dt u

(0) 0

C

dt

C

0

èëè

d 2 <

r

di

1

i

0.

dt2

dt

C

В данном случае удобнее принять в качестве координаты x на фазовой плоскости значение потокосцепления <. Соответственно, уравнение можно перепи-

ñàòü â âèäå					d <
	d 2 <	r	di				1 i			< 0.
	dt2		d <		dt		C <

Величины d</di Lä è </i Lñò — динамическая и статическая индуктивности, являющиеся функциями <, определяемыми из кривой намагничивания.

Полагая < x è d</dt y, запишем уравнение в форме
	r		1		dy		r		1
y		y		x 0 èëè				y		x .
	Lä		CLñò		dt		Lä		CLñò

Разделив последнее уравнение на dx/dt y, получим уравнение фазовой тра-

ектории				r		1
					y		x
	dy			Lä		CLñò			.
	dx				y
Полагая dy/dx k, находим уравнение изоклины
	y				x				,
			CLñò (k r Lä )

ãäå Lñò F1(x) è Lä F2(x).

Задаваясь рядом значений x <, вычисляем из последнего уравнения y и по точкам строим изоклину для данного k. На рис. 22.35 построены изоклины для данной конкретной задачи, около изоклин помечены соответствующие им зна- чения угла arctg k наклона касательных к фазовой траектории. Под этим углом нанесены черточки, пересекающие изоклину, и по ним проведена фазовая траектория для начальных значений UC (0) 680 Â è <(0) 0. По характеру фазовой траектории видно, что разряд имеет колебательный характер.

Для построения кривой <(t) необходимо определить моменты времени, соответствующие точкам фазовой траектории. Промежуток времени t, в течение

Ðèñ. 22.36

474 Часть 3. Теория нелинейных электрических и магнитных цепей

	которого совершается переход от Α-й точки (xΑ, yΑ) фазовой траектории к близ-
	êîé ê íåé (Α + 1)-й точке (xΑ ., yΑ .), можно приближенно определить следующим
		dx		xΑ 1	1		1
	образом. Так как y		, òî t			dx. Обозначая		f(x), имеем по теореме
		dt		xΑ	y		y

о среднем t f(Ψ) xΑ . – xΑ f(Ψ) x, ãäå xΑ < Ψ < xΑ+1. При небольшом интерва-

ëå t и монотонном изменении y в этом интервале можно принять f(Ψ) 1 ,

yñð

ãäå yñð yΑ yΑ 1 . При этом имеем 2

t x .

yñð

Если рассматриваемый участок фазовой траектории является отрезком прямой

с тангенсом угла наклона к оси абсцисс

dy

k

yΑ 1 yΑ

, òî dt

dx

dy

1 dy

dx

xΑ 1 xΑ

dy y

k y

и, следовательно,

yΑ 1

1 dy

1

yΑ 1

t

ln

.

yΑ

k y

k

yΑ

Если рассматриваемый участок фазовой траектории является дугой окружности, имеющей центр на оси абсцисс, то t вычисляется следующим образом. Выразим координаты точек этой дуги окружности в виде õ Rcos! + x0, y Rsin!, ãäå x0 — координата центра окружности, R — радиус окружности и ! — угол между осью абсцисс и направлением радиуса, проведенного в точку (x, y) дуги. Получаем

	xΑ 1		dx	!Α 1
	t			d! !,
			y
	x	Α		!
				Α

ãäå ! — центральный угол рассматриваемой дуги.

В случае, если отрезок фазовой траектории близко совпадает с отрезком пря-

мой, то приближенно можно воспользоваться формулой t 1ln yΑ 1 , за исклю- k yΑ

чением случаев, когда yΑ 0 èëè yΑ+1 0, а также когда yΑ+1 yΑ. В последнем слу- чае хороший результат дает формула t x/yñð.

Если отрезок фазовой траектории близко совпадает с дугой окружности, имеющей центр на оси абсцисс, то приближенно можно воспользоваться формулой t !. В частности, этой формулой рекомендуется пользоваться для случаев, когда yΑ 0 èëè yΑ+1 0 (рис. 22.36). Заметим, что в этом последнем случае величины t, вычислен-

ные по формулам t x/yñð è t !, отличаются меньше чем на 1 % при ! 20Τ.

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

475

Вычисляя промежутки времени, соответствующие последовательным отрезкам фазовой траектории, легко построить кривую <(t), что и сделано на рис. 22.37. На этом же рисунке построена кривая i(t), причем значения тока брались из кривой намагничивания (см. рис. 22.17) по соответствующим значениям потокосцепления <.

Ðèñ. 22.37

Рассмотренное в настоящем и предыдущем параграфах изображение переходных процессов на фазовой плоскости дает возможность наглядно обозреть весь характер этих процессов. Этот метод применим в случаях, когда процесс описывается уравнениями первого или второго порядка со свободным членом, не зависящим от времени. Особенно ценным является то, что здесь открываются новые возможности расчета переходных процессов в нелинейных цепях.

22.15. Метод медленно меняющихся амплитуд — метод Ван-дер-Поля

Во многих нелинейных колебательных электрических цепях при установившемся режиме изменение во времени тока в колебательном контуре весьма близко к синусоидальному. Это означает, что в уравнении члены, содержащие нелинейные коэффициенты, малы по сравнению с остальными членами. В таких случаях может быть применен так называемый м е т о д м е д л е н н о м е н я ю щ и х с я

476 Часть 3. Теория нелинейных электрических и магнитных цепей

а м п л и т у д, называемый также методом Ван-дер-Поля. Далее этот метод будет изложен на примере анализа тока в колебательном контуре лампового генератора и напряжения на сетке лампы, пропорционального производной от этого тока во времени (рис. 22.38).

Нетрудно убедиться в том, что уравнение для тока в колебательном контуре имеет вид, аналогичный полученному в § 22.6 уравнению для тока в контуре транзисторного генератора

Ðèñ. 22.38

d 2 i

2−

di

2 i

I

0

SDU

0

,

dt2

dt

LC

0

ãäå 2− S

M DL

r

è 2

1 rSD

, S — крутизна характеристики, D — ïðî-

LC

L

0

LC

ницаемость лампы (см. § 19.8), I0 , U0 — величины, определяющие состояние лампы при отсутствии колебаний.

Учитывая, что rSD << 1 вследствие применения в генераторах контуров с вы-

сокой добротностью, примем 2

1 (LC). Нам будет удобнее рассматривать на-

0

di

пряжение u

на сетке лампы, равное u

M

. Дифференцируя уравнение для i

c

c

dt

и умножая на (–M), получим

d 2uñ

2−

duñ

2u

0.

(*)

ñ

dt2

dt

0

Нелинейным является член 2− dudtñ , так как наклон характеристики S зависит от uc и, следовательно, 2− dudtñ f (uñ , dudtñ ). В ламповом генераторе этот член мал

по сравнению с остальными членами, что вытекает из рассмотренных в § 22.6 условий возбуждения колебаний в ламповом генераторе. Вместе с тем этот член хотя и является малым, оказывает определяющее влияние на процесс возбуждения колебаний и на процесс нарастания и установления амплитуды колебаний.

Ïðè − 0 имели бы место незатухающие синусоидальные колебания. Наличие малого нелинейного члена 2− dudtñ приводит к тому, что и установив-

шиеся колебания будут немного отличаться от синусоиды. В процессе установления амплитуда A нарастает. Обычно скорость изменения амплитуды A и начальной фазы настолько мала, что dA/dt << A 0 è d /dt << 0, т. е. за период T 2#/ 0 изменение A амплитуды составляет малую долю самой амплитуды A и изменениеначальной фазы много меньше 2#. Величину uc при этом можно записать в виде

Ðèñ. 22.39

uñ A(t)cos[ 0 t (t)] Acos( 0 t ).

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

477

Здесь как A A(t), òàê è (t) являются медленно меняющимися во времени величинами. При этих условиях кривая A(t) определяет собой огибающую кривой uc(t) (ðèñ. 22.39).

Скорость изменения напряжения uc на сетке равна

du

ñ

dA

d

cos(

t

) A

sin(

t )

A

sin(

t ).

0

0

0

0

0

dt

dt

dt

Последнее приближение соответствует тому, что мы принимаем условие

dA

cos(

t

) A

d

sin(

t

) 0.

(**)

dt

0

0

dt

Приняв такое условие, получаем

d 2uñ

d

[

Asin(

t

)]

dA

sin(

t

)

dt2

dt

0

0

0

dt

0

2 Acos(

t

)

A

d

cos(

t

).

0

0

0

0

dt

Подставляя в уравнение (*) значение d 2 uc /dt 2 è uc и замечая, что главные члены 0A cos ( 0t + ) сокращаются, получаем уравнение для остающихся малых величин:

dA

sin(

t

) A

d

cos(

t

)

2− du

ñ

1

du

ñ

f u

,

.

(***)

0

0

0 dt

0

dt

dt

ñ

dt

Заметим, что сделанные нами приближения вносят определенную неточность в значения этих малых величин. В этом непосредственно можно убедиться, если составить величину d 2 uc /dt 2, взяв производную от полного выражения duc /dt. Однако эти малые величины незначительно изменяют величины uc, duc /dt è

d 2 u	c	/dt 2, и, следовательно, определенный таким образом процесс будет близок
к истинному.

Из уравнений (**) и (***) определяются отдельно скорости изменения ам-

плитуды и фазы. Умножаем эти уравнения, соответственно, на sin ( 0t +

) è íà

cos ( 0t + ); затем, складывая или вычитая полученные уравнения, находим

dA

1

du

ñ

0

f uñ ,

sin( 0 t

);

2

dt

0

dt

2

(****)

d

1

duñ

1

2

f u ,

cos(

0

t

).

2

A 0

dt

ñ

dt

3

Усредняя правую часть в интервале от t äî t + T, мы вправе считать в пределах этого интервала величины A и неизменяющимися и равными их значениям в момент t. Действительно, было сказано, что эти величины мало меняются в тече- ние любого периода. В результате такого усреднения получим

1 1			t T				du	ñ
			f u			,			sin( 0 t )dt Μ(A);
T 0					ñ
			t				dt

Ðèñ. 22.40

Ðèñ. 22.41

478 Часть 3. Теория нелинейных электрических и магнитных цепей

1 1			t T				du	ñ
			f u			,			cos( 0 t )dt <(A).
T A 0					ñ
			t				dt

При выполнении операции интегрирования в соответствии со сказанным будем считать величины A и постоянными, но в выражениях Μ(A) è <(A) âåëè- ÷èíà A является функцией времени, равной своему значению в момент t в нача- ле интервала усреднения.

В результате уравнения (****) после усреднения их правых частей приобре-

òàþò âèä

dAdt Μ(A) è ddt <(A).

Решая эти уравнения, находим законы изменения во времени медленно меняющихся амплитуды и начальной фазы. Амплитуда в установившемся режиме определяется из условия, что dA/dt Μ(A) 0.

Изображая процесс на фазовой плоскости (uc, duc/dt), получим в установившемся режиме замкнутый предельный цикл. Можно показать, что этот установившийся режим и соответствующий ему цикл являются устойчивыми, если dΜ(A)/dA < 0 при значении A, соответствующем этому циклу, и неустойчивыми, если dΜ(A)/dA > 0 при этом значении A.

Применим эти общие соображения к уравнению (*) лампового генератора. Пусть характеристика лампы ià f(uc) может быть аппроксимирована зависимостью

ià auñ3 buñ c,

причем коэффициенты a, b è c подобраны так, что вся кривая имеет вид, представленный на рис. 22.40, т. е.

a –S0/(3U 2s ), b S0 è c ias/2, ãäå S0 — наклон

c

характеристики при uc 0. Такая аппроксимация обеспечивает достаточно точное аналитическое выражение действительной характеристики лампы только в пределах –Ucs uc Ucs. Наклон характеристики в любой ее точке в этих пределах получается равным

	di	à					u2
S			3au2	b S		1		ñ	.
								2
	duñ		ñ		0		U
								ñs

Таким образом, малый нелинейный член уравнения имеет вид

du

ñ

2−

du

ñ

M

DL

f u

,

S

ñ

dt

dt

)

LC

(

ãäå

M DL

r

m S

0

;

LC

L

		r du			ñ	(nuc2 m)	du	ñ
			,						,
				dt
		L +					dt

n S0 M DL . U 2s LC

c

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

479

Отметим, что n > 0 è m > 0 из условия самовозбуждения − < 0.

Теперь, учитывая что мы приняли закон изменения напряжения на сетке

â âèäå uc A cos ( 0t + ) è duc/dt – A 0 sin ( 0t + ), ãäå A è — медленно меняющиеся величины, получаем

1

1

t T

duñ

Μ(A)

(nu2 m)

sin(

t

)dt

T

c

dt

0

0

t

T

t T

1

1

[nA2 cos2 (

t

) m][

Asin(

t )]

0

0

0

0

t

sin( 0 t

m

n

3

A

n

2

)dt

A

A

m

A

.

2

8

4

2

Таким образом, уравнение для медленно меняющейся амплитуды имеет вид

dA		A		n			2
			m			A		.
dt		2		4

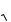
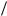Состояния равновесия имåþò место при A const èëè ïðè dA/dt 0, ò. å. ïðè A A1 0 è ïðè A A2 2mn.

Первое значение амплитуды A1 0 соответствует отсутствию колебаний. Это состояние неустойчиво. Действительно, при появлении вследствие случайного

толчка колебаний даже с любой малой амплитудой A0 0 получаем dA/dt > 0,
	n			2						0
òàê êàê m > 0 è m			A	0		8 0	при малом A	. Соответствующая точка u
	4						0		c

è duc /dt 0 (начало координат) на фазовой плоскости является неустойчивым фокусом (рис. 22.41). Нарастание амплитуды возникших колебаний будет происходить до тех пор, пока снова величина dA/dt не станет равной нулю. Это бу-

äåò ïðè A A		n			2
	, когда m			A	2		0. Легко заметить, что такое состояние являет-
2		4

ся устойчивым, так как при A < A2 имеем dA/dt > 0 и амплитуда возрастает, а при A > A2 будет dA/dt < 0 и амплитуда убывает. Соответствующий предельный цикл на фазовой плоскости будет устойчивым, т. е. при любых отклонениях от этого цикла фазовые траектории свертываются к нему (см. рис. 22.41).

Подставляя в формулу для A2 выражения для m è n, получаем соотношение, связывающее амплитуду установившихся колебаний с параметрами характеристики лампы и колебательного контура:

A2 2U cs

1

rC

2U cs

1

rC

.

S

0 (M DL)

S

0

M DL

dA

A

n

2

Уравнение

m

A

позволяет определить не только установившую-

dt

2

4

ся амплитуду колебаний, но и весь переходный процесс от начального толчка A A0 ïðè t 0 до установления амплитуды A2. Подстановкой x A–2 приведем это уравнение к виду dx/dt + mx0 n/4. Решение этого уравнения имеет вид

480 Часть 3. Теория нелинейных электрических и магнитных цепей

x

n

ce mt

1

ce mt

èëè A

A2

.

4m

A22

1

cA

2 e mt

2

Произвольную постоянную c определим из условия, что A A0 ïðè t 0. Получаем c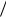 (1A02 1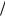A22 ).

Åñëè m < 0, ò. å. åñëè − > 0, то условия самовозбуждения не обеспечены и при случайном возникновении малых колебаний с амплитудой A 0 получаем dA/dt < 0. Следовательно, раз возникшие колебания затухают. При этом на фазовой плоскости точка в начале координат является устойчивым фокусом.

22.16. Частотные свойства нелинейных цепей

В линейных электрических цепях в кривой тока возможны только те гармоники, которые содержатся в кривой ЭДС. В отличие от этого в нелинейной цепи в кривой тока появляются гармоники, не содержащиеся в кривой ЭДС.

Пусть ток и напряжение на зажимах нелинейной цепи в некоторых пределах их изменения связаны соотношением

i au bu2 .

Предположим, что u U1m sin 1t + U2m sin 2t, причем 2 è 1 вообще не кратны друг другу. Подставим это выражение для u в формулу для i и заменим квадраты синусов выражениями через косинусы двойных углов, а произведение синусов — через косинусы разности и суммы углов. Тогда увидим, что в выражении для тока i, кроме постоянной составляющей и составляющих с частотами 1 è 2, появляются также составляющие с удвоенными частотами 2 1, 2 2 и составляющие с к о м б и н а ц и о н н ы м и ч а с т о т а м и 1 – 2 è 1 + 2, ò. å.

i

b

(U 2

U 2

) aU

sin t aU

sin

t

b

U 2

cos2 t

2

1m

2m

1m

1

2m

2

2

1m

1

b

U 2

cos2

t bU

U

cos(

)t bU

U

cos(

)t.

2

2m

2

1m 2m

1

2

1m

2m

1

2

Уже на этом простом примере наглядно видны особенности частотных свойств нелинейных цепей. Во-первых, среднее значение (постоянная составляющая) тока i зависит от амплитуды гармонических составляющих напряжения. Несмотря на то что кривая напряжения не содержит постоянной составляющей, в кривой тока в данном случае возникает постоянная составляющая, что является результатом несимметрии характеристики. Во-вторых, в кривой тока появляются гармоники с частотами более высокого порядка (2 1, 2 2,1 + 2) по сравнению с гармониками в кривой напряжения. В-третьих, в кривой тока возникают гармоники с комбинационными частотами ( 1 – 2 è 1 + 2). Таким образом, в кривой тока появляется ряд новых гармоник с частотами, отличными от частоты гармоник в кривой напряжения. Это обстоятельство и дает возможность использовать нелинейные цепи для преобразования частоты, для модуляции и детектирования колебаний, что было рассмотрено ранее.

Если отношение 1 ê 2 представляет собой рациональное число, то напряжение u есть периодическая функция. Если при этом 1/ 2 n/m, то период напря-

Глава 22. Элементы теории колебаний и методы расчета переходных процессов

481

жения u будет равен nT1 mT2. Åñëè 1 > 2 è 1 – 2 имеет период, превышающий nT1, то период тока окажется больше периода напряжения, что можно рассматривать как возникновение в кривой тока гармоник с частотой, меньшей частоты напряжения. Эти гармоники называют с у б г а р м о н и к а м и.

Применяя приведенные рассуждения для нелинейных элементов, характеристики которых могут быть аппроксимированы полиномами более высоких порядков, придем к выводу, что в нелинейных цепях с подобными элементами возможны колебания, частоты которых заполняют широкий диапазон рациональных чисел.

Комбинационные колебания, в частности субгармоники, могут возникать и при действии на зажимах нелинейной цепи синусоидального напряжения, т. е. напряжения одной частоты. При этом напряжения на отдельных участках цепи с нелинейными элементами будут несинусоидальными, т. е. состоять из нескольких синусоидальных составляющих разных частот. Согласно вышеизложенному, в этом случае при надлежащих условиях могут возникать комбинационные колебания.

22.17. Значение нелинейных электрических цепей в современной технике

Все изложенное в настоящей части показывает исключительно широкие возможности, которые открываются при использовании нелинейных элементов для создания электрических цепей, обладающих самыми различными весьма важными для практики свойствами.

Мы видели, что, используя нелинейные элементы, можно осуществить стабилизаторы напряжения и тока, усилители мощности, модуляторы, генераторы незатухающих колебаний, выпрямители, инверторы и т. д. Рассмотренными примерами далеко не исчерпывается перечень возможных применений нелинейных элементов в электрических цепях. Так, например, очень важным является создание устройств для формирования импульсов напряжения различной формы, создание так называемых спусковых устройств — триггеров, в которых используется неустойчивое состояние и при плавном изменении входного напряжения происходит скачок напряжения или тока на выходе, создание на этой основе счетчиков импульсов и т. д.

Радиотехника, автоматика, телемеханика, электроизмерительная техника, техника электронных быстродействующих счетно-решающих и управляющих машин, электроэнергетика и другие области техники на современном этапе развития все шире используют особые свойства нелинейных цепей. Еще большие возможности открываются в этом направлении в будущем.

Вместе с тем явления в нелинейных системах представляют собой еще недостаточно разработанную и весьма интересную область для теоретических и экспериментальных исследований, хотя многое, как отмечалось, здесь уже сделано; причем весьма существенный вклад в решение нелинейных задач внесли русские ученые.

Вопросы, задачи и упражнения к главам 19–22

19.1. Параметры элементов нелинейных электрических цепей

ВОПРОСЫ И УПРАЖНЕНИЯ

1.(О) Может ли ток в нелинейной электрической цепи содержать постоянную составляющую, если в ней действуют только периодические ЭДС?

2.При каком условии динамическое и дифференциальное сопротивления (проводимости) нелинейного элемента одинаковы?

3.(О) Справедливы ли соотношения: à) rñò 0; á) rä 0; â) rñò > 0; ã) rä > 0; ä) rñò < 0; å) rä < 0 для точек 0, À, Â, Ñ, D (рис. В19.1) характеристики нелинейно-

го элемента?

4. (О) Для каких точек (0, À, Â, Ñ, D) изображенной на рис. В19.1 характеристики нелинейного элемента справедливы соотношения: à) rä > rñò; á) rä rñò; â) rä < rñò?

5. Вид экспериментально полученной вольт-амперной ха-
рактеристики нелинейного элемента зависит от частоты
приложенного напряжения. Можно ли в этом случае утвер-	Ðèñ. Â19.1
ждать, что нелинейный элемент является инерционным?

6.Какие (большие или малые) значения динамических сопротивления rä и проводимости gä присущи нелинейным элементам, применяемым для стабилизации тока и напряжения, в области стабилизации?

7.(Р) Каким следует принять сопро-

тивление резистора r в изображенной на рис. В19.2, à схеме для стабилизации напряжения u2 10 Â ïðè r2 100 Îì, u1 20 B? Вольт-амперная характери-

стика нелинейного элемента изображена Ðèñ. Â19.2 íà ðèñ. Â19.2, á.

8. (Р) В каком диапазоне изменения входного напряжения u1 (в условиях предыдущего упражнения) напряжение u2 на нагрузке остается неизменным? В каком диапазоне изменения сопротивления нагрузки r2 напряжение на ней сохраняется постоянным?

19.2. Транзистор как элемент электрической цепи

ВОПРОСЫ И УПРАЖНЕНИЯ

1.(О) Почему у биполярных транзисторов в схеме с общим эммитером коэффициент усиления по току меньше, чем у полевых?

2.(О) Какие основные допущения использованы при получении эквивалентных схем для малосигнального режима работы триода?

3.Почему входное сопротивление полевых транзисторов значительно больше входного сопротивления биполярных транзисторов?