Метод прогонки

Метод застосовується для розв’язування СЛАР, основна матриця яких має три діагональний вигляд:

(1)

Розширена матриця системи (1) :

Перше і останнє рівняння системи (1) містять по 2 невідомих. Їх можна розглядувати як крайові умови.

необхідно знайти розв’язок системи (1) методом виключення Гауса.

Якщо до (1) застосувати алгоритм прямого хода Гауса, то замість , отримаємо, яка має три діагональний вигляд:

Звідси формула зворотнього ходу:

(2)

Формули для прогоночних коефіцієнтів визначаються, якщо записати (2) дляі підставити в (1):

(3)

Це формули прямого ходу.

Зворотній хід методу прогонки починається з обчислення , для чого використовується останнє рівняння (2) і (1). Звідки:

(4)

Інші значення невідомих визначаються по (2) .

Методика розв’язування задачі:

Прямий хід.

1. Обчислюється .

2. Обчислюють прогоночні коефіцієнти по формулам (3).

Зворотній хід.

3. Визначається .

4. За формулами (2) знаходять .

Зауваження.

1. Даний метод називається методом скалярної прогонки, тому що при розв’язуванні задачі на кожному і-тому кроці визначається скалярна величина .

2. Аналогічний підхід використовується для розв’язування СЛАР з п’ятидіагональними матрицями.

3. Алгоритм методу прогонки коректний, якщо для всіх маємо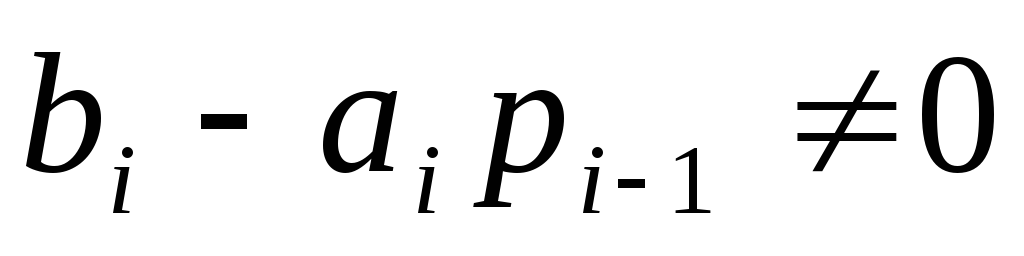, істійкий, якщо .

4. Достатньою умовою коректності і стійкості прогонки є умова переваги діагональних елементів в матриці для:

(5)

і має сувору нерівність хоча б при одному і.

5. Алгоритм методу є досить економічним і потребує для своєї реалізації кількість операцій пропорційно п.

Приклад 1. розв’язати СЛАР методом прогонки:

Дана система задовольняє умові коректності і стійкості прогонки .

Розширена матриця систем

Прямий хід. Обчислимо прогоночні коефіцієнти:

Зворотній хід:

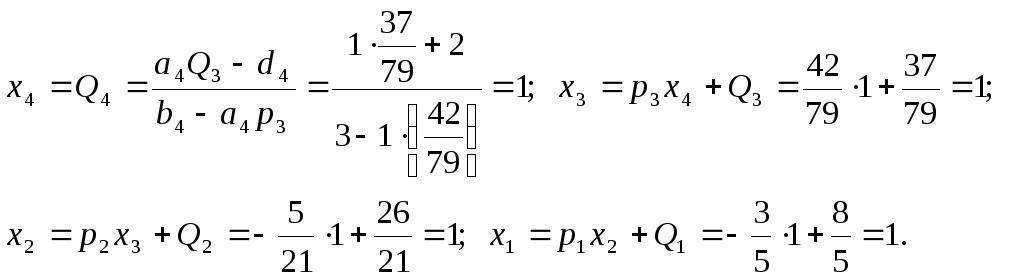
Відповідь: .

Приклад 2. Розв’язати СЛАР методом прогонки

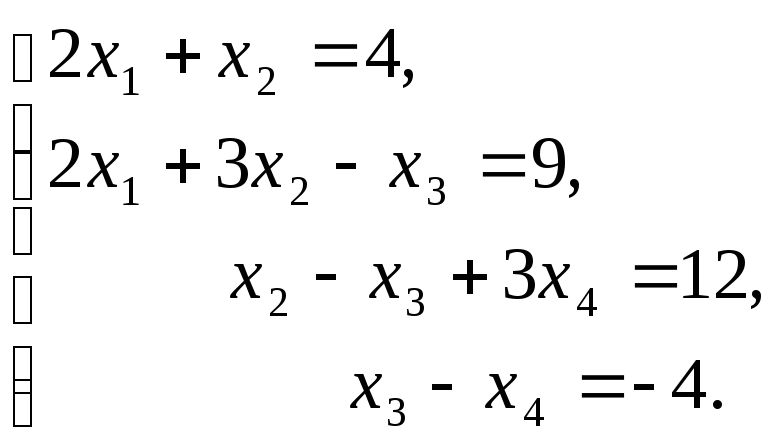
СЛАР не задовольняє умовам коректності і стійкості прогонки.

Прямий хід.

Зворотній хід.

Відповідь:

Чисельне диференціювання

Постановка задачі чисельного диференціювання

Нехай на відрізку на нерівномірній або рівномірній сітцізадані:

• сіткова функція ;

• точки , у яких необхідно знайти значення похідних;

• бажаний порядок точності (апроксимації) відносно.

• Необхідно із заданим порядком точності (апроксимації) обчислити значення похіднихв точкахсітки, дер – порядок похідної, а , де, яка не залежить від.

Методика отримання формул чисельного диференціювання

Для отримання формул чисельного диференціювання заміняють вихідну функцію на відрізкуінтерполюючою функцією, як правило, поліноміальною. Тоді похіднана. Якщо при цьому відома похідна, то похибка похідної, тобто похибка похідної вихідної функції дорівнює похідній від похибки цієї функції.

Чисельне диференціювання – менш точна операція, ніж інтерполяція, тому що, наприклад, близькість ординат двох кривих іна відрізкуне гарантує малого розходження похідних.

Формули чисельного диференціювання на основі першої інтерполяційної формули Ньютона

Нехай задана у рівновіддалених вузлахвідрізказа допомогою значень. На цьому відрізку функціюзаміняють інтерполяційним поліномом Ньютона:

,

де

Так як , то

(1)

(2)

Оцінка похибки

(3)

Приклад 1. Знайти функції, яка задана таблично:

50	1,6990	0,0414	-0,0036	0,0005
55	1,7404	0,0378	-0,0031
60	1,7782	0,0347
65	1,8129

. З точністю до різниць 3 порядку:

. Точне значення

Приклад 2. Шлях, який пройдено прямолінійно рухомою точкою надається у таблиці

	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
	0,000	1,519	6,031	13,397	23,396	35,721	50,000	65,798	82,635	100
	1,519	4,512	7,366	9,999	12,325	14,279	15,798	16,837	17,365
	2,993	2,854	2,633	2,326	1,954	1,519	1,039	0,528
	-0,139	-0,221	-0,307	-0,372	-0,435	-0,480	-0,511
	-0,082	-0,086	-0,065	-0,063	-0,045	-0,031
	-0,004	0,021	0,002	0,018	0,014

Недолік формул (1) і (2) у тому, що вони використовують лише односторонні значення функцій при . Відносно більшу степінь точності мають симетричні формули диференціювання, які враховують значення даної функції як при, так і при.

Приклад 3. З використанням таблиці значень з крокомзнайтиів точці.

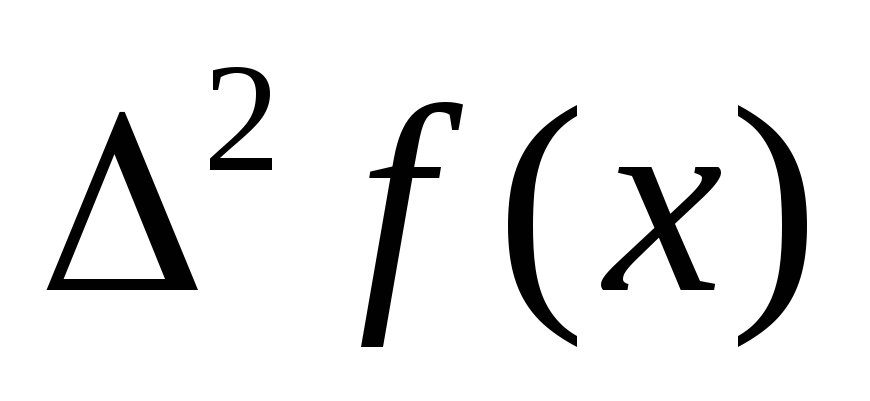
0,00	0,00000	0,10017	0,00100	0,00101	0,00003
0,05	0,10017	0,10117	0,00201	0,00104	0,00003
0,10	0,20134	0,10318	0,00305	0,00107
0,15	0,30452	0,10623	0,00412
0,20	0,41075	0,11035
0,25	0,52110