Зведення лінійної системи алгебраїчних рівнянь до вигляду, який є зручним для ітерації

Нехай маємо СЛАР:

(1)

Якщо , то помножимо (1) зліва на матрицю, де- матриця з малими за модулем коефіцієнтами.

Тоді , або

(2)

де .

На практиці із заданої системи виділяють рівняння з коефіцієнтами, модулі більше суми модулів коефіцієнтів рівняння. Кожне виявлене рівняння записують так у рядок нової системи, щоб найбільший за модулем коефіцієнт був діагональний.

З останніх невикористаних і виділених рівнянь системи складають лінійні комбінації лінійно незалежні між собою так, щоб був виконаний указаний вище принцип компенсування нової системи і усі вільні рядки були заповнені.

Приклад 1. Звести систему до вигляду, який був би зручним для застосування метода ітерацій.

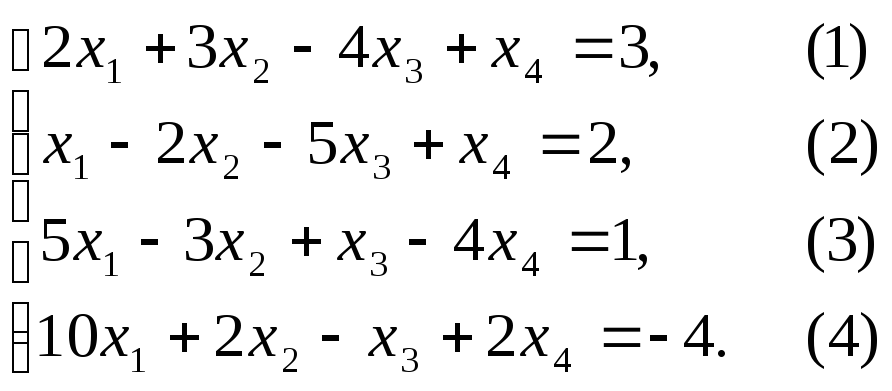
(4) – без змін

(1) – (2)

(2) – без змін

Розв’язуючи її відносно діагональних елементів:

Приклад 2. Записати систему у вигляді, придатному для застосування методу ітерацій.

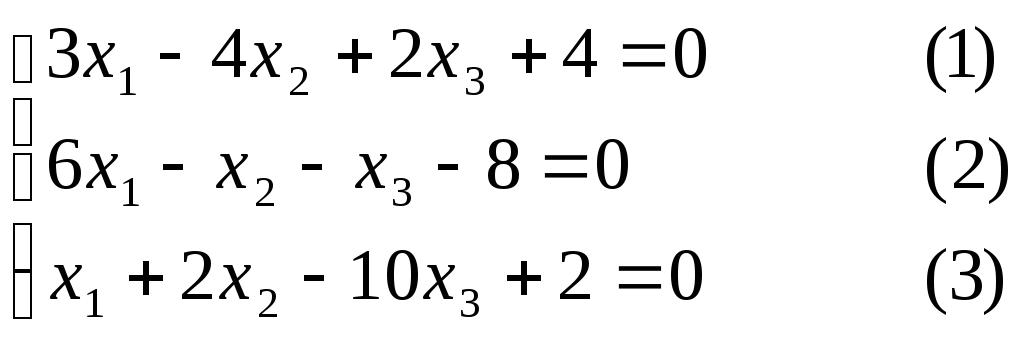
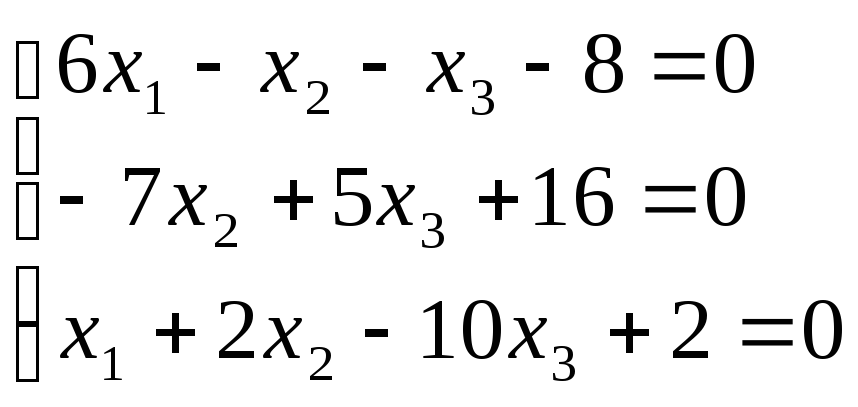
(2) без змін

(3) без змін

Звідси

Метод Зейделя

Метод Зейделя є модифікацією простої ітерації. Він полягає у тому, що для обчислення наближення невідомого, привикористовують уже обчислені ранішенаближення невідомих.

Нехай дана зведена лінійна система:

(1)

Виберемо початкове наближення коренів .

Нехай -е наближення кореніввідоме. Тоді відповідно до методу Зейделя будуємонаближення за формулами:

(2)

Усі умови збіжності для методу простої ітерації вірні і для методу Зейделя. У матричному вигляді

(3)

де івідповідно нижня та верхня трикутні матриці:

Теорема 1. Ітераційний процес (3) збігається за будь-якого початкового наближення тоді і тільки тоді, коли усі корені рівняннябудуть за модулем менші від одиниці, тобто.

Загалом метод Зейделя збігається до розв’язку СЛАР швидше, ніж метод ітерацій, але приводить до більш об’ємних обчислень. Метод Зейделя може бути збіжним навіть у тому випадку, коли процес простої ітерації розбіжний. Можливі випадки, коли процес ітерації за методом Зейделя збігається повільніше простої ітерації й навіть розбіжний за методом Зейделя.

Приклад 1. За методом Зейделя розв’язати систему рівнянь:

Запишемо систему у зведеному вигляді

Нульове наближення .

Результати наближень за методом Зейделя

0	1,2	0	0
1	1,2	1,06	0,948
2	0,9992	1,0054	0,9991
3	0,9996	1,0002	1,0000
4	1,0	1,0	1,0
5	1,0	1,0	1,0

Точне значення

Приклад 2. Методом Зейделя з точністю знайти невідомі СЛАР для початкового наближення:

.

Так як для, то похибка не перевищує.

Відповідь: .

Приклад 3. Методом Зейделя розв’язати систему. Порівняти з методом простої ітерації.

Метод релаксації

Нехай маємо СЛАР:

(1)

Перенесемо вільні члени (1) ліворуч і розділимо на: І рівняння на , ІІ – натощо. Тоді отримаємо систему, яка підготовлена до релаксації:

де (2)

Нехай - початкове наближення (2). Підставивши ці значення в (2), отримаємо нев’язки:

(3)

Якщо дати приріст, то відповідна нев’язказменшиться на, а всі інші нев’язкизбільшаться на величину. Щоб обернути в нуль чергову нев’язку, треба величинідати приріст. Тодііпри.

Метод релаксації (встановлення, ослаблення) у простішій формі полягає в тому, що на кожному кроці обертають в нуль максимальну за модулем нев’язку шляхом зміни значення відповідної компоненти наближення. Процес закінчується, коли всі нев’язки останньої перетвореної системи будуть дорівнювати нулю із заданою точністю.

Приклад. Методом релаксації розв’язати систему, обчислюючи з точністю до .

(1)

(2)

Запишемо (1) у вигляді, придатному для релаксації (2). Виберемо початкове наближення і знайдемо відповідні нев’язкиТоді:

(3)

За загальною теорією виберемо Тоді:,

Аналогічно попередньому: тощо.

	0	0	0	0,93	0	0	0,07	0	0	1,00
	0,60	0,76	0,93	0	0,04	0,07	0	0	0
	0	0	0,86	0	0	0,13	0	0	0,01	1,00
	0,70	0,86	0	0,09	0,13	0	0,01	0,01	0
	0	0,8	0	0	0,18	0	0	0,02	0	1,00
	0,80	0	0,09	0,18	0	0,01	0,02	0	0