Метод Зейделя

Деяка модифікація методу простої ітерації. Основна ідея в тому, що при обчисленні -го наближення невідомоївраховуються уже обчислені ранішенаближення невідомих, тобто виконуютьсяпослідовні ітерації.

Схема методу Зейделя для системи (2):

Умова закінчення ітерацій .

Вказана вище теорема збірностей для простих ітерацій залишається вірною для ітерацій за методом Зейделя.

Цей метод має кращу збіжність, ніж метод простих ітерацій, але приводить до більш об’ємних обчислень. Процес Зейделя може бути збіжним навіть у тому випадку, коли процес ітерацій розбіжний. Можливі випадки, коли метод Зейделя збігається і повільніше процесу ітерації, і навіть розбіжний по Зейделю.

Приклад. Знайти корені системи

які розташовані у І квадранті методом Зейделя з точністю 0,001.

Перетворення системи до вигляду зручного для ітерацій, та пошук початкового наближення приведені вище.

Отримані результати:

.

При цьому:

Метод Ньютона

Розглянемо систему рівнянь (1), і нехай (х) мають непе­рервні похідні першого порядку. Нехай також відоме -те набли­ження хкоренях*.

Тоді (1) можна переписати у вигляді

f(х+х)= 0, де ∆х = х^*– х.

Для визначення похибки ∆х розкладемо функцію f(х) в ряд Тейлора й обмежимося першими диференціалами, тобто лінеаризуємо функцію:

Врахуємо (3.1) і перейдемо до векторного вигляду запису:

де J(x) – матриця Якобі (якобіан) системи (3.1):

Звідси випливає спосіб обчислення чергового (+ 1)-го набли­ження:

хx(J(x))f(x); (3.6)

У достатньо малому околі розв'язку х* ітераційний процес (3.6) є збіжним, якщо існує обернена матриця J (х), а для цього необхідно, щоб

Зауваження 1. Ітераційний процес (3.5) має квадратичну швидкість збіжності. Якщо початкове наближення х⁽⁰⁾ вибране вдало, то процес (3.6) дає задовільну точність за три-п'ять ітерацій.

Зауваження 2. Якщо на всіх ітераціях використовувати за­мість J(х) стале, обчислене для х⁽⁰⁾ значення якобіану J(х⁽⁰⁾), то отримаємо модифікований метод Ньютона:

Швидкість збіжності у цьому випадку стане лінійною і, відпо­відно, збільшиться кількість необхідних для досягнення заданої точності ітерацій.

Розглянемо метод Ньютона для системи двох рівнянь.

Запишемо систему (3.1) у вигляді

(3.7)

Тоді згідно з методом Ньютона послідовні наближення обчис­лимо за формулами

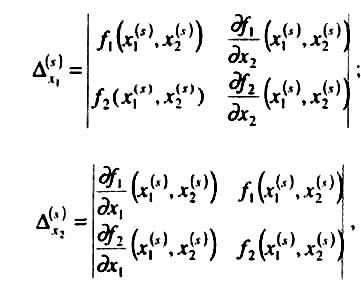
а матриця Якобі має вигляд

Початкові наближення можна визначити, наприклад, графічно.

Метод Ньютона ефективний лише тоді, коли вектор початко­вих наближень х⁽⁰⁾ достатньо близький до розв'язку системи (3.1) х*.

Приклад 1. Перевірити чи ітераційний процес буде збіжний для системи не­лінійних рівнянь

Розв'язування. Графічно можна знайти грубе наближення значення коренів Обчислимо якобіан

Якобіан відмінний від нуля, тому ітераційний процес збіжний.

Приклад 2. Методом Ньютона знайти розв’язок системи

який знаходиться у І квадранті з точністю .

Початкове наближення .

–матриця Якобі.

.

.

Цей самий результат можна отримати, якщо застосувати формулу (5):

Так як , то шукаємо друге наближення:

Звідки:

;

.

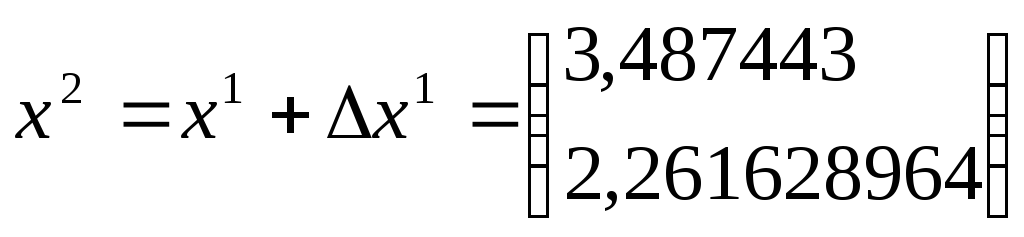Висновок: за методом простих ітерацій точність досягається за 4 ітерації, а за методом Ньютона – за 3.

Приклад 3. Знайти розв’язок системи методом Ньютона з точністю .

Початкові наближення .

Матриця Якобі:

.

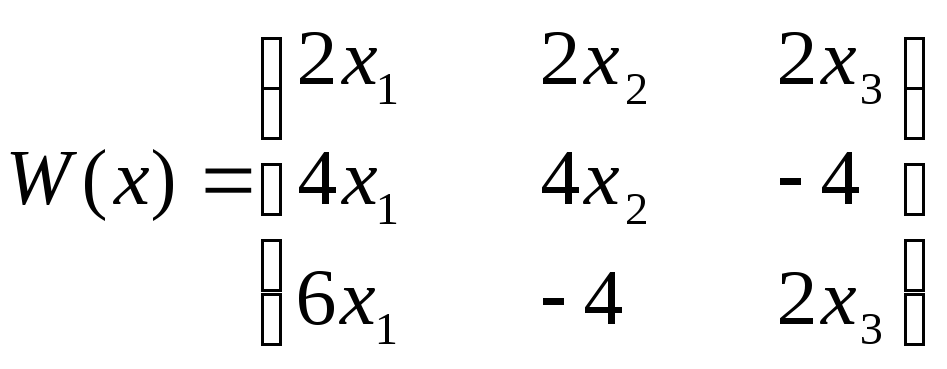В точці

.

Так як , то знаходимо:

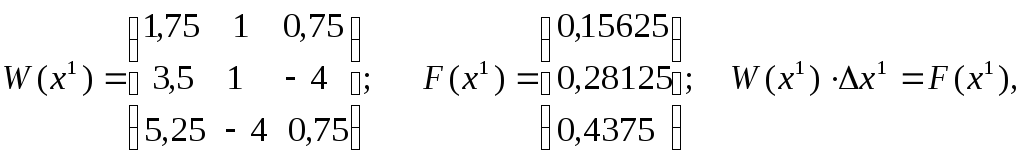звідси:

<