Модифікований метод Ньютона

У цьому методі обернена матриця шукається тільки один раз у початковій точці :.

Збіжність спрощеного методу Ньютона в загальному випадку гірше, ніж метод Ньютона.

Приклад 1. Знайти додатний розв’язок системи спрощеним методом Ньютона з точністю.

На малюнку видно, що для знаходження початкового наближення можна взяти .

; ;;;

Так як , то знаходимо:

Так як , то знаходимо три наближення:

Так як , то знаходимо чотири наближення:

Так як , то процес закінчений.

Розв’язування систем лінійних рівнянь (слар)

Способи розв’язування СЛАР в основному розподіляються на дві групи:

• точні методи (правило Крамера – історично перший метод, потребує арифметичних дій, метод Гауса – потребуєарифметичних дій, якіпри) тощо. Для сумісних СЛАР метод Гауса один із найефективніших;

• ітераційні методи (метод ітерації, метод Зейделя, метод релаксації).

Метод ітерації

Нехай задана СЛАР:

(1)

або в матричному вигляді:

()

Розв’яжемо перше рівняння відносно , друге – відноснотощо. Отримаємо еквівалентну систему(2):

(2)

або в матричному вигляді:

().

Систему (2) розв’яжемо методом послідовних наближень. За нульове наближення беремо стовпчик вільних членів .

Далі наближення обчислюємо за формулою

, при (3)

Якщо послідовність наближень має границю, тобуде розв’язком системи (2). У розгорнутому вигляді:

(3’)

Інколи систему (1) зводять до (2) так, щоб коефіцієнти , тобто для рівняння, наприклад:записують у вигляді зручному для застосування метода ітерацій.

Метод ітерації, який визначається за формулами (3) або (), гарно збігається, якщо елементи матриці малі за абсолютною величиною, тобто для успішного застосування процесу ітерації модулі діагональних елементів порівняно з модулями над діагональних елементів (вільні члени при цьому ролі не грають).

Приклад 1. Розв’язати СЛАР методом ітерації:

(4)

Зводимо систему (4) до нормального вигляду 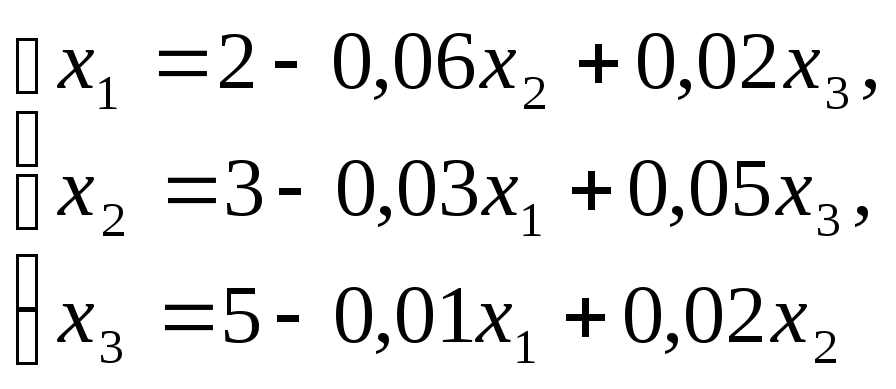(5):

(5)

У матричній формі (5) має вигляд:

()

За нульові наближення коренів системи (4) приймаємо . Підставляючи ці значення у праві частини (5) отримаємо перше наближення коренів:

Аналогічно друге наближення:

третє:

При застосуванні метода ітерацій немає необхідності за нульове наближення приймати стовпчик вільних членів. Збіжність процесу ітерації залежить тільки від властивостей матриці , причому при виконанні певних умов процес збігається при довільному початковому векторі. Збіжний процес має властивість само виправлятися, тобто окремі помилки в обчисленнях не відбиваються на кінцевому результаті, тому що помилкове наближення можна уявити собі, як новий початковий вектор.

Інколи обчислюють не самі наближення, а їх різниці:

Тоді

За нульове наближення приймають .

Тоді -е наближення:.

Тоді: 1) якщо , тоі;

2) якщо , тоі

Тоді .

Приклад 2. Розв’язати систему:

Запишемо систему у вигляді (2):

,

тощо.

Результати наведено у таблиці

Метод накопичення

0	-1,5	0,2	0
1	0,100	0,900	0,230
2	0,335	0,032	0,350
3	-0,159	-0,061	-0,021
4	-0,020	0,011	-0,008
5	0,010	0,009	0,006
6	0,002	-0,004	0,003
7	-0,004	0,000	-0,001
8	0,000	0,002	0,000
9	0,001	0,000	0,001
∑	-1,235	1,089	0,560

Тоді наближені значення коренів:

.

Недоліком цього методу ітерації є систематичне накопичення похибок при збільшенні числа доданків, у результаті чого виникають значні похибки шуканих коренів.

Теорема 1. Якщо для зведеної системи (2) виконано хоча б одну з умов:

, де ,, де, то процес ітерацій (3) збігається до єдиного розв’язку цієї системи, незалежно від вибору початкового наближення.

Наслідок. Для системи ,метод ітерації збігається, якщо виконані нерівності, тобто, якщо модулі діагональних коефіцієнтів для кожного рівняння системи більше суми модулів усіх інших коефіцієнтів за винятком вільних членів.

Приклад 3.

Методом простої ітерації розв’язати систему:

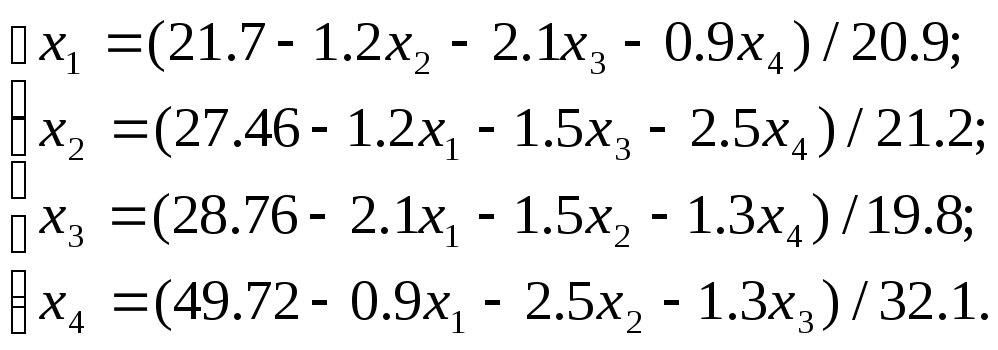
Коефіцієнти отриманої системи задовольняють умовам теореми:

Збіжність ітерацій гарантована. При цьому . Точність-го наближення.

У якості початкового наближення візьмемо елементи стовпчика вільних членів, округливши їх значення до двох знаків

;

Так як усі , то, причому похибка значень не перевищує.

Точні значення .

Приклад 4. Розв’язати систему, зробивши три ітерації. Указати похибку отриманого результату.

Умови збіжності виконані:

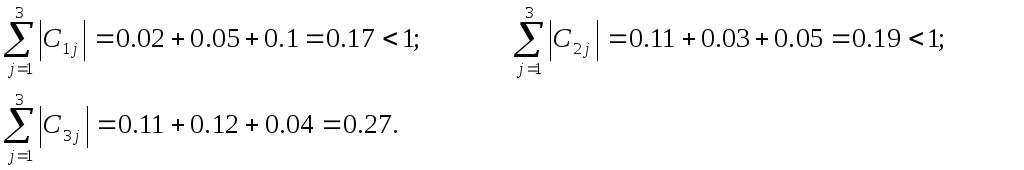
Початкове наближення: ;;

; .

Похибка:

Теорема 2. Для СЛАР ітераційний процес,збігається за будь-якого початкового наближеннятоді і тільки тоді, коли усі власні числа матриціВ за модулем менші від 1, тобто корені характеристичного рівняння були б за модулем менші, ніж одиниця