2.11. Дифференциальные уравнения

Дифференциальным уравнением называется уравнение, в которое неизвестная функция входит под знаком производной или дифференциала. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференци-

альным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется по-

рядком дифференциального уравнения.

Уравнение вида

		dy			( )
	F x , y ,			= 0
		dx

– дифференциальное уравнение первого порядка.

Вуравнении ( ) F – заданная непрерывная функция трех своих аргументов,

вчастности, она может не зависеть от х или у, но непременно должна содер-

жать dydx . Разрешая уравнение ( ) относительно dydx , будем иметь: dydx = f (x , y ).

Решением дифференциального уравнения называется всякая функция y =ϕ(x), которая при подстановке в уравнение обратит его в тождество.

Общая форма дифференциального уравнения n-го порядка имеет вид:

F (x, y, y ′, y ′′,..., y (n ) )= 0 .

Дифференциальное уравнение n-го порядка называется разрешенным от-

носительно старшей производной, если оно имеет вид y ( n ) = f (x, y, y ′,..., y ( n −1) ),

где f – некоторая функция от n+1 переменной.

Общим решением дифференциального уравнения n-го порядка называется такое его решение y =ϕ(x, C1 , C2 ,..., Cn ), которое является функцией переменной х

и n произвольных независимых постоянных С1, С2,…, Сn.

Частным решением называется решение, полученное из общего при некоторых конкретных числовых значениях постоянных С1, С2,…, Сn.

Общим решением дифференциального уравнения первого порядка y′ = f (x, y) в области D называется функция y =ϕ(x, C). Всякое решение y = ϕ (x, C 0 ), по-

лучающееся из общего решения y =ϕ(x, C) при конкретном значении С = С0 ,

называется частным решением.

Задача, в которой требуется найти частное решение уравнения y ′ = f (x, y ), удовлетворяющее начальному условию y(x0 )= y0 , называется задачей Коши.

Общему решению y =ϕ(x, C) на плоскости ХОУ соответствует семейство интегральных кривых, зависящее от одного параметра, а частному решению,

64

удовлетворяющему начальному условию y(x0 )= y0 , – кривая этого семейства, проходящая через заданную точку M 0 (x0 , y0 ).

	Если функция f (x, y) непрерывна и имеет непрерывную производную	∂ f	в
		∂ y

области D, то решение дифференциального уравнения y′ = f (x, y) при начальном условии y(x0 )= y0 существует и единственно, то есть через точку (x0 , y0 ) проходит единственная интегральная кривая данного уравнения (теорема Коши).

2.11.1. Методы интегрирования дифференциальных уравнений первого порядка

I. Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:

ddxϕ = f (x)g(y) или M (x)N(y)dx + P(x)Q(y)dy = 0 .

Если ни одна из функций f(x), g(y), M(x), N(y), P(x), Q(y) не равна тождественно нулю, то эти уравнения следует преобразовать к виду, в котором дифференциал и функции переменной х окажутся в одной части равенства, а переменной у – в другой. Для первой формы уравнения:

		dy		= f (x)dx ,
		g( y)
для второй формы					Q(y)
	M (x)
			dx	+		dy = 0 .
	P(x)				N(y)

Выполняя почленное интегрирование последних уравнений, получаем соотношения, которые определяют (чаще всего в неявной форме) решение исход-

ных уравнений:	∫ MP((xx))dx + ∫ QN((yy))dy = C .
∫ gdy(y)= ∫ f (x)dx + C ;

11.1. Два самых простых случая: когда g( y) =1или f (x) =1. В первом случае

имеем dy = f (x)dx и y = ∫ f (x)dx + C , а во втором				dy						dy
					= dx	и	∫				= x + C .
				g(y)					g(y)
Например, y′ = y . Получаем	x = ∫	dy	+ C = ln y − ln C = ln					y		. Используя свойст-
		y						C
во логарифма, получаем y = Ce x .

	11.2. Решить уравнение x(y 2 − 4)dx + y dy = 0 .	y dy
	∆ Разделив обе части уравнения на y 2 − 4 ≠ 0 , имеем x dx +		= 0 . Интег-
		y 2 − 4

рируя, находим x2 + ln y 2 − 4 = ln C или y 2 − 4 = Ce−x2 . Это общее решение данного уравнения.

65

11.3. Решить уравнение ln cos y dx + x tg y dy = 0 .

tg y dy

∆ Разделив обе части уравнения на

x ln cos y , имеем

dx

+

= 0 . Интег-

x

ln cos y

рируя,

находим

ln x + ∫

tg y dy

= ln x −

∫

d ln cos y

= ln x − ln ln cos y = ln C .

Откуда

ln cos y

ln cos y

x

= C

или x = C ln cos y . Мы получим общее решение данного уравнения в

ln cos y

виде функции x(y).

11.4. Решить уравнение y′ + sin(x + y)= sin(x − y).

∆ Используя тригонометрические формулы

sin(x + y)= sin x cos y + cos x sin y и

sin(x − y)= sin x cos y − cos x sin y ,

запишем уравнение в виде

y′ + sin x cos y + cos x sin y = sin x cos y − cos x sin y .

После сокращения в левой и правой частях уравнения sin x cos y

и переносе

cos x sin y в правую часть приведем уравнение к виду:

y′ = −2 cos x sin y или dy = −2 cos x sin y dx .

Разделяя переменные

dy

= −2 cos x dx , проинтегрируем обе части уравнения:

sin

y

∫

dy

= −2∫cos x dx + C

или ln

tg

y

= −2 sin x + C .

sin y

2

Это и есть общее решение исходного уравнения.

y

′

cos(x)

= ln y ,

удовлетворяющий

11.5. Найти частный интеграл уравнения y

начальному условию y(0)=1.

∆ Полагая y′ =

dy

, перепишем данное уравнение в виде cos x

dy

=

y

. Разде-

dx

dx

ln

y

ляя переменные,

получим

ln y

dy =

dx

. Интегрируя обе части,

будем иметь

y

cos x

ln y

dx

1

2

x

π

∫

dy = ∫

+ C

или

ln

y = ln tg

+

+ C .

Используя начальное условие

y

cos x

2

2

4

y =1 при x = 0 ,

находим C = 0 , так как ln1 = 0 . Окончательно получаем частное

решение

1

2

x

π

ln

y

= ln tg

+

.

2

2

4

Решить уравнения с разделяющимися переменными:

11.6. xy′ − y = y3

11.12. y′=ex+y +ex−y , y(0)=0

11.7. xyy′ =1 − x2

11.13.

dx

dy

y(1)=1

11.8. y − xy′ =1 + x2 y

+

= 0,

x(y −1)

y(x + 2)

11.9. xy dx + (x +1)dy = 0

′

π

11.14. y

+ cos(x + 2 y)= cos(x

− 2 y),

y(0)=

.

11.10. y′ + cos(x + y)= cos(x − y)

4

11.11.

yy

′

2x

= − cos y

66

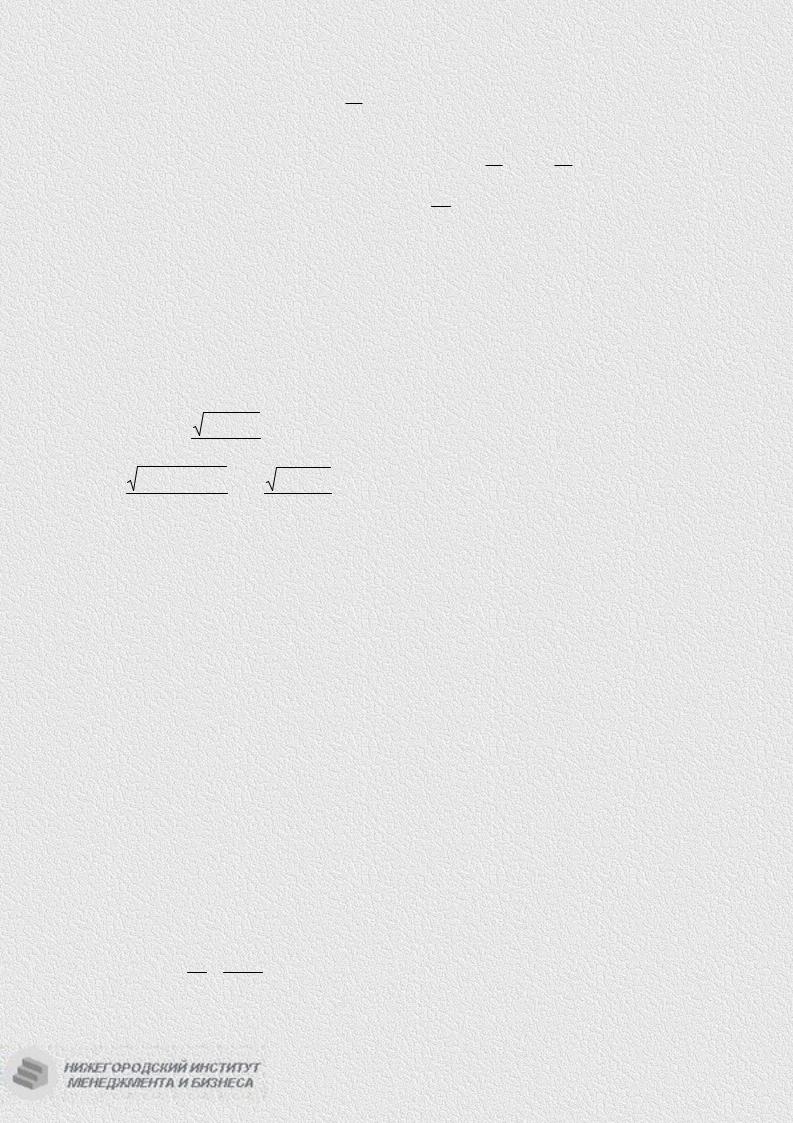
Замечание. Уравнение вида dydx = f (ax + by ), где a, b – постоянные, заменой z = ax + by приводится к уравнению с разделяющимися переменными относительно функции z(x). Дифференцируя z, имеем dxdz = a + b dydx . Тогда исходное

уравнение легко приводится к уравнению dxdz = a +b ×f (z), в котором перемен-

ные разделяются.

II. Однородные дифференциальные уравнения первого порядка

Функция f (x, y) называется однородной степени k, если для произвольного

числа λ выполняется равенство f (λx, λy)= λk f (x, y).
Например:
а)	f (x, y)= x 2 + 2xy		– однородная степени 2.
	(λx)2 + 2(λx)(λy)= λ2 (x 2 + 2 yx)
б)	f (x, y)=	x2 + y 2	– однородная степени 0.
		2x + 3y
	(λx)2 + (λy)2		x2 + y 2
	2(λx)+ 3(λy) = λ0		2x + 3y
в)	f (x, y)= x2 y 2 +1 – неоднородная.
	(λx)2 (λy)2 +1 ≠ x2 y 2 +1
Уравнение		вида	P(x, y)+ Q(x, y)= 0 называется однородным, если
P(x, y) и Q(x, y)		однородные функции первой степени.

Однородное уравнение может быть приведено к виду		y		. С помощью
	y′ = f
	x

подстановки u =	y	однородное уравнение приводится к уравнению с разделяю-
	x
щимися переменными по отношению к новой неизвестной u.
11.15. Найти общий интеграл уравнения (x2 − y 2 )dy − 2xy dx = 0 .
∆ Здесь P(x, y)= x2 − y 2 , Q(x, y)= −2xy . Обе функции – однородные второй
степени. Разделим уравнение на x2 и представим его в виде
			dy			2		y	.
								x
				=
			dx					y		2
				1 −
								x

	Введем			подстановку u =			y	,	откуда y = ux . Дифференцируя подстановку,
							x
		dy			du				dy
	имеем		= u + x			. Подставляя				в уравнение и делая замену в правой части,
		dx			dx				dx

получим u + x dudx = 1 −2uu 2 . Разделяя переменные и интегрируя, имеем:

dx		u 2 −1				dx		u 2 −1
	+		du = 0	;	∫		+ ∫		du = C .
x		u(u 2 +1)				x		u(u 2 +1)

67

Преобразуем второй интеграл:

ln

x

+ ∫

2

u

du − ∫

du

= ln C или ln

x

+ ln(u 2

+1)− ln

u

= ln C

u

2

+1

u

x(u 2 +1)= C u

Возвращаяськпрежнейнеизвестнойфункции, получаемокончательныйответ: x 2 + y 2 = Cy .

11.16. Найти интеграл уравнения y′ = x + 2 y . x

∆ Введем новую переменную y = ux . Проводя все вычисления, аналогичные

примеру 3.15, получим дифференциальное уравнение для u: x

du

=1+u .

dx

Разделяя переменные и интегрируя уравнение, получим y = cx2

− x .

11.17. Найти частное решение уравнения

y

y

y′ =

+sin

при начальном усло-

x

x

вии y(1)=

π

.

2

y

du

′

∆ Произведем подстановку x = u ,

откуда

y

= u + x dx . В результате получим

u + x

du

= u + sin u ; x

du

= sin u ;

du

=

dx

. Интегрируя,

имеем ln

u

= ln

x

+ ln C ,

tg

dx

dx

sin u

x

u

2

откуда

= arctg(Cx). Производя обратную замену,

находим общее решение ис-

2

ходного уравнения y = 2x arctg(Cx). Используя заданные начальные условия, по-

лучим

π

= 2 arctg C , откуда С=1.

Итак, искомое

частное решение имеет вид

2

y = 2x arctg x .

Решить однородные дифференциальные уравнения.

11.18.y′ = xy −1

11.19.(x2 + y 2 )dx − 2xy dy = 0

11.20.y dy + (x − 2 y)dx = 0

11.21.xy + y 2 = (2x2 + xy)y′

11.22.xyy′ = y 2 +2x 2

11.23.y′ = y + cos y

x x

11.24. xy′ = xe y x + y, y(1)= 0

III. Линейные дифференциальные уравнения первого порядка

Уравнение вида y′ + P(x)y = f (x) называется	линейным. Если	f (x)≠ 0 , то
уравнение называется линейным неоднородным,	а если Q(x)= 0	– линейным

однородным.

Общее решение линейного однородного уравнения y′ + P(x)y = 0 легко находится разделением переменных: dyy = −P(x)dx; ∫dyy = −∫P(x)dx; ln y = −∫P(x)dx + ln C

или, наконец, y = Ce −∫P(x)dx , где С – произвольная постоянная.

68

Общее решение линейного неоднородного уравнения можно найти тремя методами.

а) Метод Бернулли.

Будем искать решение в виде y = u(x)v(x), где u(x) и v(x) – две неизвестные функции. Так как y′ = u′v + v′u , то исходное уравнение преобразуется к виду

u′v + v′u + P(x)uv = f (x) или u[v′ + P(x)v]+ vu′ = f (x).

Одна из неизвестных функций может быть выбрана совершенно произвольно (поскольку лишь произведение uv должно удовлетворять исходному уравнению). Поэтому найдем сначала какое-либо частное решение v = v(x) уравнения

v′ + P(x)v = 0 ,						v = e−∫P(x )dx , обращающее в нуль коэффициент при u преобразо-
ванного уравнения. Тогда функция u = u(x)										– решение уравнения vu′ = f (x) или
u	′		f (x)		, откуда u = C + ∫ f (x)e		∫P(x)dx		dx .
		= v
		Общее решение исходного уравнения находится умножением v на u
						y = e		−∫P(x )dx ∫ f (x)e ∫P(x )dx + C .

б) Метод Лагранжа (метод вариации постоянной).

Сначала интегрируем однородное уравнение и считаем, что произвольная постоянная решения есть некоторая, подлежащая определению, дифференци-

( ) −∫P(x )dx

руемая функция от х. То есть считаем, что y = C x e . Найдем производную

	dy	=	dc		e−∫P(x )dx − C(x)P(x)e−∫P(x )dx и подставим ее в исходное неоднородное урав-
	dx
			dx
нение. Тогда получим:
				dc		e−∫P(x )dx − C(x)P(x)e−∫P(x )dx + f (x)C(x)e−∫P(x )dx = f (x) или		dC		= f (x)e∫P(x)dx .
								dx
				dx
		Откуда интегрируя,					получаем C(x)= ∫ f (x)e∫ P(x)dx dx + C2 .			Следовательно
	y = C(x)e−∫P[x]dx = C1e−∫P[x]dx						+ e−∫P[x]dx ∫ f (x)e∫P[x]dx dx . Первый член суммы – решение

однородного уравнения, второй член суммы – частное решение неоднородного уравнения.

в) Метод интегрирующего множителя.

У дифференциального уравнения первого порядка всегда есть интегрирующий множитель µ = e∫P(x )dx , который приводит уравнение к полному дифференциалу.

11.25. Найти общее решение уравнения y ′ −

2

y = 2 x 3 .

x

2

∆ а) Применим метод Бернулли. В нашем случае P (x )= −

, f (x )= 2 x 3 . Най-

дем функцию v(x), решая уравнение v ′ −

2

x

v = 0 .

Разделяя переменные, имеем

dv

2 dx

x

=

. После интегрирования получаем

ln v = 2 ln x

или

v = x2 . Уравнение

v

x

для функции u(x) имеет вид x 2

du

= 2 x 3 ,

du

= 2 x,

u = x 2

+ C .

Следовательно, об-

dx

dx

щее решение y = (x 2 + C)x2 = Cx 2 + x4 .

69