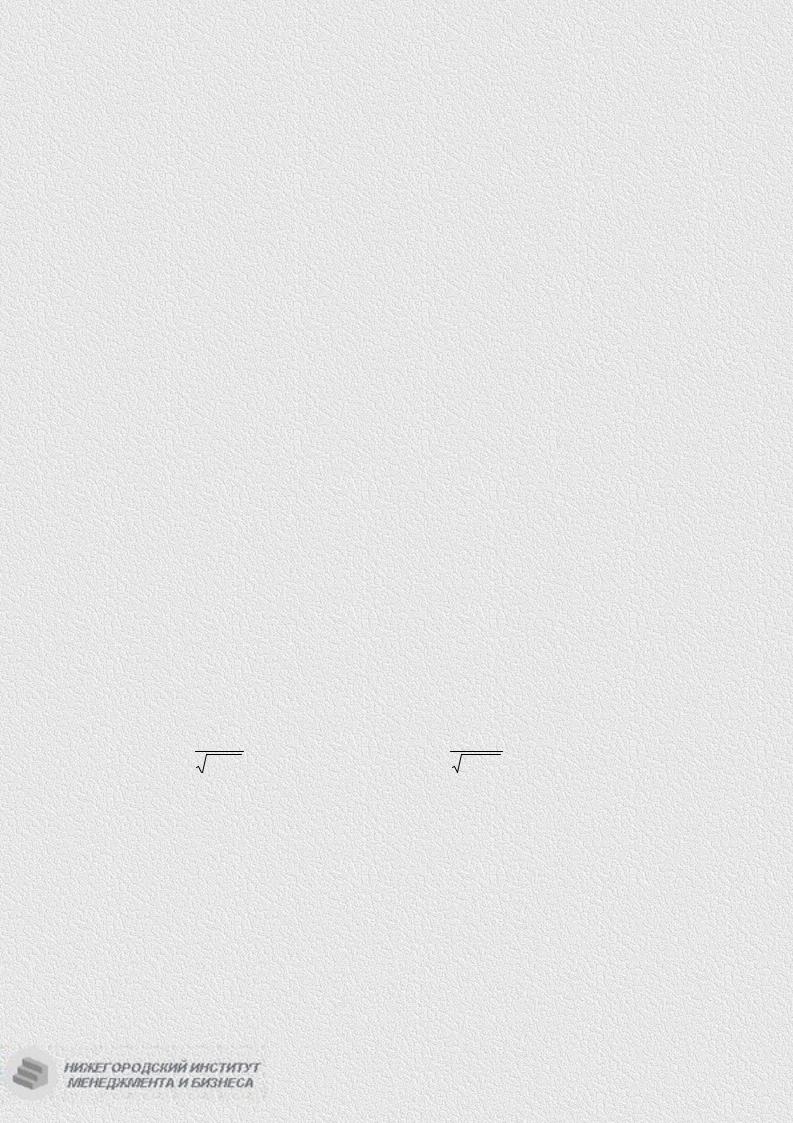
2.9. Неопределенный интеграл

Функция F(x) называется первообразной для функции f(x), если F′( x ) = f ( x )

или dF(x) = f(x)dx. Для заданной функции f(x) ее первообразная определена неоднозначно, поскольку ( F( x ) +C )′ = F′( x ) = f ( x ), где С – постоянная. Поэтому, если

функция f(x) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении F(x)+ C.

Неопределенным интегралом от функции f(x) называется совокупность всех ее первообразных. Обозначение: ∫ f ( x )dx = F( x ) +C . Здесь ∫ – знак интеграла, f(x)

– подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования.

Отыскание неопределенного интеграла называется интегрированием функции.

Свойства неопределенного интеграла

1.(∫ f ( x )dx)′ = f ( x )

2.d (∫ f ( x )dx)= f ( x )dx

3.∫dF(x) = F(x) +C

4.∫af (x)dx = a∫ f (x)dx , где а – постоянная

5.∫[f1(x) ± f2 (x)]dx = ∫ f1(x)dx ± ∫ f2 (x)dx

Таблица основных интегралов

Таблица 2.1

Формулы дифференциального исчисления

Формулы интегрального исчисления

xn+1

n

1.

∫

x

n

dx

=

xn+1

+C , n ≠ –1

1.

= x dx

d

n +1

n +1

∫dx = x + C

2.

d(ln

x

)=

1

dx

2.

∫

dx

= ln

x

+ C

x

x

3.

d(arctg x)=

1

dx

3.

∫

dx

= arctg x + C

1

+ x

2

1

+ x

2

4.

d(arcsin x) =

1

2

dx

4.

∫

dx

2

= arcsin x + C

1 - x

1 − x

5.

d(ex ) = exdx

5.

∫exdx = ex +C

6.

a

x

∫a

a

x

x

x

d

= a

dx

6.

dx =

ln a

+ C

ln a

7.

d( sin x) = cos x dx

7.

∫cosx dx = sin x + C

8.

d(- cos x) = sin x dx

8.

∫sin x dx = - cos x + C

9.

d(tg x) =

dx

9.

∫

dx

= tg x + C

cos

2

x

cos

2

x

10. d(ctg x) = −

dx

10.

∫

dx

= −ctg x + C

2

x

2

x

sin

sin

1

x - a

1

11.

∫

dx

=

1

ln

x - a

+ C

11.

d

ln

=

2

2

2

2

2a

x +a

x

−a

x

− a

2a

x

+ a

47

				Примеры и задачи
9.1. Найти интегралы:
а) ∫	dx	;	б) ∫5	x2 dx ;	в) ∫3dx .
	6
	x				x

∆ Во всех трех случаях воспользуемся табличным интегралом (1) от степенной функции, но при разных значениях n:

а) при n = – 6: ∫x−6dx =

x−5

+C = −

1

+C ;

−5

5

7

5x

2

7

б) при n =

2

:

x5

5

+C ;

∫x5 dx =

+C =

x

5

7

5

5

7

1

2

2

1

x3

3

в) при n = −

: ∫x−3 dx =

+C =

x

+C .

3

3

2

3

2

9.2. Найти интегралы:

dx

dx

1

а) ∫

;

б) ∫2x ×32 x ×53x dx ;

в) ∫

;

г) ∫(1 + x2 ) 2 x dx .

5

x

9x

2

−1

1 x

∆ а) Учитывая, что

1

=

и используя (6) при a =

1

, получаем

5x

5

5

(1

)x

dx

1

x

5

1

∫

= ∫

dx

=

ln(15)+ C

= −

+ C

5x

5

5x ln 5

б) Преобразуя интеграл, будем иметь

2250x

∫2x ×32x ×53x dx = ∫

(2 ×32 ×53 )x dx = ∫2250x dx =

+C

1

1

1

ln 2250

в) Поскольку

, то воспользуемся свойством 4 и интегра-

=

9x2 −1

9

x2 − (1

3

)2

1

лом (11) при a =

:

3

x - 13

∫

dx

∫

1

dx

1

∫

dx

1 3

1

3x −1

+C .

=

=

=

×

ln

+C =

ln

9x 2 −1

9

x 2 −(13)2

9

x 2 −

(13)2

9

2

x + 13

6

3x +1

г) Этот интеграл можно привести к формуле (2), преобразовав его так:

∫(1 + x2 )12 x dx =

1

∫(1 + x2 )12 2x dx =

1

∫(1 + x2 )12

d (1 + x2 )

2

2

Теперь переменной интегрирования служит выражение 1+х2, и относительно этой переменной получается интеграл от степенной функции. Следовательно

	∫(1 + x2 )12 x dx =	1 (1 + x2 )12 +1			+ C =	1	(1 + x2 )32	+ C
		2 12 +1				3

Метод интегрирования, основанный на применении свойств 4 и 5, называет-

ся методом разложения.

48

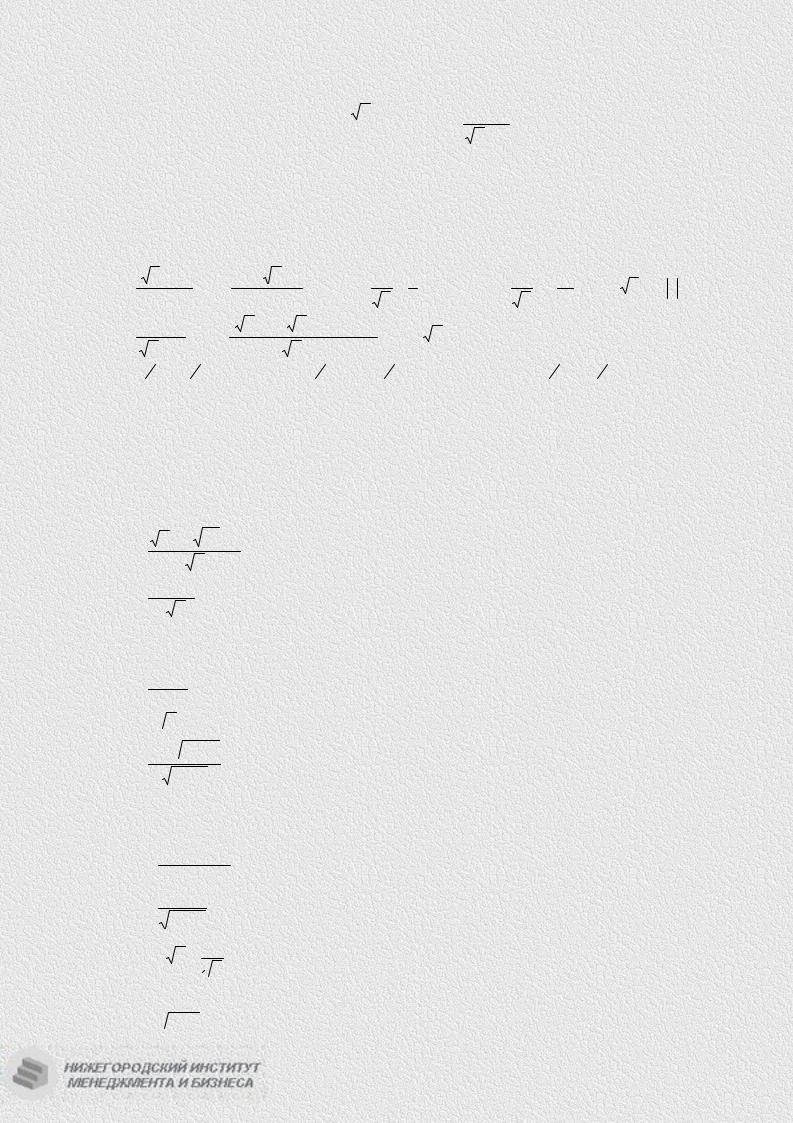
9.3. Найти интегралы:

(

x −1)2

а) ∫(2x

3

−5x

2

+ 7x −3)dx ; б)

∫

dx ; в) ∫

x2

−16

dx ; г) ∫

cos 2x

dx .

x

x + 2

sin

2

x cos

2

x

∆а) Используя свойства 4 и 5, получаем

∫(2x3 −5x2 + 7x −3)dx = 2∫x3dx −5∫x2dx + 7∫xdx −3∫dx .

К правой части применим формулу (1):

∫(2x3 −5x2 + 7x −3)dx = 2

x4

−5

x3

+ 7

x2

−3x +C =

1

x4 −

5

x3 +

7

x2 −3x +C .

2

2

(

x −1)2

4

3

2

3

б)

∫

dx =

∫

x −

2 x +1

dx =

∫

2 1

∫

∫

dx

+

∫

dx

= x −4 x +ln x +C .

+

x

x

1−

x

x

dx =

dx −2

x

x

в) ∫ x2 −16 dx =

∫( x − 2)( x + 2)(x + 4)dx = ∫( x − 2)(x + 4)dx =

x + 2

x + 2

2

8

= ∫

32

12

∫x

3

2

+ 4∫x

12

dx − 2∫xdx

−8∫dx

5

2

32

2

−8x +C .

x

+

4x

− 2x −8 dx =

dx

=

x

+

x

− x

5

3

cos 2x

cos2

x − sin

2

x

г) ∫

dx = ∫

dx

=

sin

2

x cos

2

x

sin

2

x cos

2

x

1

1

dx

dx

= −ctg x − tg x + C .

= ∫

−

dx =∫

−

∫

2

cos

2

x

sin

2

x

cos

2

x

sin

x

Найти интегралы:

3

2

9.4. ∫

x −24

x

x

+1dx

(1 −3

x)3

9.5. ∫

dx

x

x

(ex )3 +1

(ex +1)(e2 x −ex +1)

9.6. ∫

e3x +1

dx = ∫

= ∫

= ∫(e

2 x

x

+1)dx

dx

dx

−e

e

x

+1

e

x

+1

e

x

+1

9.7. ∫x2 +3 dx x2 −1

9.8. ∫x xdx

9.9. ∫2 − 1 − x2 dx

1 − x2

9.10.∫e3x ×3x dx

9.11.∫tg 2 x dx

9.12.∫ x + cos 2x dx

x2 + sin 2x

9.13. ∫	x4	5 dx
	1 + x

9.14.∫ x − 1 2 dx

x

9.15.∫x cos(x2 )dx

9.16.∫ sin x cos x dx

49

2.9.1. Метод замены переменной (метод подстановки)

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:

1)x = ϕ(t), где ϕ(t) – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид:

∫f (x)dx = ∫ f [ϕ(t)]ϕ′(t) dt

2)u = t(x), где u – новая переменная. Формула замены переменной при такой подстановке:

∫f [ψ ( x)]ψ ′( x) dx = ∫ f (u) du

9.17. Найти ∫							dx			.
						1 − 2x																																			′
∆ Положим t = 1 – 2x. Тогда x = 1																					1					1					1					1			1			1		и
																	2	−					2	t , dx = d						−		t			=			−		t dt = −			dt
																										2					2				2				2			2
						1
∫			dx	= ∫	( −		2	) dt			= −	1	∫	dt	= −	1	ln			t		+		C = −	1	ln			1 - 2x						+ C .
	1		− 2 x			t						2		t		2									2

9.18. Найти ∫cos(ax + b)dx .

∆ Имеем ax + b = t, a dx = dt и dx = 1a dt .

Следовательно, ∫cos (ax + b)dx = 1a ∫cos t dt = 1a sin t + C = 1a sin (ax + b)+ C .

9.19. Найти ∫x e−x 2 dx .

∆ Положим t = – x2. Найдем дифференциал от левой и правой части формулы

t = -x2

, используя замену переменной:

dx = d (− x2 )= (− x2 )′dx ,

то есть dt = -2x dx .

Из полученного равенства выразим x dx , тогда получим x dx = −

1

dt . Подставляя

2

это выражение в интеграл, имеем: ∫xe − x 2 dx = −

1

∫et dt = −

1

et + C = −

1

e− x 2 + C .

2

2

2

9.20. Найти ∫x2 x3 +5dx .

∆ Положим

x3 +5 = t , тогда x3 +5 = t2 . Дифференцируя обе части равенства:

2

2

2

3x

dx

= 2t dt . Отсюда x

dx =

t dt и, следовательно,

3

2 ( x3 + 5 )3 + C .

∫x2 x3 + 5 dx = ∫ x3 +

5 x2 dx = ∫t 2 t dt = 2 ∫t 2 dt =

2 t3 + C =

(2 ln x + 3)3

3

3

9

9

9.21. Найти ∫

dx .

x

dx

∆ Перепишем данный интеграл в виде ∫(2 ln x + 3)3

. Так как производная

x

выражения 2 ln x + 3 равна 2x , а второй множитель 1/х отличается от этой производной только постоянным коэффициентом 2, то нужно применить подста-

новку

2 ln x + 3 = t . Тогда 2

dx

= dt ,

dx

=

1

dt .

x

x

2

Следовательно, ∫(2 ln x + 3)3 dx

= ∫t 3

1 dt =

1

∫t 3 dt =

1 t 4

+ C =

1

(2 ln x + 3)4

+ C .

x

2

2

8

8

50

9.22. Найти интегралы:

а) ∫		dx		; б) ∫		2dx	2 , a > 0.
	x	2	2		a
		+ a				− x

∆Эти интегралы с помощью подстановки x = at сводятся к табличным (3) и

(4)соответственно.

∫

dx

=

(x = at, dx = a dt)=

1

∫

dt

=

1

(arctg t + C)

=

1

arctg

x

+ C

x

2

+ a

2

a

t

2

+1

a

a

a

∫

a

2dx

2

= ∫

dt

2 = arcsin t + C = arcsin

x

+ C

− x

1 − t

a

9.23. Найти интегралы ∫tg x dx ,

∫ctg x dx .

dt

∆ ∫tg x dx = ∫

sin x

dx = (cos x = t,- sin x dx = dt)= −∫

= −ln

t

+ C = −ln

cos x

+ C . Ана-

cos x

t

логичное вычисление с заменой sin x = t

дает для второго интеграла выражение

∫ctg x dx = ln

sin x

+ C .

2dx

9.24. Найти интеграл ∫

x

2 .

+ a

∆ Применим подстановку x = a Sh t , dx = a Ch t dt , учитывая, что Ch2t – Sh2t = 1,

получим

dx

a Ch t dt

Ch t dt

∫

= ∫

= ∫

= t

+ C .

x

2

+ a

2

a

Sh

2

Ch t

t +1

1

x

Выразим t через х. Имеем, учитывая Sh t =

(et

− e−t ),

2

= et

−e−t . Обозначим

2

a

x

1

et

= y,

тогда 2

= y −

и мы получаем квадратное уравнение относительно у:

a

y

y2

− 2

x

y −1 = 0 .

Решая это квадратное уравнение,

получаем

y = x +

x2 +1

или

a

a

a2

e

t

=

x +

x2 + a2

t

для

a

. Мы взяли только положительное решение,

так как e > 0

всех t. Логарифмируя, получаем окончательно t = ln x +

x2

+ a 2

− ln a . Следова-

тельно ∫

x

2dx

2

= ln x +

x2

+ a 2 + C .

+ a

Найти интегралы:

9.25.

∫

x4 dx

9.29.

∫

e

x

dx

9.33.

1 +

x

dx

x10 − 2

x

x

9.26. ∫

x dx

9.30. ∫

ln x

dx

9.34.

∫

4

5 + 3 ln(sin x) ctg x dx

x4 + 2x2

+5

x

9.35.

dx

9.27. ∫

e2 x

dx

9.31. ∫

e

2 x−1

dx

∫(x −7)

x

e4 x −5

9.28. ∫

1x−dxx2

9.32. ∫

2x −

1

9.36. ∫

x2 dx

x

4dx

2 −3x3

x

−1

51