01_Физические_основы_механики

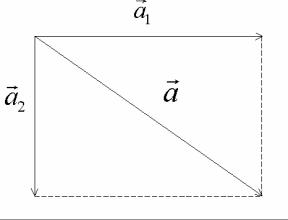
Рис. 6. Проекция вектора на ось

Проекцией вектора а на ось l называется алгебраическая величина, равная произведению модуля вектора на угол между направлениями вектора и оси

al = a cosϕ.

6. Разложение вектора на составляющие

Всякий вектор можно представить в виде суммы двух или более других векторов. Например, a = a1 + a2 .

Рис. 7. Разложение вектора на составляющие

Векторы ar1 и a2 называются составляющими вектора a

или компонентами вектора. Такое представление называется

разложением вектора на составляющие.

6. Скалярное произведение векторов

Скалярным произведением двух векторов называется скаляр, равный произведению модулей этих векторов на косинус угла между векторами

ar b = ab cosϕ , (ar,b )= ab cosϕ .

10

Рис. 8. Скалярное произведение

Умножим вектор a сам на себя скалярно

a a = a a cos 0 = a2 .

Квадрат вектора равен квадрату модуля этого вектора.

Рис. 9. Векторное произведение

11

7. Векторное произведение векторов

Векторнымr произведением векторов a и b называется век-

тор c , удовлетворяющий следующим условиям: 1. Вектор равен cr = ar×b = [ar, b] ;

r 2.rМодуль вектора c равен произведению модулей векторов a и b на синус угла между ними c = absinϕ ;

3. Векторr rc перпендикулярен плоскости, в которой лежат

векторы a и b ;

4. Из конца вектора c поворот от первого сомножителя ко второму сомножителю по кратчайшему пути должен быть виден происходящим против часовой стрелки.

Декартова система координат

Декартова прямоугольная система координат образована тремя взаимно-перпендикулярными, пересекающимися в одной точке O жесткими стержнями. Каждый стержень, с нанесенными на него масштабными метками, образует координатную ось Ox,Oy,Oz . Стрелки указывают положительное направление оси.

Точка пересечения осей O называется началом системы коорди-

нат.

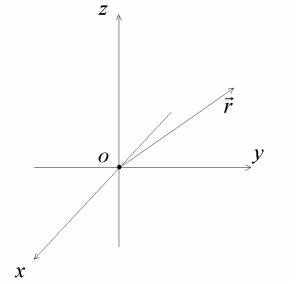
Возьмем некоторуюr точку М и проведем в нее из начала коор-

динат вектор r .

Вектор, проведенный из начала координат в некоторую точку,

называется радиус-вектором этой точки:		rM = r. Конец радиус-
вектора r совпадает с данной точкой.
Обозначим координаты	точки М: x, y, z .		Модуль радиус-
вектора оказывается равен	r = x2 + y 2	+ z 2	. Величины x, y, z

есть координаты конца радиус-вектора или проекции радиусвектора на оси координат. Обозначим единичные векторы (ор-

ты) декартовых осей erx = i , ery = j,erz = k . Радиус-вектор точки

12

с координатами x, y, z можно представить так: rr = xi + yj + zk.

Векторы i , j, k взаимно		перпендикулярны. Это означает,		что
i j = 0, j k = 0, i k = 0.		В то же время очевидно,		что
i i =1, j j =1, k k =1.

Рис. 10. Декартова система координат

Функция, производная, интеграл

Если каждому значению величины x можно сопоставить значение величины y , то y и x связаны функциональной зависи-

мостью или y есть функция аргумента x : y = f (x).

Возьмем два значения аргумента x и (x + ∆x). Величина ∆x

называется приращением аргумента x . Вычислим приращение функции

∆f = f (x + ∆x)− f (x).

13

Составим отношение

∆∆fx =

Значение отношения ∆f

∆x

f(x + ∆x) − f(x) .

∆x

в общем случае зависит от значения

∆x . Будем неограниченно уменьшать приращение ∆x . При этом значение отношения сначала будет изменяться достаточно сильно, затем изменение значения может уменьшаться, приближаясь (стремясь) к нулю. Само отношение при этом стремится к производной

функции по аргументу

	lim	f(x + ∆x) − f(x)		= df .
		∆x
	∆x → 0			dx
	Производной функции f по аргументу x называется предел,

к которому стремится отношение приращения функции df к

приращению аргумента dx при неограниченном уменьшении приращения аргумента.

Величины dx , df называются элементарными или бесконечно малыми приращениями аргумента x и функции f . Разобьем некоторый интервал (xa , xb ) на очень большое число n

очень маленьких интервалов dx . Пронумеруем все интервалы dx и составим сумму

f(x1 )dx1 + f(x2 )dx2 + ... + f(xi )dxi + ...

n

+ f(xn )dxn = ∑ f(xi )dxi ,

i=1

где f (xi ) – значение функции для аргумента xi , взятого в любой точке внутри интервала dxi . Вычислим сумму при неограниченном уменьшении dx → 0 и, соответственно, при n → ∞:

14

n	xb
lim∑ f (xi )dxi =∫ f (x)dx.
dx→0 i=1	xa

Предел, к которому стремится указанная сумма, называется

определенным интегралом от функции f (x).

Приращение и убыль величины

Пусть имеется функциональная зависимость f (t), где t –

время. Выберем два момента времени:		tН – начальный момент
времени, tK	– конечный момент времени.		Соответственно,
fH = f (tH ) – начальное значение функции,			fK = f (tK ) – ко-
нечное значение функции.		f называется разность
Приращением некоторой величины

конечного и начального значения этой величины

∆f = fK − fH .

Убылью некоторой величины f называется разность начального и конечного значения этой величины

− ∆f = fH − fK .

Единицы физических величин

Будем применять международную систему единиц или систему СИ. В этой системе имеются основные единицы.

Длина – метр – м. Масса – килограмм – кг. Время – секунда – с.

Температура – Кельвин – К. Сила тока – Ампер – А. Количество вещества – моль.

Из основных единиц можно получить производные единицы системы СИ. Например,

15

	скорость=	метр		=	м	,	сила =	килограмм	=	кг	, Н.
		секунда			с			метр секунда2		м с2

Часто применяют десятичные множители и связанные с ними приставки.

Например, 100 нКл = 100·10-9 Кл = 10-7 Кл = 0,1·10-6 Кл = 0,1

мкКл. Кроме основных и производных единиц системы СИ используют внесистемные единицы физических величин.

Например, 1 минута = 60 с,1 тонна = 1000 кг, 1 электронвольт = = 1,6 · 10-19 Дж.

Таблица 1

Десятичные множители и приставки в системе единиц СИ

множитель	обозначение	наименование
1012	Т	Тера
109	Г	Гига
106	М	Мега
103	к	кило
10−3	м	милли
10−6	мк	микро
10−9	н	нано
10−12	п	пико

Вычисления и запись результата

При вычислении в формулу необходимо подставлять величины, выраженные через основные единицы системы СИ. Ответ нужно записывать в следующем виде, например:

P =3,75 10−5 Па, где

P – обозначение величины, 3,75 – три десятичные цифры, 10 – десятичный множитель,

5 – порядок десятичного множителя, «–» – знак порядка, Па – наименование единицы величины.

16

МЕХАНИКА

Механика – это раздел физики, изучающий перемещение тел друг относительно друга. Движение тел в механике считают быстрым или медленным, сравнивая скорость движения со скоростью света в вакууме, которая равна

c =3 108 мс .

Движение считается быстрым, если скорость движения сравнима со скоростью света. Движение считается медленным, если

скорость движения много меньше, чем скорость света V << c . Механика, изучающая медленные движения, называется классической или ньютоновской. Механика, изучающая быстрые движения, называется релятивистской.

Объектом механики может быть любое физическое тело. Однако всякое тело обладает многими и разнообразными свойствами и связями с другими телами. Учесть все свойства и связи сложно или невозможно. Поэтому обычно ограничиваются рассмотрением лишь некоторых, важных в рассматриваемом явлении, свойств и связей. Изучение лишь некоторых свойств реального объекта означает замену этого объекта некоторой идеализацией, называемой моделью. Простейшая модель реального тела, которая использует-

ся в механике – это материальная точка (частица).

Материальной точкой (частицей) называют тело, размерами которого можно пренебречь в условиях данной задачи.

Глава 1. Кинематика материальной точки и твердого тела

Кинематика – раздел механики, изучающий движение тел без учета причин возникновения и изменения движения.

1.1. Основная задача кинематики для материальной точки

Тело, относительно которого определяется положение остальных тел, называется телом отсчета. Для определения положения частицы относительно тела, с ним связывают систему координат, например, декартову. Для описания движения необходимо

17

не только определять положение частицы, но и фиксировать соответствующие моменты времени. Для этой цели используют специальное устройство – часы.

Тело отсчета, связанные с ним система координат и часы образуют систему отсчета. Пусть положение частицы определяется координатами x, y, z . Вследствие движения координаты изме-

няются с течением времени. Это можно записать следующим образом:

x= x(t), y = y(t), z = z(t).

Впроцессе движения частицы ее координаты x, y, z являются

функциями времени t . Положение частицы можно задать радиусвектором

r = r[x(t), y(t), z(t)]= r (t).

Данные уравнения в общем виде описывают движение материальной точки. Основная задача кинематики заключается в нахождении явного выражения этих уравнений.

1.2. Путь, перемещение материальной точки

Пусть в некоторый момент времени t частица находилась в точке 1, положение которой определяется радиус-вектором r1 (t) . Спустя промежуток времени ∆t >0 , в момент времени (t + ∆t) частица оказалась в точке2, срадиус-вектором rr2 (t + ∆t) .

Линия, которую материальная точка описывает при своем движении, называется траекторией движения. Расстояние, отсчитанное вдоль траектории, называется длиной пути или путем, которой частица проходит за время движения. В системе СИ

единица измерения пути – метр. Обозначение пути ∆s, s .

Точку 1 назовем начальным положением частицы, а точку 2 конечным положением частицы. Вектор, проведенный из начального положения частицы в ее конечное положение называется

вектором перемещения или перемещением ∆r , м.

Очевидно, что ∆s ≥ ∆rr. Из рисунка видно, что

∆r = r (t + ∆t) − rr(t).

18

dr = r (t + dt) − rr(t).

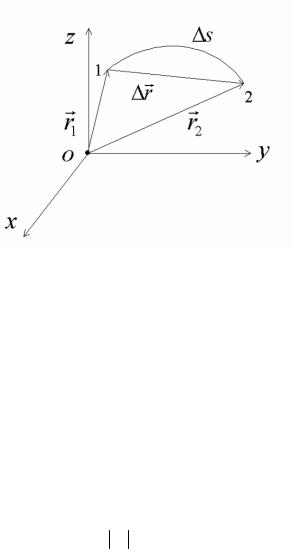
Выражение в правой части имеет смысл разности конечного значения и начального значения радиуса-вектора. Такая разность называется приращением радиус-вектора. Вектор перемещения частицы за некоторый промежуток времени равен приращению радиус-вектора частицы за этот промежуток времени.

Рис. 1.1. Путь, перемещение материальной точки

1.3. Элементарный путь, элементарное перемещение

Будем неограниченно уменьшать интервал времени движения ∆t . При ∆t <<t интервал времени называется бесконечно малым или элементарным и обозначается так: dt . За бесконечно малый интервал времени dt частица проходит бесконечно малый путь

ds и совершает бесконечно малое перемещение dr , которое равно

Отметим следующие важные свойства. В пределе, при dt →0 , вектор dr сливается с участком траектории ds , причем вектор dr направлен по касательной к траектории и модуль век-

тора dr равен длине элементарного пути ds : drv = ds.

19