01_Физические_основы_механики

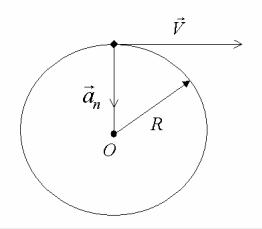
Наконец, если одновременно существуют и тангенциальное и нормальное ускорения, то скорость изменяется как по величине, так и по направлению.

Если частица движется по криволинейной траектории, то мгновенная скорость в разных точках траектории имеет различное направление, т.е. направление скорости в процессе движения изменяется. Следовательно, в этом случае имеется нормальное ускорение. Движение по криволинейной траектории происходит с нормальным ускорением, отличным от нуля.

Рис. 1.10. Центростремительное ускорение

При движении по окружности нормальное ускорение, направленное к центру окружности, называют также центростреми-

тельным ускорением.

1.9. Уравнение кинематики для материальной точки

Пусть в нулевой (начальный) момент времени частица находится в точке 1 с радиус-вектором r0 : t = 0 , r0 = r (0) . За время t

после начала движения частица перемещается вдоль некоторой траектории в точку 2 с радиусом-вектором r (t) . Разобьем интер-

вал времени от 0 до t на очень большое число элементарных интервалов

30

dt1 ,dt2 ,...,dti ,...,dtn .

За каждый такой интервал частица совершает элементарные перемещения

dr1 ,dr2 ,...,dri ,...,drn .

Результирующее перемещение частицы за все время t равно

∆rr = ∑n drri .

i=1

Для каждогоэлементарного интервала времени dt справедливо

r		drr
V	=	i	,
i		dt

где Vi – мгновенная скорость, постоянная в течение dti . Отсюда

drri =Vi dti , ∆rr = ∑n Vri dti .

i=1

При n →0,dti →0 сумму можно заменить определенным интегралом:

n	r	t	r	∆rr	t	r
lim∑Vi dti = ∫Vdt,					= ∫Vdt.
dti →0 i=1		0			0

31

Рис. 1.11. Вычисление вектора перемещения

Из рисунка видно, что r0 +∆r = r (t) . Следовательно,

			t	r
	rr(t) = rr0 + ∫Vdt .
	0
Теперь необходимо найти зависимость V (t) . Пусть в началь-
ный момент времени мгновенная скорость равна V0 . Для каждого
интервала dti запишем
ar	=	dVi	, dV = ar		dt	,
i			i	i	i
		dti

где dVi – приращение мгновенной скорости за время dti , ari –

ускорение в течение этого интервала времени. Очевидно, что по истечении dt1 имеем

V1 =V0 + ar1dt1 .

По истечении промежутка времени dt2 :

V2 =V1 + ar2 dt2 =V0 + ar1dt1 + ar2 dt2 .

Наконец, в момент времени t , скорость равна:

r	r	n	r	r	t	r
V (t) =V0		+ ∑ai dti =V0			+ ∫adt .
		i=1			0

1.10.Уравнения кинематики для равнопеременного движения

Движение материальной точки называется равнопеременным, если ускорение остается постоянным по величине и направлению с течением времени: a =const. Вычислим V (t) и r (t) .

r	r	t	r	r	rt	r	r
Запишем V (t) =V0		+ ∫adt =V0			+ a∫dt =V0		+ at ,
		0			0
				32

r	r	t r	r	r	r	t	rt	r	r	art	2
r (t) = r0		+ ∫(V0	+ at)dt = r0		+V0	∫dt + a∫tdt = r0			+V0t +	2	.
Итак,		r 0		r	r	0 r	r0	art 2
	V (t) =V			+ at ,	r (t)	= r	+V t +		. Спроецируем
			0			0	0	2

равенства на оси декартовой системы координат. Получим:

Vx =V0x +axt, Vy =V0 y +ayt,

Vz =V0 z +azt ,

ax = const, ay = const, az

= const,

x(t) = x

+V

t +

a

x

t

2

0

,

0 x

2

a

t2

y(t) = y

o

+V

t +

y

,

0 y

2

2

z(t) = z

+V

t +

a

t

0

z

.

0 z

2

Здесь, V0 x ,V0 y ,V0 z – проекции скорости частицы в нулевой

момент времени, ax ,ay , az – проекции ускорения

частицы,

x0 , y0 , z0 – координаты частицы в

нулевой момент

времени,

x(t), y(t), z(t) – координаты частицы в момент времени t .

1.11. Уравнения кинематики для равномерного движения

Движение материальной точки называется равномерным, если вектор мгновенной скорости остается постоянным по величине и

направлению с течением времени: V = const . Запишем ar = ddtV = 0 .

При равномерном движении ускорение равно нулю a = 0 . Из предыдущего параграфа можно получить

33

V (t) =V0 =V = const ,

rr(t) = rr0 +Vt, x(t) = x0 +V xt, y(t) = y0 +Vy t, z(t) = z0 +Vz t, Vx = const,Vy = const,Vz = const.

1.12. Прямолинейное равнопеременное движение

Пусть частица движется, например, вдоль оси x , так что изменяется только координата x. В этом случае достаточно записать уравнения для проекций на ось x

	Vx =V0 x + ax t, x(t) = x0 +V0 x t +	a	t 2
		x		.
		2

Часто индекс «x» не пишут, и при этом выражения принимают

следующий вид: V =V + a t ,		x(t) = x	+V t +	a t2	.
0		0	0	2

Рис. 1.12. Движение вдоль оси х

1.13. Вычисление пути

Рассмотрим движение частицы вдоль траектории. За элементарный промежуток времени dt1 , частица пройдет элементарный путь ds1 , за промежуток dt2 пройдет путь ds2 и т.д. Длина пути, пройденного частицей за время t , равна

34

n

s= ∑dsi .

i=1

Запишем для i-го участка

V= dsi ,

idti

где Vi – модуль мгновенной скорости на i-м участке пути. Далее

n

dsi =Vi dti , s = ∑Vi dti .

i=1

В пределе при dt → 0 получаем

s = ∫t Vdt ,

0

где V – есть модуль мгновенной скорости. Пусть движение происходит с постоянной по величине мгновенной скоростью

V = const , тогда

s = ∫t	Vdt =V ∫t	dt =Vt, s =Vt.
o	0

Рассмотрим движение частицы вдоль оси x , при котором направление скорости частицы не изменяется. Пусть движение происходит с постоянным ускорением. Запишем:

x(t) = x0 +V0 xt + at22 .

В этом случае путь равен расстоянию между точками с координатами x(t) и x0 :

s(t) = x(t) − x0	=V0t +	at 2	,	s(t) =V0t +	at	2	.
		2			2

35

Рис. 1.13. Вычисление пути при прямолинейном движении

1.14. Вращение твердого тела вокруг неподвижной оси

Абсолютно твердым телом (твердым телом) называется система материальных точек, расстояния между которыми остаются неизменными.

Движение твердого тела, при котором все его точки описывают окружности, центры которых лежат на некоторой прямой, на-

зывается вращением вокруг неподвижной оси.

36

Рис. 1.14. Движение материальной точки по окружности

Пусть при вращении твердого тела точка М движется по окружности радиуса R с центром O, лежащим на оси вращения O1O2. Пусть за элементарный интервал времени dt радиус R, соединяющий точку М с центром окружности повернулся на элементарный угол dφ, который называется элементарным углом поворотатела.

Введем вектор dϕ , модуль которого равен элементарному углу поворота, выраженному в радианах: dϕr = dϕ, рад. Направим

вектор dϕr вдоль оси вращения так, чтобы его направление и направление вращения тела были связаны т.н. правилом правого буравчика: направление вектора dϕ совпадает с направлением

поступательного движения конца правого буравчика, если ось буравчика расположить вдоль оси вращения, а рукоятку поворачи-

37

вать в направлении вращения тела. Вектор dϕ называется век-

тором элементарного поворота.

Угловой скоростью называется вектор, равный отношению вектора элементарного поворота к длительности элементарного промежутка времени, в течение которого произошел поворот

ωv = ddtϕ .

Направление вектора ω совпадает с направлением вектора dϕr. Следовательно, вектор ω связан с направлением вращения

тела правилом правого буравчика. Запишем для модуля угловой скорости

ωr

=

|dϕ|

,

ωr

=ω =

dϕ

,

рад

.

dt

dt

с

Возьмем точку Р, лежащую на одном радиусе с точкой М, но ближе к оси вращения. За время dt , точки М и Р проходят разный путь, но при этом вместе с радиусом оси поворачиваются на один и тот же угол dϕ . Следовательно, обе точки имеют одну и ту же

угловую скорость.

Все точки твердого тела, вращающегося вокруг неподвижной оси, имеют одну и ту же угловую скорость

ω = const, ω = const.

Угловым ускорением называется вектор, равный отношению элементарного приращения вектора угловой скорости к элементарному промежутку времени, за который произошло это приращение

εr = dω рад dt , с2 .

1.15.Проекция угловой скорости и углового ускорения на ось вращения

Обозначим ось вращения O1O2 как ось z , причем положительное направление оси z совпадает с направлением вектора угловой скорости.

Найдем проекцию вектора ω на ось вращения z :

38

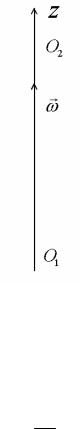
ωz =

ωr

cos 0 =

ωr

=

dϕr

=

dϕ

.

dt

dt

Рис. 1.15. Ось вращения z

Пусть вектор углового ускорения ε направлен вдоль оси вращения z . Направление ε может совпадать с направлением вектора угловойr скорости ω или может быть противоположным вектору ω :

ωz = ddtϕ .

Запишем				dωr
		ε
			z	=			=
				dt		z
=	[ωr	(t + dt)]z −[ωr(t)]z
				dt

[ωr(t + dt)		−ωr(t)]	z	=
	dt
							,
=	ωz (t + dt) −ωz (t)				=	dωz
		dt				dt

39